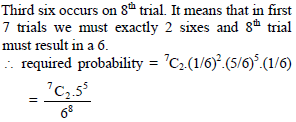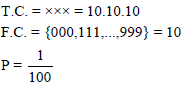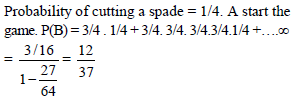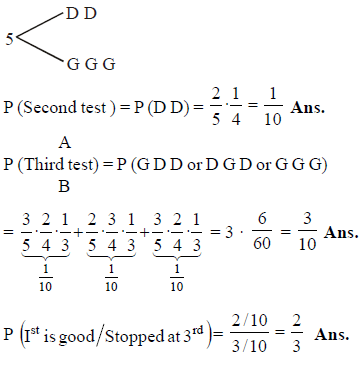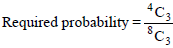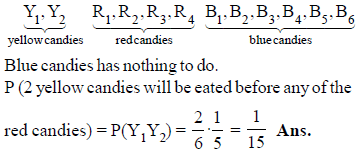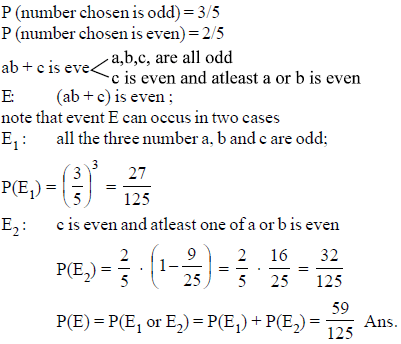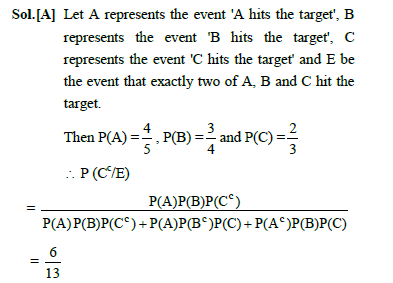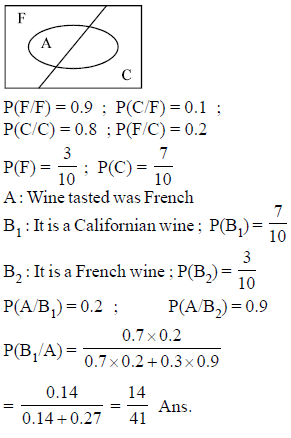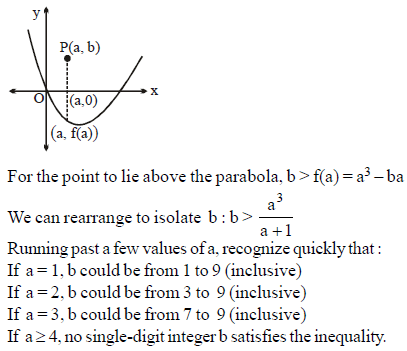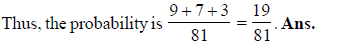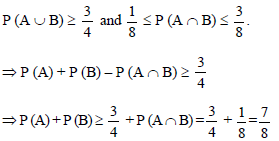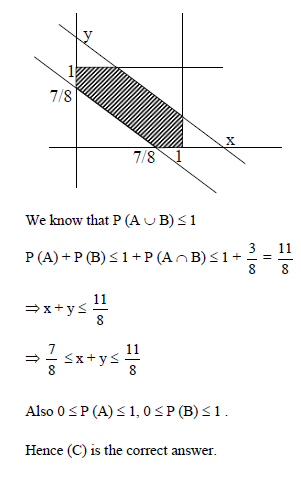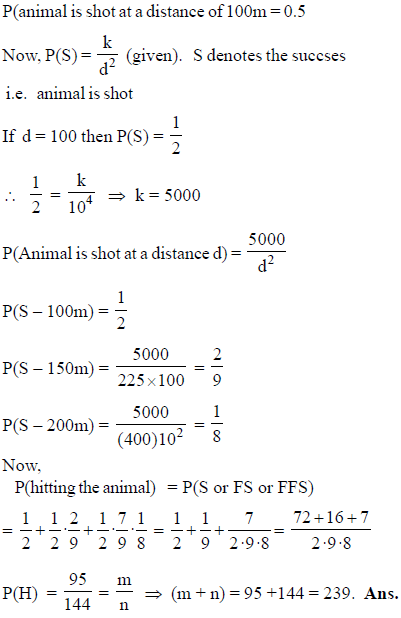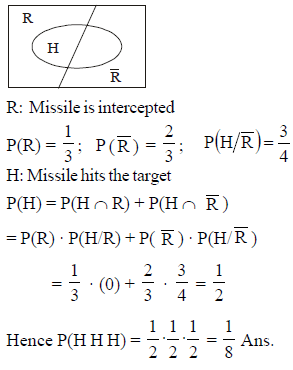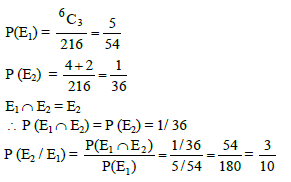Probability - 1 - JEE MCQ
30 Questions MCQ Test - Probability - 1
If the probability of solving a problem by three students are 1/2,1/3 and 1/4 then probability that the problem will be solved-
Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is-
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is
In a binomial distribution, if the probability of at least one success is greater than or equal to 9/10, then n is greater than :
Three numbers are chosen at random without replacement from {1, 2, 3, ....8}. The probability that their minimum is 3, given that their maximum is 6, is :
Consider the system of equations ax + by = 0, cx + dy = 0, where a, b, c, d ∈ {0, 1}
Statement-1 : The probability that the system of equations has a unique solution is 3/8.
Statement-2 : The probability that the system of equations has a solution is 1.
A fair dice is tossed eight times. Probability that on the eighth throw a third six is observed is -
The last three digits of a telephone number beginning with 135 _ _ _ have been erased. The probability that the erased digits will be all identical is -
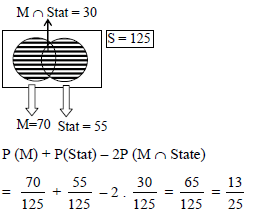
In a class of 125 students 70 passed in Mathematics, 55 in Statistics and 30 in both. The probability that a student selected at random from the class has passed in only one subject is -
A, B, C in order cut a pack of cards replacing them after each cut, on the condition that the first who cuts a spade shall win the prize. Then the probability of B to win the prize is-
A box contains 5 radio tubes of which 2 are defective. The tubes are tested one after the other until the 2 defective tubes are discovered. The probability that the process stopped on the third test, is
There are 4 white and 4 black balls in a bag and 3 balls are drawn at random. If balls of same colour are identical, the probability that none of them is black, is-
A quadratic equation is chosen from the set of all the quadratic equations which are unchanged by squaring their roots. The chance that the chosen equation has equal roots is :
A jar contains 2 yellow candies, 4 red candies, and 6 blue candies. Candies are randomly drawn out of the jar one-by-one and eaten. The probability that the 2 yellow candies will be eaten before any of the red candies are eaten, is
If a, b and c are three numbers (not necessarily different) chosen randomly and with replacement from the set {1, 2, 3, 4, 5}, the probability that (ab + c) is even, is
A can hit a target 4 times in 5 shots, B three times in 4 shots and C twice in 3 shots. They fire a target if exactly two of them hit the target then the chance that it is C who has missed is
India play two matches each with West Indies and Australia. In any match the probabilities of India getting 0, 1 and 2 points are 0.45, 0.05 and 0.50 respectively. Assuming that the outcomes are independent, the probability of India getting at least 7 points, is -
A letter is known to have come from either
TATANAGAR or CALCUTTA. On the
envelope, just two consecutive letters TA are
visible . The probability that the letter has come
from CALCUTTA is
Mr. Dupont is a professional wine taster. When given a French wine, he will identify it with probability 0.9 correctly as French, and will mistake it for a Californian wine with probability 0.1. When given a Californian wine, he will identify it with probability 0.8 correctly as Californian, and will mistake it for a French wine with probability 0.2. Suppose that Mr. Dupont is given ten unlabelled glasses of wine, three with French and seven with Californian wines. He randomly picks a glass, tries the wine, and solemnly says : "French". The probability that the wine he tasted was Californian, is nearly equal to
Suppose a and b are single-digit positive integers chosen independently and at random. The probability that the point (a, b) lies above the parabola y = ax2 – bx, is
A hunter fires a shot at an elk from a distance of 100m, and hits it with a probability of 0.5. If he does not hit it on the first shot, he fires a second shot from a distance of 150m. If he does not hit the elk in this case, he fires the third shot from a distance of 200m. If the probability of a hit is inversely proportional to the square of the distance, then the probability of hitting the elk can be expressed in lowest rational as m/n. Find (m + n).
When a missile is fired from a ship, the probability that it is intercepted is 1/3. The probability that the missile hits the target, given that it is not intercepted is 3/4. If three missiles are fired independently from the ship, the probability that all three hits the target, is
A number is picked up at random from the number {1, 2,.........1000}. The probability that the number is of the form mn (m, n > 1) is
A card is drawn & replaced in an ordinary pack of 52 playing cards. Minimum number of times must a card be drawn so that there is atleast an even chance of drawing a heart, is
A die is rolled three times. Let E1 denotes the event of getting a number larger than the previous number each time and E2 denotes the event that the numbers (in order) form an increasing AP then
The chance that the vowels are separated in an arrangement of the letters of the word “HORROR” is :
A dice is rolled three times, the probability of getting a large number than the previous number each time is