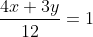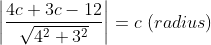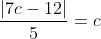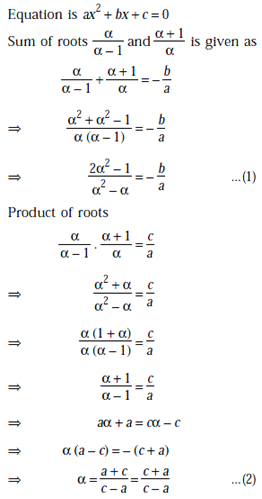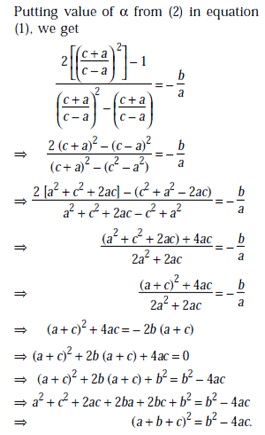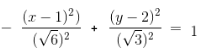BITSAT Mock Test - 2 - JEE MCQ
30 Questions MCQ Test - BITSAT Mock Test - 2
If a source emitting waves of frequency f moves towards an observer with a velocity v/4 and the observer moves away from the source with a velocity v/6. The apparent frequency as heard by the observer will be
(v = Velocity of sound)
(v = Velocity of sound)
If a vector  is perpendicular to the vector
is perpendicular to the vector 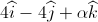 , then the value of α is
, then the value of α is
 is perpendicular to the vector
is perpendicular to the vector 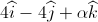 , then the value of α is
, then the value of α isA cube is subjected to a uniform volume compression. If the side of the cube is decreased by 2%, then the bulk strain is
The length of a wire of a potentiometer is 100 cm and the emf of its standard cell is E volt. It is employed to measure the emf of a battery whose internal resistance is 0.5 W. If the balance point is obtained at l = 30 cm from the positive end, then the emf of the battery is
The velocities of light in two different mediums are 2 x 108 ms-1 and 2.5 x 108 ms-1 respectively. The critical angle for these mediums is
A toy of mass M1 is pulled along a horizontal frictionless surface by rope of mass M2. A force F is applied to the free end of the rope. The force exerted on the toy is:
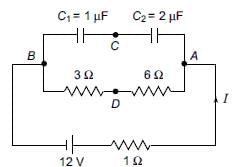
What is the potential difference between points C and D in the circuit shown in the figure?
If the acceleration due to gravity is 'g' on the surface of Earth, then the value of acceleration due to gravity at a height of 32 km above the surface of Earth is (radius of Earth = 6400 km)
At 25°C, the dissociation constant of a base, BOH, is 1.0 × 10-12. The concentration of hydroxyl ions in 0.01 M aqueous solution of the base would be
The de-Broglie wavelength of the electron in the ground state of hydrogen atom is
(KE = 13.6 eV and 1 eV = 1.602 x 10-19 J)
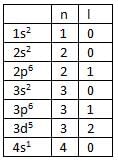
Consider the ground state configuration of Cr atom (Z = 24). The total numbers of electrons with azimuthal quantum numbers l = 1 and l = 2, respectively, are
Ferrous oxide forms a lattice structure in which the length of edge of the unit cell is 5 
Directions: In this question, the second figure of the problem figures bears a certain relationship to the first figure. Similarly, one of the figures in the answer figures bears the same relationship to the third problem figure. You have to select the figure from the set of answer figures which would replace the sign of question mark (?).
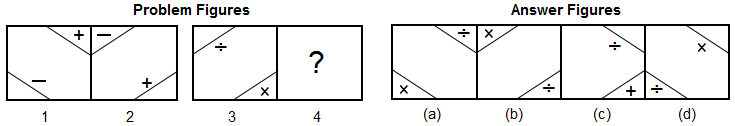
With which of the following statements is the author most likely to disagree?
a. Preservation of wetlands is necessary in the interest of biodiversity and long-term survival of humanity.
b. Tidal wetlands are as prone to human degradation as the inland non-tidal wetlands.
c. Awareness about the need to protect wetlands has not filtered across the general populace.
Directions: There is some relationship between the two terms to the left of the sign (: :). The same relationship exists between the two terms to its right, out of which one is missing. Find the missing one from the given alternatives.
acE : bdF : : fhJ : ?
Directions: Select the phrase/connector from the given three options which can be used to form a single sentence from the two sentences given below, implying the same meaning as expressed in the statement sentences.
Frequent elections impose a huge burden on a nation's human resources and also impede the development process. The president of the country has proposed the concept of 'one nation, one election'.
a. However the frequent elections...
b. In lieu of huge burden imposed...
c. As the development process is impeded...
One ticket is selected at random from 100 tickets numbered 00, 01, 02, ….., 98 and 99. If X and Y denote the sum and the product of the digits on the tickets, respectively, then P(X = 9|Y = 0) is equal to
If 


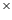 (
(






If the coefficient of correlation between x and y is 0.28, covariance between x and y is 7.6 and variance of x is 3, then the SD in y-series is
A GP consists of an even number of terms (all terms being different). If the sum of all the terms is five times the sum of the terms occupying odd places, then the common ratio will be
The equation of the circle which touches the coordinate axes and the line 
If the roots of the equation ax2 + bx + c = 0 are of the form 
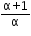 , then the value of (a + b + c)2 is
, then the value of (a + b + c)2 is
The value of eccentricity for the hyperbola x2 - 2y2 - 2x + 8y - 1 = 0 is


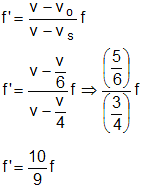
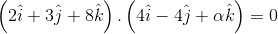
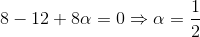

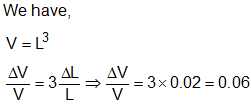
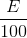 V/cm
V/cm , l = 30 cm
, l = 30 cm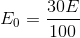
 up to correct significant figures is equal to
up to correct significant figures is equal to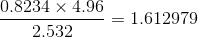
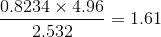
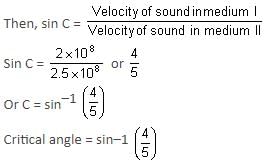
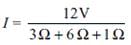
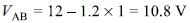
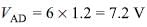
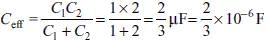
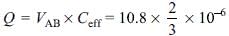
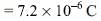
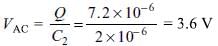
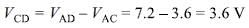
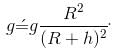
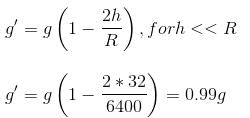



 Kb =
Kb = 
 and [BOH] = 0.01 M
and [BOH] = 0.01 M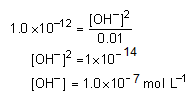
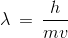






 cm
cm V = (5 × 10-8)3 cm3
V = (5 × 10-8)3 cm3
 4
4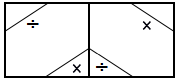



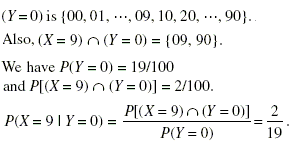
 is equal to
is equal to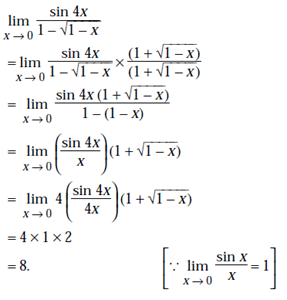

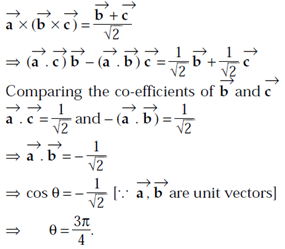
 , then z satisfies
, then z satisfies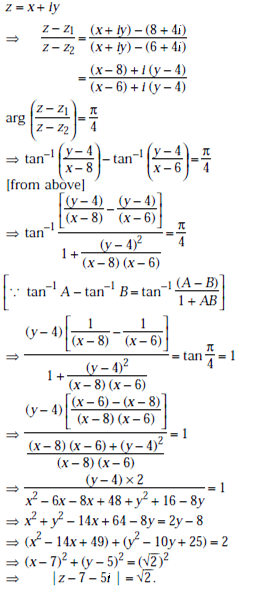
 , then
, then  is equal to
is equal to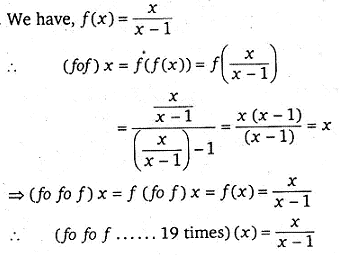
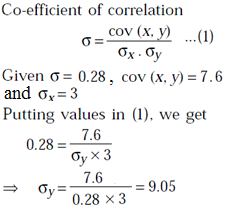
 is
is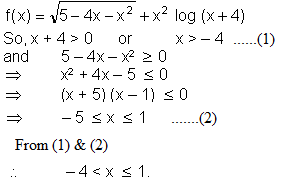
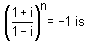
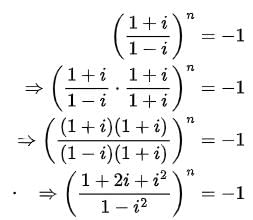
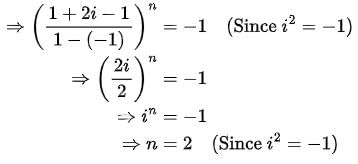
 = 5[a + ar2 + ... + ar2n - 2]
= 5[a + ar2 + ... + ar2n - 2] = 5a[1 + r2 + ... + r2n - 2]
= 5a[1 + r2 + ... + r2n - 2]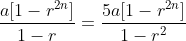
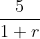
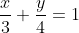 ...(2)
...(2)