Explore Exams
Login Signup
Sign in Open App
CAT Exam  >  CAT Tests  >  Test: Venn Diagrams- 1 - CAT MCQ

Test: Venn Diagrams- 1 - CAT MCQ


Test Description

10 Questions MCQ Test - Test: Venn Diagrams- 1

Test: Venn Diagrams- 1 for CAT 2025 is part of CAT preparation. The Test: Venn Diagrams- 1 questions and answers have been prepared according to the CAT exam syllabus.The Test: Venn Diagrams- 1 MCQs are made for CAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Venn Diagrams- 1 below.
Solutions of Test: Venn Diagrams- 1 questions in English are available as part of our course for CAT & Test: Venn Diagrams- 1 solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test: Venn Diagrams- 1 | 10 questions in 20 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
Test: Venn Diagrams- 1 - Question 1
Save

There are 3 clubs A, B & C in a town with 40, 50 & 60 members respectively. While 10 people are members of all 3 clubs, 70 are members in only one club. How many belong to exactly two clubs?

Detailed Solution for Test: Venn Diagrams- 1 - Question 1

We know that x + y + z = T and x + 2y + 3z = R, where
x = number of members belonging to exactly 1 set = 70
y = number of members belonging to exactly 2 sets
z = number of members belonging to exactly 3 sets = 10
T = Total number of members
R = Repeated total of all the members = (40 + 50 + 60) = 150
Thus we have two equations and two unknowns. Solving this we get y = 25

So, 25 people belong to exactly 2 clubs.

Test: Venn Diagrams- 1 - Question 2
Save

In a class of 60, along with English as a common subject, students can opt to major in Mathematics, Physics, Biology or a combination of any two. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. In an English test, the average mark scored by students majoring in Mathematics is 45 and that of students majoring in Biology is 60. However, the combined average mark in English, of students of these two majors, is 50. What is the maximum possible number of students who major ONLY in Physics?

Detailed Solution for Test: Venn Diagrams- 1 - Question 2

​​​​​

Clear all your doubts with EduRev
Test: Venn Diagrams- 1 - Question 3
Save

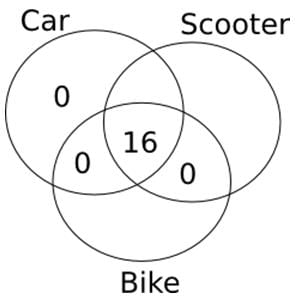
Out of 60 families living in a building, all those families which own a car own a scooter as well. No family has just a scooter and a bike. 16 families have both a car and a bike. Every family owns at least one type of vehicle and the number of families that own exactly one type of vehicle is more than the number of families that own more than one type of vehicle. What is the sum of the maximum and minimum number of families that own only a bike?

Detailed Solution for Test: Venn Diagrams- 1 - Question 3

From the information given in the question, the following Venn Diagram can be constructed:

So, in order to maximize the number of families that own only a bike, we can put the remaining 44 families in ‘only bike’ region.

Similarly, in order to minimize the number of families that own only a bike, we can put the remaining 44 families in ‘only scooter’ region.

So, the maximum number of families that own only a bike is 44 and the minimum number of families that own only a bike is 0.

So, sum = 44 + 0 = 44

Test: Venn Diagrams- 1 - Question 4
Save

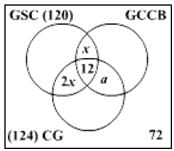
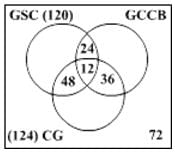
A premier B-school, which is in process of getting an AACSB accreditation, has 360 second year students. To incorporate sustainability into their curriculum, it has offered 3 new elective subjects in the second year namely Green Supply Chain, Global Climate Change & Business and Corporate Governance. Twelve students have taken all the three electives, and 120 students study Green Supply Chain. There are twice as many students who study Green Supply Chain and Corporate Governance but not Global Climate Change and Business, as those who study both Green Supply Chain and Global Climate Change & Business but not Corporate Governance, and 4 times as many who study all the three. 124 students study Corporate Governance. There are 72 students who could not muster up the courage to take up any of these subjects. The group of students who study both Green Supply Chain and Corporate Governance but not global Climate Change & Business is exactly the same as the group made up to the students who study both Global Climate Change & Business and Corporate Governance. How many students study Global Climate Change & Business only?
Detailed Solution for Test: Venn Diagrams- 1 - Question 4

The number of students who study each combination of subjects (based on the direct data) given is as shown below:

It is given that: (GSC and CG but not GCCB) = 4 times (all three electives)

∴ 2x = 4(12) i.e. x = 24

Also: (GSC and CG but not GCCB) = (all three electives) + (GCCB and CG but not GSC) 

∴ (GCCB and CG but not GSC) = 2x − 12 = 2(24) − 12 = 36

So, the figure becomes:

Now, CG only = 124 − (48 + 12 + 36) = 28 

∴ GCCB alone = 360 − 120 − 36 − 28 − 72 = 104

Hence, option (b).

Test: Venn Diagrams- 1 - Question 5
Save

In a certain village, 22% of the families own agricultural land, 18% own a mobile phone and 1600 families own both agricultural land and a mobile phone. If 68% of the families neither own agricultural land nor a mobile phone, then the total number of families living in the village is:
Detailed Solution for Test: Venn Diagrams- 1 - Question 5

Let total number of families in the village be T
Number of families own agricultural land, n(A) = 0.22T

Number of families own mobile phone, n(M) = 0.18T

Number of families own both agricultural land and mobile phone, n(A ⋂ M) = 1600

Number of families own agricultural land or mobile phone, n(A ⋃ M) = T – 0.68T = 0.32T

∴ n(A ⋃ M) = n(A) + n(M) – n(A ⋂ M)

∴ n(A ⋂ M) = 0.08T

0.08T = 1600 ⇒ T = 20000

Hence, option (a).

Test: Venn Diagrams- 1 - Question 6
Save

Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
Detailed Solution for Test: Venn Diagrams- 1 - Question 6

Now 23 students choose maths as one of their subject.
This means (MPC)+ (MC) + (PC) = 23 where MPC denotes students who choose all the three subjects maths,
physics and chemistry and so on.
So MC + PM =5 Similarly we have PC+ MP = 7
We have to find the smallest number of students choosing chemistry
For that in the first equation let PM = 5 and MC = 0. In the second equation this PC = 2
Hence minimum number of students choosing chemistry will be (18 + 2) = 20 Since 18 students chose all the
three subjects.

Test: Venn Diagrams- 1 - Question 7
Save

Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
Detailed Solution for Test: Venn Diagrams- 1 - Question 7

Let the number of students who studying only H be h, only E be e, only H and P but not E be x, only E and P but not H be y. Given only P = 0 All three = 10; Studying only H and E but not P = 20 Given number of students studying H = Number of students studying E

= h + x + 20 + 10

= e + y + 20 + 10

h + x = e + y total number of students = 74 Therefore, h + x + 20 + 10 + e + y = 74

h + x + e + y = 44 h + x + h + x = 44 h + x = 22

Therefore, the number of students studying H = h + x + 20 + 10 = 22 + 20 + 10 = 52.

Test: Venn Diagrams- 1 - Question 8
Save

A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
Detailed Solution for Test: Venn Diagrams- 1 - Question 8

Assume the number of members who can play exactly 1 game = I

The number of members who can play exactly 1 game = II

The number of members who can play exactly 1 game = III

I + 2lI + 3lll = 144 + 123 +132 = 399 .... (1)

I + lI + lII = 256 .....(2)

⇒ II + 2llI = 143. .....(3)

Also, II + 3III = 58 + 25 + 63 = 146 ......(4)

⇒ III = 3 (From 3 and 4)

⇒ II =137

⇒ I = 116

The members who play only tennis = 123 - 58 - 25 + 3 = 43

Test: Venn Diagrams- 1 - Question 9
Save

In a survey of 500 students of a college, it was found that 49% liked watching football, 53% liked watching hockey and 62% liked watching basketball. Also, 27% liked watching football and hockey both, 29% liked watching basketball and hockey both and 28% liked watching football and basketball both. 5% liked watching none of these games.

How many students like watching all the three games?
Detailed Solution for Test: Venn Diagrams- 1 - Question 9

n(F) = percentage of students who like watching football = 49%

Then n(H) = percentage of students who like watching hockey = 53%

n(B)= percentage of students who like watching basketball = 62%

n ( F ∩ H) = 27% ; n (B ∩ H) = 29% ; n(F ∩ B) = 28%

Since 5% like watching none of the given games so, n (F ∪ H ∪ B) = 95%.

Now applying the basic formula,

95% = 49% + 53% + 62% -27% – 29% – 28% + n (F ∩ H ∩ B)

Solving, you get n (F ∩ H ∩ B) = 15%. Now, make the Venn diagram as per the information given.

Note: All values in the Venn diagram are in percentage.

The number of students who like watching all the three games = 15 % of 500 = 75.

Test: Venn Diagrams- 1 - Question 10
Save

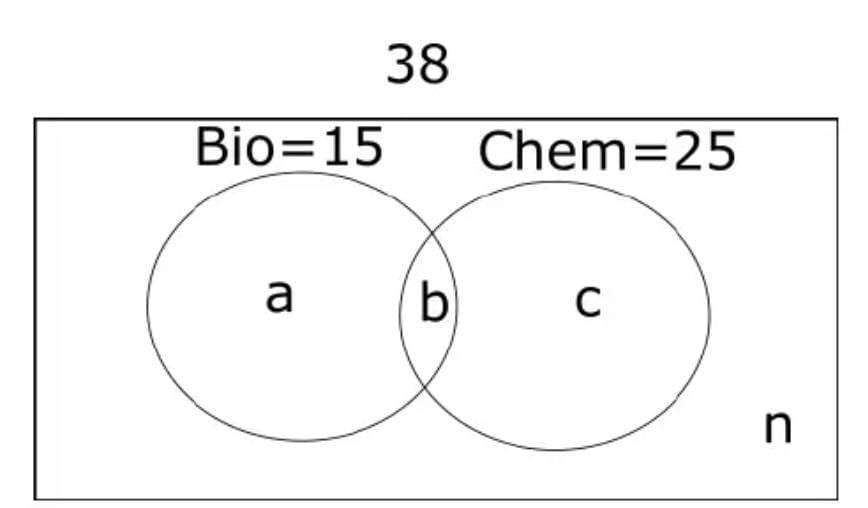
In an exam conducted for 38 students of class XII 15 passed in Biology and 25 passed in Chemistry. If atleast 1 student failed in both the subjects, find the maximum number of students who passed in only Biology?
Detailed Solution for Test: Venn Diagrams- 1 - Question 10

From the Venn diagram, a + b = 15 - (1)

b + c = 25 - (2)

a + b + c + n = 38 - (3)

(3) - (2) - (1) = b - n = 2

as n ≥ 1 the minimum value of b is 3.

From (1) the maximum value of a is 12.

Information about Test: Venn Diagrams- 1 Page
In this test you can find the Exam questions for Test: Venn Diagrams- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Venn Diagrams- 1, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for Venn Diagrams- 1

Find all the important questions for Venn Diagrams- 1 at EduRev.Get fully prepared for Venn Diagrams- 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Venn Diagrams- 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Venn Diagrams- 1 resources.

Venn Diagrams- 1 MCQs with Answers

Prepare for the Venn Diagrams- 1 within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Venn Diagrams- 1

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Venn Diagrams- 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily