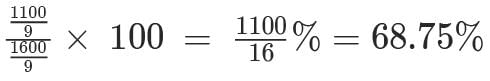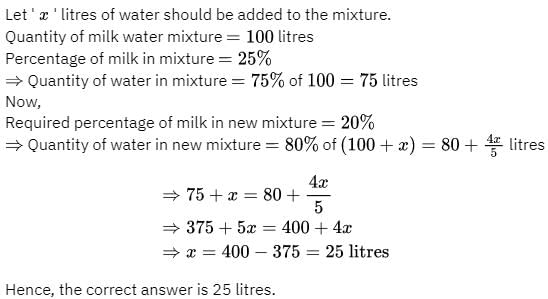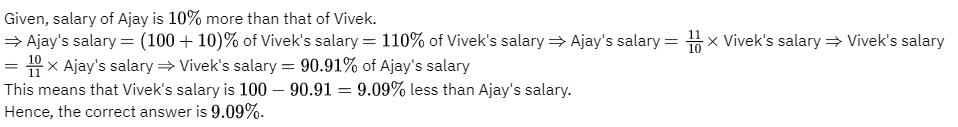Test: Arun Sharma Based Level 1: Percentages - CAT MCQ
15 Questions MCQ Test - Test: Arun Sharma Based Level 1: Percentages
What fraction is equal to 57.12% (approximately)?
a% of a + b% of b = 2% of ab, then what percentage of a is b?
The height of a triangle is increased by 30%. What can be the maximum percentage increase in length of the base, so that the increase in area is restricted to a maximum of 90%?
The length of rectangle is increased by 30% and the breadth is decreased by 25%. What is the percentage change in the area of the rectangle due to this?
At an election, the candidate who got 60% of the votes cast won by 200 votes. Find the total number of voters on the voting list, if 66.67% people cast their vote and there were no invalid votes.
A man spends 25% of his money on food. After spending 50% of the remaining, he is left with Rs 375. How much money was with that man initially?
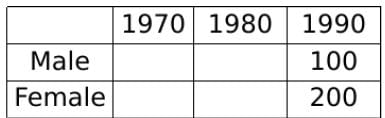
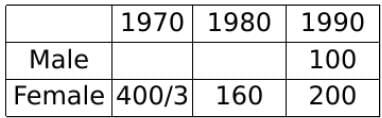
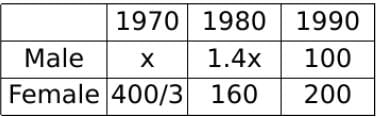
The total of male and female populations in a city increased by 25% from 1970 to 1980. During the same period, the male population increased by 40% while the female population increased by 20%. From 1980 to 1990, the female population increased by 25%. In 1990, if the female population is twice the male population, then the percentage increase in the total of male and female populations in the city from 1970 to 1990 is
In a mixture of 100 litres of milk and water, 25% of the mixture is milk. How much water should be added to the mixture, so that milk becomes 20% of the mixture?
An amount is lent at y% p.a. simple interest for two years. Instead, had it been lent at 2y% p.a. simple interest for y more years, then the interest would have been five times the earlier interest. Find the value of y.
Find the least number of integral years in which a sum of money invested at 20% compound interest per annum will become more than double itself.
Shyam invests ₹₹40000 in some shares in the ratio 1:4:5 which pay dividends of 10%, 15% and 25% (on his investment) for that year respectively. Find his dividend income.
The salary of Ajay is 10% more than that of Vivek. Find by what percentage is the salary of Vivek less than that of Ajay?
A, B and C donate 8%, 7% and 9%, of their salaries, respectively to a charitable trust. The salaries of A and B are same and the difference between their donations is 259. The total donation of A and B is 1185 more than that of C. The total donation of A and C is what percentage of the total salaries of A, B and C?
In solution of sugar and water the ratio of sugar and water by weight is 1:4. This solution is heated and in the process it loses 50% weight. What is the ratio of weight of sugar and water in the final mixture?
Dataman Infosys Systems is a Lucknow-based software company which is growing tremendously. It doubled its turnover in 1998 from Rs 50 crores in 1997. Then it tripled its turnover in 1999 and grew by 50% in 2000. What is the turnover at the end of 2000?