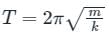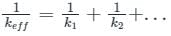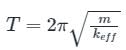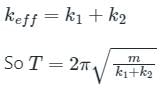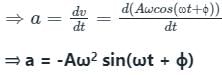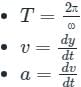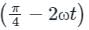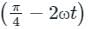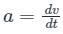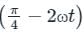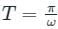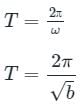Test: Oscillations - Motion of Particle in SHM (7 Oct) - JEE MCQ
10 Questions MCQ Test - Test: Oscillations - Motion of Particle in SHM (7 Oct)
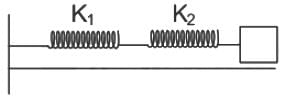
What will be time period of a spring mass system. If mass m is connected with two springs k1 and k2 in parallel.
If the distance traveled by a particle in time t is represented by x = 2 cos at - sin (2a - 1) t(a ≠ 1) and if the motion is simple harmonic motion then a = _________.
Find velocity of a particle executing shm if its displacement equation is given by x = 10 sin(2πt + ϕ).
In the simple harmonic motion, the velocity of a particle lags acceleration by ______.
The displacement of a particle is represented by the equation y = 3 cos 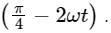 The motion of the particle is:
The motion of the particle is:
If simple harmonic motion is represented by x = A cos(ωt + φ), then 'ω' is _____________.
The acceleration of a particle performing simple harmonic motion is _____ whose displacement is f(t) = A cos(ωt + φ).
Equation of motion of a particle is given by a = -bx, where a is the acceleration, x is the displacement from the mean position and b any constant. The time period of the particle is
The body is said to move with Simple Harmonic Motion if its acceleration is ______.
If simple harmonic motion is represented by x = A cos(ωt + φ), then 'φ' is _____________.