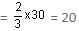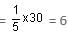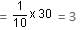All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  Test Level 2: Set Theory - 1 (October 1) - CAT MCQ

Test Level 2: Set Theory - 1 (October 1) - CAT MCQ


Test Description

10 Questions MCQ Test - Test Level 2: Set Theory - 1 (October 1)

Test Level 2: Set Theory - 1 (October 1) for CAT 2024 is part of CAT preparation. The Test Level 2: Set Theory - 1 (October 1) questions and answers have been prepared according to the CAT exam syllabus.The Test Level 2: Set Theory - 1 (October 1) MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test Level 2: Set Theory - 1 (October 1) below.
Solutions of Test Level 2: Set Theory - 1 (October 1) questions in English are available as part of our course for CAT & Test Level 2: Set Theory - 1 (October 1) solutions in Hindi for CAT course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test Level 2: Set Theory - 1 (October 1) | 10 questions in 20 minutes | Mock test for CAT preparation | Free important questions MCQ to study for CAT Exam | Download free PDF with solutions
Test Level 2: Set Theory - 1 (October 1) - Question 1
Save

A = {x : x is a perfect square; x ≤ 20; x ∈ N}
B = {y : y is not a perfect square; y ≤ 20; y ∈ N}
C = A ∪ B and D = A ∩ B

Which of the following statements is/are true?
(i) (C ∪ D) ∪ D = A ∪ B
(ii) C ∩ D = Ø
(iii) C ∪ D = C

Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 1

A = {1, 4, 9, 16}
B = {2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20}
C = A ∪ B and D = A ∩ B = {1, 2, 3, … 19, 20}
D = Ø
(i) (C ∪ D) ∪ D = A ∪ B
C ∪ D = C
C = C
(ii) C ∩ D = Ø
Ø = Ø
(ii) C ∪ D = C
C = C
All the statements are true.

Test Level 2: Set Theory - 1 (October 1) - Question 2
Save

In a locality, two-thirds of the people have Cable TV, one-fifth have VCR and one-tenth have both. What is the fraction of people having either Cable TV or VCR?

Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 2

Let us consider that the number of people in the locality be 30.
Number of persons having Cable TV 
Number of persons having VCR 
Number of persons having both 
Number of persons having either Cable TV or VCR = 20 + 6 – 3 = 23 
Required fraction  = 23/30

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test Level 2: Set Theory - 1 (October 1) - Question 3
Save

In a survey of 100 persons, it was found that 39 subscribed to TV Guide, 26 subscribed to Time and 6 subscribed to Scientific American. A total of 15 subscribed to at least two of these magazines and 2 subscribed to all the three. How many persons did not subscribe to any of the three?  

Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 3

A total of 15 persons subscribed to at least two of these magazines and 2 persons subscribed to all the three.
Then, 13 subscribed to exact two of these magazines.
Now, n(A) + n(B) + n(C) - [n(A ∩ B) + n(B ∩ C) + n(C ∩ A)] + n(A ∩ B ∩ C) = 39 + 26 + 6 - (13 + 2 + 2 + 2) + 2 = 54
Thus, out of 100 people surveyed, 54 subscribed to at least one of the three magazines or 46 did not subscribe to any of the three.

Test Level 2: Set Theory - 1 (October 1) - Question 4
Save

Directions: Study the following information and answer the question.

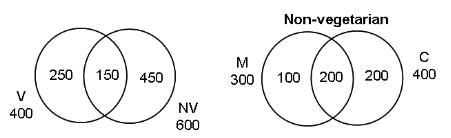
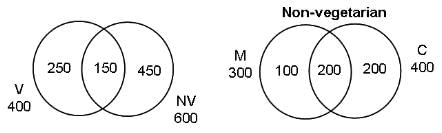
In Foodpur, where a person has to eat either vegetarian food or non-vegetarian food, there are 600 people who eat non-vegetarian food, 400 people who eat vegetarian food and 150 people who eat both. Of the people who eat non-vegetarian, there are 300 who eat mutton, 400 who eat chicken and 200 who eat both these types of meat.

Q. How many people eat vegetarian food as well as mutton?
Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 4


From the given data, number of people eating vegetarian food as well as mutton cannot be determined.

Test Level 2: Set Theory - 1 (October 1) - Question 5
Save

Directions: Study the following information and answer the question.

In Foodpur, where a person has to eat either vegetarian food or non-vegetarian food, there are 600 people who eat non-vegetarian food, 400 people who eat vegetarian food and 150 people who eat both. Of the people who eat non-vegetarian, there are 300 who eat mutton, 400 who eat chicken and 200 who eat both these types of meat.

Q. How many people do not eat chicken or mutton?
Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 5


Number of people who eat only vegetarian food = 250
Number of people who eat non-vegetarian food = 600
Number of people who eat mutton or chicken = 100 + 200 + 200 = 500
Remaining number of non-vegetarian people who do not eat mutton or chicken = 600 - 500 = 100
So, number of people who do not eat chicken or mutton = 250 + 100 = 350
 

Test Level 2: Set Theory - 1 (October 1) - Question 6
Save

At a meeting of 100 people, there were 23 Indian men and 29 Indian women. Of these Indians, 4 were dentists and 24 were either men or dentists. Assume that there were no foreign dentists. How many women dentists attended the meeting?  
Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 6

It is given that 24 were either men or dentists. We know that 23 were men, so the remaining 1 must be a woman dentist.

Test Level 2: Set Theory - 1 (October 1) - Question 7
Save

If X = {4n - 3n - 1 : n ∈ N} and Y = {9(n - 1) : n ∈ N}, then X ∪ Y is equal to
Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 7

Putting the values of n = 1, 2, 3, 4, …, we get:
X = 0, 9, 54, …
Y = 0, 9, 18, 27, 36, 45, 54, ...
Hence, X U Y will be a set equal to the value of Y.
Hence, X U Y = Y

Test Level 2: Set Theory - 1 (October 1) - Question 8
Save

In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. Each one likes at least one sport out of cricket and tennis.

How many people like tennis?
Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 8

C = Cricket
T = Tennis

Total number of people = 65
Let x be the number of people who like only tennis.
Number of people who like cricket = 40
Number of people both cricket and tennis = 10
From the Venn diagram,
40 - 10 + 10 + x = 65
x = 25
i.e. Number of people who like only tennis = 25
Number of people who like tennis = 25 + 10 = 35

Test Level 2: Set Theory - 1 (October 1) - Question 9
Save

Which of the following is an empty set?
Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 9

(A × B) ∩ (B × A) will be an empty set if A and B are disjoint. This is because in (A × B) ∩ (B × A), when we use any element, it means we are finding the common elements. But A and B are disjoint sets, so we will get zero common elements. Hence, the intersection of (A × B) and (B × A) will be a null set.

Test Level 2: Set Theory - 1 (October 1) - Question 10
Save

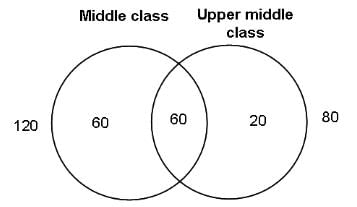
At a dinner where 240 men are seated, half of the men belong to the middle class, one third to the upper-middle class and one-fourth to both the classes. How many men belong to neither class?  
Detailed Solution for Test Level 2: Set Theory - 1 (October 1) - Question 10

This problem can be solved with the help of a Venn diagram.

Number of men belonging to the middle class = 240 × (1/2) = 120
Number of men belonging to the upper class = 240 × (1/3) = 80
Number of men belonging to both the classes = 240 × (1/4) = 60
We have identified 60 + 60 + 20 = 140 men as having well-defined class.
∴ 240 – 140 = 100 men do not belong to either class.

Information about Test Level 2: Set Theory - 1 (October 1) Page
In this test you can find the Exam questions for Test Level 2: Set Theory - 1 (October 1) solved & explained in the simplest way possible. Besides giving Questions and answers for Test Level 2: Set Theory - 1 (October 1), EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

Download as PDF

Top Courses for CAT

Important Questions for Test Level 2: Set Theory - 1 (October 1)

Find all the important questions for Test Level 2: Set Theory - 1 (October 1) at EduRev.Get fully prepared for Test Level 2: Set Theory - 1 (October 1) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Test Level 2: Set Theory - 1 (October 1) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Test Level 2: Set Theory - 1 (October 1) resources.

Test Level 2: Set Theory - 1 (October 1) MCQs with Answers

Prepare for the Test Level 2: Set Theory - 1 (October 1) within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Test Level 2: Set Theory - 1 (October 1)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Test Level 2: Set Theory - 1 (October 1) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup