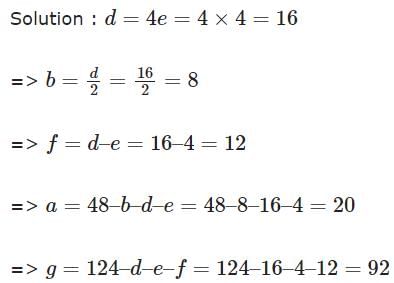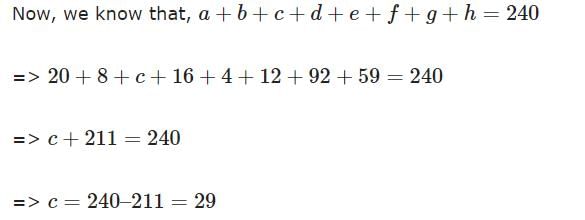Test: Set Theory- 1 - CAT MCQ
10 Questions MCQ Test - Test: Set Theory- 1
If A = {62n - 35n-1}, where n = 1,2,3, ... and B = {35(n-1)}, where n = 1,2,3, ... then which of the following is true?
For two sets A and B, let AΔB denote the set of elements which belong to A or B but not both. If P = {1,2,3,4}, Q = {2,3,5,6}, R = {1,3,7,8,9}, S = {2,4,9,10}, then the number of elements in (PΔQ)Δ(RΔS) is
If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
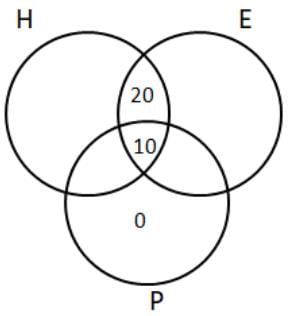
Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
In the final semester, an engineering college offers three elective courses and one mandatory course. A student has to register for exactly three courses: two electives and the mandatory course. The registration in three of the four courses is: 45, 55 and 70. What will be the number of students in the elective with the lowest registration?
70% of the students who joined XCRI last year play football, 75% play cricket, 80% play basketball and 85% play carrom. The minimum percentage of students who play all four games is:
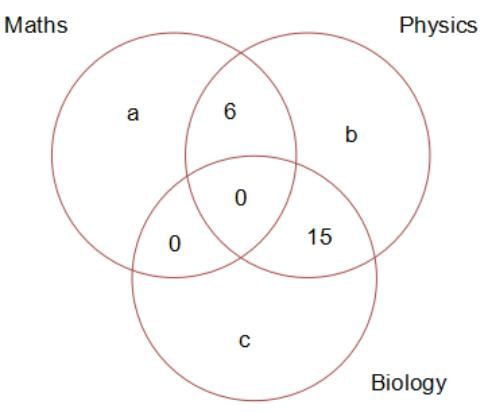
In a class of 60, along with English as a common subject, students can opt to major in Mathematics, Physics, Biology or a combination of any two. 6 students major in both Mathematics and Physics, 15 major in both Physics and Biology, but no one majors in both Mathematics and Biology. In an English test, the average mark scored by students majoring in Mathematics is 45 and that of students majoring in Biology is 60. However, the combined average mark in English, of students of these two majors, is 50. What is the maximum possible number of students who major ONLY in Physics?
In a certain village, 22% of the families own agricultural land, 18% own a mobile phone and 1600 families own both agricultural land and a mobile phone. If 68% of the families neither own agricultural land nor a mobile phone, then the total number of families living in the village is:
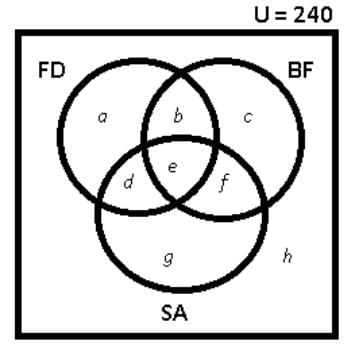
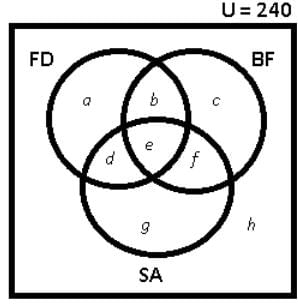
There are 240 second year students in a B – School. The Finance area offers 3 electives in the second year. These are Financial Derivatives, Behavioural Finance, and Security Analysis. Four students have taken all the three electives, and 48 students have taken Financial Derivatives. There are twice as many students who study Financial Derivatives and Security Analysis but not Behavioural Finance, as those who study both Financial Derivatives and Behavioural Finance but not Security Analysis, and 4 times as many who study all the three. 124 students study Security Analysis. There are 59 students who could not muster courage to take up any of these subjects. The group of students who study both Financial Derivatives and Security Analysis but not Behavioural Finance, is exactly the same as the group made up of students who study both Behavioural Finance and Security Analysis. How many students study Behavioural Finance only?
There are 240 second year students in a B – School. The Finance area offers 3 electives in the second year. These are Financial Derivatives, Behavioural Finance, and Security Analysis. Four students have taken all the three electives, and 48 students have taken Financial Derivatives. There are twice as many students who study Financial Derivatives and Security Analysis but not Behavioural Finance, as those who study both Financial Derivatives and Behavioural Finance but not Security Analysis, and 4 times as many who study all the three. 124 students study Security Analysis. There are 59 students who could not muster courage to take up any of these subjects. The group of students who study both Financial Derivatives and Security Analysis but not Behavioural Finance, is exactly the same as the group made up of students who study both Behavioural Finance and Security Analysis. How many students study Behavioural Finance only?



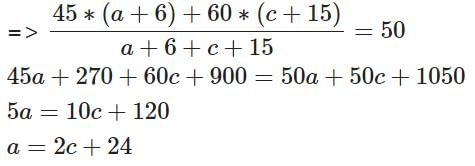
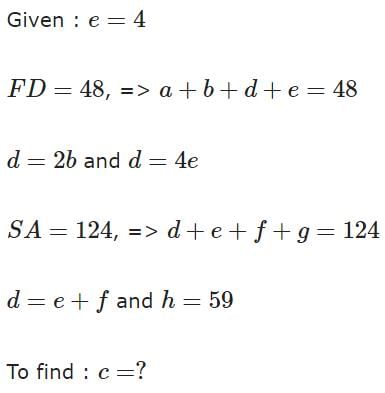
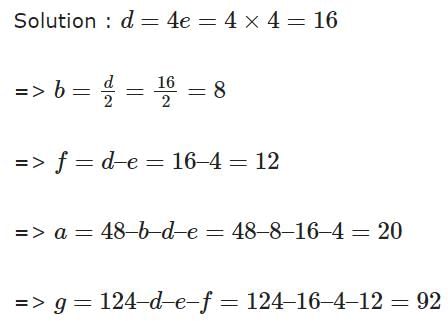
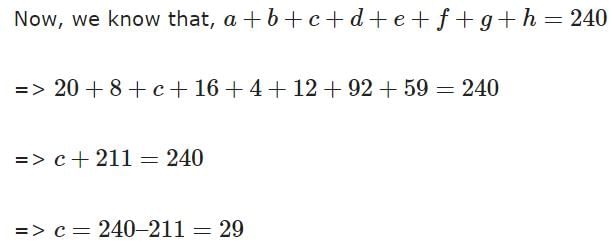
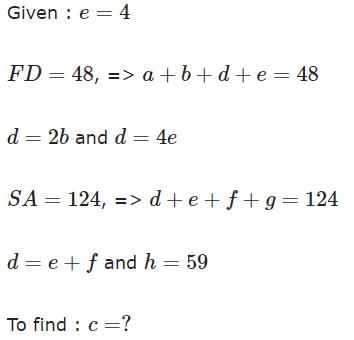 \
\