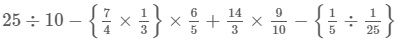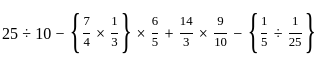RRB NTPC CBT 1 Question Paper (Held On: 4 Jan 2021 Shift 2) - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test - RRB NTPC CBT 1 Question Paper (Held On: 4 Jan 2021 Shift 2)
How many members are nominated by the President of India in the Lok Sabha from the Anglo-Indian community?
Ram Kumar bought two LED TV sets for Rs. 41,000. By selling one at a profit of 20% and the other at a loss of 15%, he found that the selling prices of both the TV sets are the same. Find his overall gain or loss.
24 mango trees, 56 apple trees and 72 orange trees have to be planted in rows such that each row contains the same number of trees of one variety only. Find the minimum number of rows in which the above mentioned trees may be planted.
Select the alphanumeric cluster from among the given options that can replace the question mark (?) in the following series.
D4C3B2A1, H8G7F6E5, L12K11J10I9, ?
The Southernmost tip of Indian territory is ______.
By selling a car for Rs. 1,20,000, David makes a profit of 20%. What will be the selling price of the car if he sells it at 30% profit?
If a + b + c = 14, ab + bc + ca = 47 and abc = 15 then find the value of a3 + b3 +c3.
Anil lent Rs. 7,200 to Dubey for 3 years and Rs. 8,400 to Raghav for 4 years on simple interest at the same rate of interest and received Rs. 4,968 in total from them as interest. Find the rate of interest p.a.
20 men and 15 boys can do a piece of work in 10 days. 25 men and 10 boys can do it in 9 days. Find the ratio of the daily work done by a man to that of a boy.
If x + x-1 = 7, then, find the value of x3 + x-3.
A few lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water such that they are fully submerged. If the diameter of the beaker is 9 cm and the water level has risen by 32 cm, find the number of lead spheres dropped into the beaker.
Select the number from among the given options that can replace the question mark (?) in the following series.
156, 182, 210, ?
Observe the figure given and answer the question below.
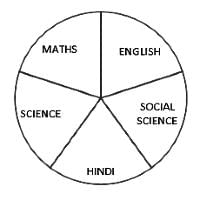
If the total number of students is 120, and the number of students is distributed equally across all the subjects, how many students study languages?
Driving his car at the speed of 30 km/h Vinod reaches his office 5 min late. If his speed is 40 km/h, he reaches the office 3 min early. Find the distance he travels between his residence and his office.
Select the option that is related to the third term in the same way as the second term is related to the first term.
Hospital : Health :: School : ?
If sec θ = 5x and tan θ = 5/x, then the value of 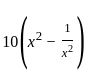 is:
is:
A question and three statements labelled (I), (II) and (III) are given. You have to decide which statement(s) is/are sufficient to answer the question.
Question: Who is the shortest among A, B, C, D and E?
Statements:
I. A is taller than E but shorter than D.
II. B is shorter than C but taller than E.
III. D is taller than C and A is taller than B.
Select the pattern from among the given options that will come next in the following series.

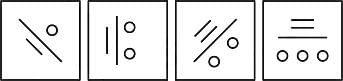
Select the option that is closest to the given shapes?
Square, Rhombus, Rectangle, Parallelogram
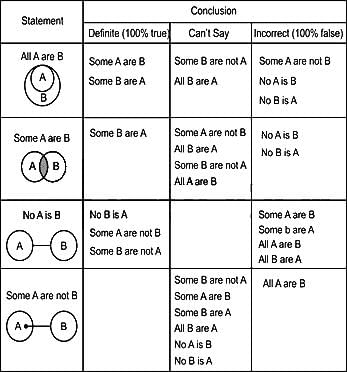
If some artists are celebrities' and ‘all celebrities are millionaires’, then which of the given conclusions follow?
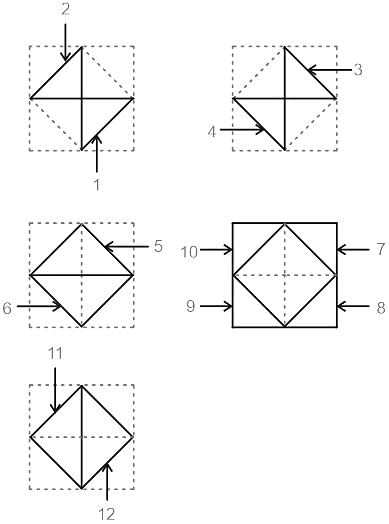
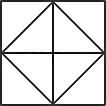
Count the number of triangles in the following figure.
Out of the four materials listed, three are alike in some manner and one is different. Select the odd one.