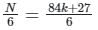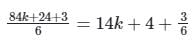Test: Number System(Tier 2) - SSC CGL MCQ
15 Questions MCQ Test - Test: Number System(Tier 2)
When a number is divided by 84, it gives 27 as the remainder. If the same number is divided by 6, then the remainder is:
The greatest number that will divide 242, 634 and 358, leaving the remainders 2, 4 and 8 respectively is:
How many numbers between 200 and 500 are completely divisible by 3, 4, and 5?
The smallest number that will be exactly divided by 625 and 250 is:
Income tax is raised from 4 paise to 5 paise in a rupee but the revenue is increased by 10% only. Find the decrease percent in the amount taxed.
Rs. 720 was divided among A, B, C, D, E. The sum received by them was in ascending order and in arithmetic progression. E received Rs. 40 more than A. How much did B receive?
Which of the following numbers is a divisor of (4915−1) ?
Four bells ring simultaneously at starting and an interval of 6 sec, 12 sec, 15 sec and 20 sec respectively. How many times they ring together in 2 hours?
If a number is in the form of 810 × 97 × 78, find the total number of prime factors of the given number.
If x2 + ax + b, when divided by x - 5, leaves a remainder of 34 and x2 + bx + a, when divided by x - 5, leaves a remainder of 52, then a + b = ?
Four bells ringing together and ring at an interval of 12 sec, 15 sec, 20 sec, and 30 sec respectively. How many times will they ring together in 8 hours?
If the 5-digit number 676xy is divisible by 3, 7 and 11, then what is the value of (3x - 5y)?
The sum of 7 consecutive natural numbers is 1617. Find how many of these are prime numbers?