Test: Elementary Mathematics - 2 - CDS MCQ
30 Questions MCQ Test - Test: Elementary Mathematics - 2
A shopkeeper offers 2 schemes of discounts. First scheme is series of discounts of 10% and 20%. Second scheme is series of discounts of 15% and 15%. Which scheme gives more discount and by how much?
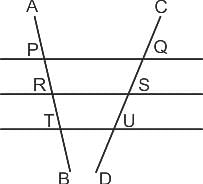
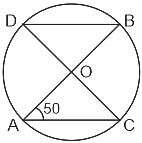
Two lines AB and CD intersects three parallel lines as shown below. If ∠APQ + ∠ARS + ∠ATU = 300° and ∠DUT + ∠DSR + ∠DQP = 210°, find the angle of intersection of the two lines AB and CD.

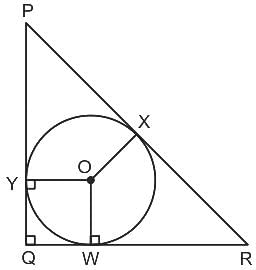
Question: What is the area of the circle?
Statement-I: The radius of the circle is one of the roots of the quadratic equation x2 - 5x + 4 = 0 for x > 0 in cm.
Statement-II: The radius of the circle is the value of cosec2 θ - cot2 θ in cm.
If N = (243 + 253 + 263 + 273), then N divided by 102 leaves a remainder of:
Which of the following statements is/are TRUE?
(A) If N = (2378)2 + 2378 + 2379, then the value of √N is 2379.
(B) The unit digit of 349 × 468 × 637 × 698 × 436 is 6.
(C) The total number of positive factors of 3024 is 40.In the following question contains STATEMENT - 1 (Assertion) and STATEMENT - 2 (Reason) and has being four choices (1), (2), (3), and (4), any one of which is the correct answer. Mark the correct choice.
Statement -1 (Assertion) : 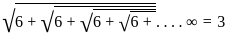
Statement - 2 (Reason) : 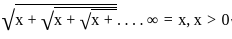
Find the value of a, if the mean of eight observation. a, a - 7, a - 4, a - 9, a - 8, a - 5, a - 12, a - 1, is 34.
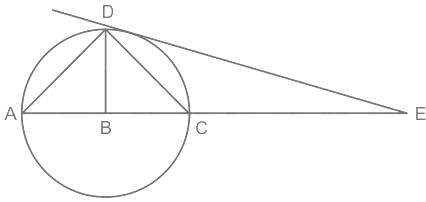
If AB ∶ AC = 1 ∶ 3 and DC = 6 cm. Then AD (in cm) is
Sports competition is organized in a college every year. 50% of total students participated in 1st year, out of which 40 students participated in 1st year only. 64% of students participated in 2nd year, out of which 50 students participated in 2nd year only. 74% of students participated in 3rd year, out of which 70 students participated in 3rd year only. How many students participated in both 2nd and 3rd years but not in 1st year. (Total number of students is 500).
Question: If the sum and product of roots of the equation x2 - bx + c = 5/2 are b and c - 5/2 respectively. Then the relation between b and c is b2 - 4c = 90.
Statement I: If the roots of the equation is differ by 5.
Statement II: If the roots of the equation is differ by 10.
Let x, y, z be fractions such that x < y < z. If z is divided by x, the result is 5/2, which exceeds y by 7/4. If x + y + z = 1(11/12), then the ratio of (z – x) : (y – x) is:
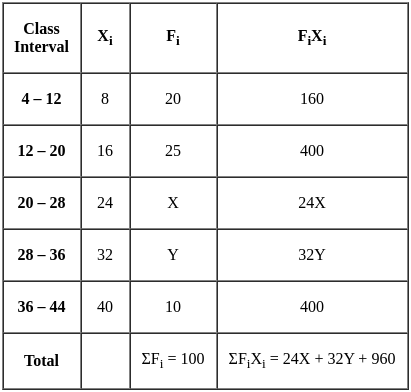
Find the value of ‘X’ if mean of frequency distribution of series I is 21.2.
If tan2A + 2tanA - 63 = 0 Given that 0 < A < (π/2) what is the value of (2sinA + 5cosA)?
what is the sum & product of roots of the given equation?
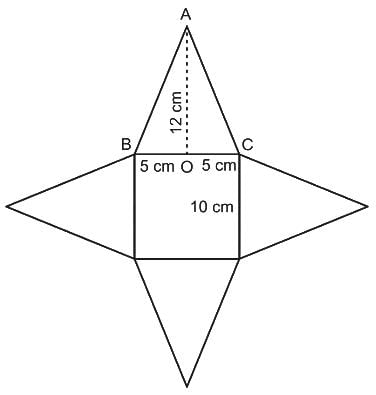
The base of a right pyramid is a square of side 10 cm. 4 rods with maximum possible length have been kept in the pyramid. The volume of the pyramid (without keeping the rods inside) is 400 cm3. The radius of the base of all the rods is 0.7 cm. What will be the approximate volume of the remaining part of the pyramid (when rods are kept inside the pyramid)?
If 43x × 47y = (2021)2, x ≠ 0, y ≠ 0, then what is the value of the following?
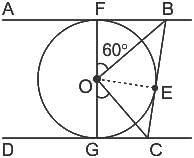
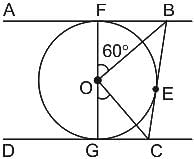
In the given figure, A tangent AB touches a circle of diameter FG at point F and tangent DC touches the circle at point G. If ∠FOB = 60∘ , then find the value of ∠GOC.
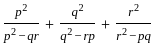 ?
?
If cos (x - y) 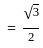 and sin (x + y) = (1/2), then the value of x (0 ≤ x ≤ 90) is:
and sin (x + y) = (1/2), then the value of x (0 ≤ x ≤ 90) is:
Which of the following statement(s) given below is / are TRUE?
A: Volume of a cylinder with base area 38.5 cm2 and curved surface area 132 cm2 is 154 cm3.
B: Total small spherical balls of radius 3 cm that can be casted after melting a large spherical ball of radius 15 cm is 25.
C: Curved surface area of a cone of base radius 7 cm and height 24 cm is 540 cm2.


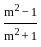 .
.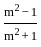
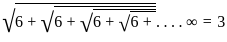
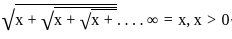
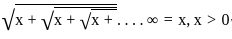
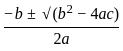
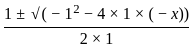
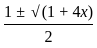 ≠ x
≠ x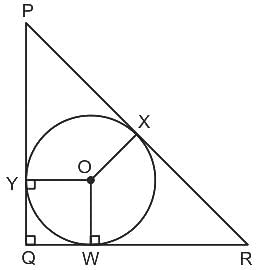
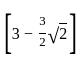 cm
cm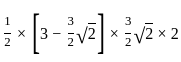
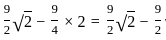
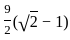 cm2
cm2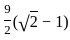 cm2.
cm2.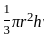
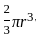
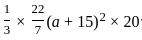 = 9240
= 9240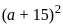 = 441
= 441 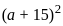 = 21
= 21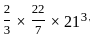
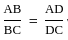
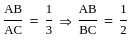
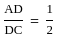
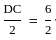 = 3 cm
= 3 cm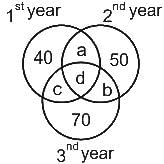

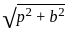
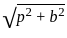
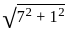 = √50
= √50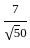 ] + [5 ×
] + [5 × 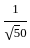 ]
]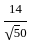 +
+ 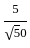 =
= 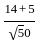 =
= 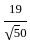
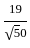
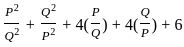 ?
?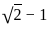 and Q =
and Q = 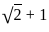
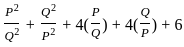
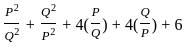
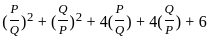
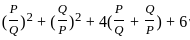
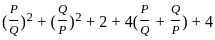
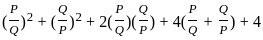
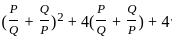
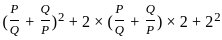
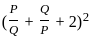 ---------- (1)
---------- (1)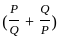
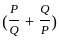 =
= 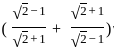
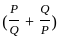 =
= 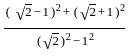
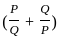 =
= 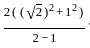
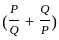 = 6
= 6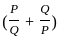 in equation (1)
in equation (1)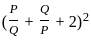 = ( 6 + 2)2
= ( 6 + 2)2 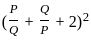 = 82
= 82 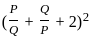 = 64
= 64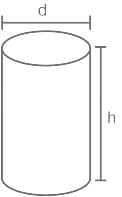
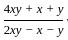
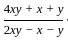
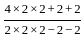 =
=