Test: Cache Memory- 1 - SSC CGL MCQ
20 Questions MCQ Test - Test: Cache Memory- 1
A file system uses an in-memory cache to cache disk blocks. The miss rate of the cache is shown in the figure. The latency to read a block from the cache is 1 ms and to read a block from the disk is 10 ms. Assume that the cost of checking whether a block exists in the cache is negligible. Available cache sizes are in multiples of 10 MB.
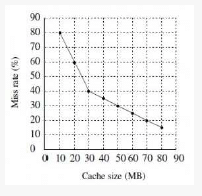
The smallest cache size required to ensure an average read latency of less than 6 ms is ______ MB.
The smallest cache size required to ensure an average read latency of less than 6 ms is ______ MB.
A block-set associative cache memory consists of 128 blocks divided into four block sets. The main memory consists of 16,384 blocks and each block contains 256 eight bit words.
- How many bits are required for addressing the main memory?
- How many bits are needed to represent the TAG, SET and WORD fields?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The access times of the main memory and the Cache memory, in a computer system, are 500 n sec and 50 n sec, respectively. It is estimated that 80% of the main memory request are for read the rest for write. The hit ratio for the read access only is 0.9 and a write-through policy (where both main and cache memories are updated simultaneously) is used.
Determine the average time of the main memory.
Determine the average time of the main memory.
A computer system has a 4 K word cache organized in block-set-associative manner with 4 blocks per set, 64 words perblock. The number of bits in the SET and WORD fields of the main memory address format is:
A computer system has a three level memory hierarchy, with access time and hit ratios as shown below:
A. What should be the minimum sizes of level 1 and 2 memories to achieve an average access time of less than 100 nsec
B. What is the average access time achieved using the chosen sizes of level 1 and level 2 memories?
On substituting the a,b for the first case we get
For a set-associative Cache organization, the parameters are as follows:
Calculate the hit ratio for a loop executed 100 times where the size of the loop is n x b and n = k x m is a non-zero integer and 1 < m ≤ l.
Give the value of the hit ratio for l = 1
The main memory of a computer has 2 cm blocks while the cache has 2c blocks. If the cache uses the set associativemapping scheme with 2 blocks per set, then block k of the main memory maps to the set
A CPU has 32-bit memory address and a 256 KB cache memory. The cache is organized as a 4-way set associative cache with cache block size of 16 bytes.
a. What is the number of sets in the cache?
b. What is the size (in bits) of the tag field per cache block?
c. What is the number and size of comparators required for tag matching?
d. How many address bits are required to find the byte offset within a cache block?
e. What is the total amount of extra memory (in bytes) required for the tag bits?
In a C program, an array is declared as float A[2048]. Each array element is 4 Bytes in size, and the starting address of the array is 0x00000000. This program is run on a computer that has a direct mapped data cache of size 8 Kbytes, with block (line) size of 16 Bytes.
a. Which elements of the array conflict with element A[0] in the data cache? Justify your answer briefly.
b. If the program accesses the elements of this array one by one in reverse order i.e., starting with the last element and ending with the first element, how many data cache misses would occur? Justify your answer briefly. Assume that the data cache is initially empty and that no other data or instruction accesses are to be considered.
Consider a small two-way set-associative cache memory, consisting of four blocks. For choosing the block to be replaced,use the least recently used (LRU) scheme. The number of cache misses for the following sequence of block addresses is8, 12, 0, 12, 8
Consider a system with 2 level cache. Access times of Level 1 cache, Level 2 cache and main memory are 1 ns, 10 ns, and500 ns, respectively. The hit rates of Level 1 and Level 2 caches are 0.8 and 0.9, respectively. What is the average accesstime of the system ignoring the search time within the cache?
Both options in choice - :OConsider a fully associative cache with 8 cache blocks (numbered 0-7) and the following sequence of memory block requests:
4, 3, 25, 8, 19, 6, 25, 8, 16, 35, 45, 22, 8, 3, 16, 25, 7
If LRU replacement policy is used, which cache block will have memory block 7?
Consider a direct mapped cache of size 32 KB with block size 32 bytes. The CPU generates 32 bit addresses. The number ofbits needed for cache indexing and the number of tag bits are respectively,
Consider a 2-way set associative cache memory with 4 sets and total 8 cache blocks (0-7) and a main memory with 128 blocks (0-127). What memory blocks will be present in the cache after the following sequence of memory block references if LRU policy is used for cache block replacement. Assuming that initially the cache did not have any memory block from the
current job?
0 5 3 9 7 0 16 55
Consider two cache organizations. First one is 32 kb 2-way set associative with 32 byte block size, the second is of same size but direct mapped. The size of an address is 32 bits in both cases . A 2-to-1 multiplexer has latency of 0.6 ns while a k - bit comparator has latency of
k/10 ns The hit latency of the set associative organization is h1 while that of direct mapped is h2
.
The value of h1 is:
Consider two cache organizations. First one is 32 kb 2-way set associative with 32 byte block size, the second is of same size but direct mapped. The size of an address is 32 bits in both cases . A 2-to-1 multiplexer has latency of 0.6 ns while a k - bit comparator has latency of
k/10 ns The hit latency of the set associative organization is h1 while that of direct mapped is h2
.
The value of h1 is:
A CPU has a 32 KB direct mapped cache with 128 byte-block size. Suppose A is two dimensional array of size with elements that occupy 8-bytes each. Consider the following two C code segments, P1 and P2.
P1:
for (i=0; i<512; i++)
{
for (j=0; j<512; j++)
{
x +=A[i] [j];
}
}
P2:
for (i=0; i<512; i++)
{
for (j=0; j<512; j++)
{
x +=A[j] [i];
}
}
P1 and P2 are executed independently with the same initial state, namely, the array A is not in the cache and i, j, x are in registers. Let the number of cache misses experienced by P1 be M1 and that for P2 be M2.
The value of M1 is:
A CPU has a 32 KB direct mapped cache with 128 byte-block size. Suppose A is two dimensional array of size with elements that occupy 8-bytes each. Consider the following two C code segments, P1 and P2.
P1:
for (i=0; i<512; i++)
{
for (j=0; j<512; j++)
{
x +=A[i] [j];
}
}
P2:
for (i=0; i<512; i++)
{
for (j=0; j<512; j++)
{
x +=A[j] [i];
}
}
P1 and P2 are executed independently with the same initial state, namely, the array A is not in the cache and i, j, x are in
registers. Let the number of cache misses experienced by P1 be M1 and that for P2 be M2.
The value of the ratio 
Top Courses for SSC CGL
Important Questions for Cache Memory- 1
Cache Memory- 1 MCQs with Answers
Online Tests for Cache Memory- 1
|
© EduRev
|
Education Revolution
|
|
