Test: Deflection of Beam,Bending Stress in Beam - 1 - Mechanical Engineering MCQ
20 Questions MCQ Test - Test: Deflection of Beam,Bending Stress in Beam - 1
A lean elastic beam of given flexural rigidity, EI, is loaded by a single force F as shown in figure. How many boundary conditions are necessary to determine the deflected centre line of the beam?
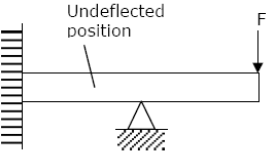
A simply supported laterally loaded beam was found to deflect more than a specified value.
Which of the following measures will reduce the deflection?
A triangular-shaped cantilever beam of uniformthickness is shown in the figure. The Young‟s modulus of the material of the beam is E. A concentrated load P is applied at the free end of the beam
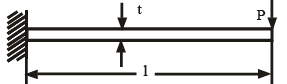
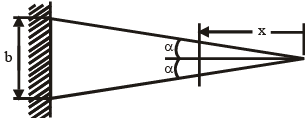
The area moment of inertia about the neutral axis of a cross-section at a distance x measure from the free end is
Consider the following statements:
In a cantilever subjected to a concentrated load at the free end
1. The bending stress is maximum at the free end
2. The maximum shear stress is constant along the length of the beam
3. The slope of the elastic curve is zero at the fixed end
The two cantilevers A and B shown in the figure have the same uniform crosssection and the same material. Free end deflection of cantilever 'A' is δ.
The value of mid- span deflection of the cantilever „B‟ is:
A simply supported beam of constant flexural rigidity and length 2L carries a concentrated load 'P' at its mid-span and the deflection under the load isδ . If a cantilever beam of the same flexural rigidity and length 'L' is subjected to load 'P' at its free end, then the deflection at the free end will be:
A cantilever beam carries a load W uniformly distributed over its entire length. If the same load is placed at the free end of the same cantilever, then the ratio of maximum deflection in the first case to that in the second case will be:
For a cantilever beam of length 'L', flexural rigidity EI and loaded at its free end by a concentrated load W, match List I with List II and select the correct answer.
List I List II
A cantilever beam of length „l‟ is subjected to a concentrated load P at a distance of l/3 from the free end. What is the deflection of the free end of the beam? (EI is the flexural rigidity)
Assertion (A): In a simply supported beam subjected to a concentrated load P at mid-span, the elastic curve slope becomes zero under the load.
Reason (R): The deflection of the beam is maximum at mid-span.
The bending moment equation, as a function of distance x measured from the left end, for a simply supported beam of span L m carrying a uniformly distributed load of intensity w N/m will be given by
A simply supported beam of rectangular section 4 cm by 6 cm carries a mid -span concentrated load such that the 6 cm side lies parallel to line of action of loading; deflection under the load is δ. If the beam is now supported with the 4 cm side parallel to line of action of loading, the deflection under the load will be:
Which one of the following is represented by the area of the S.F diagram from one end upto a given location on the beam?
In a cantilever beam, if the length is doubled while keeping the cross-section and the concentrated load acting at the free end the same, the deflection at the free end will increase by
I = 375 × 10-6 m4; l = 0.5 m E = 200 GPa
Determine the stiffness of the beam shown in the above figure
A cantilever beam has the square cross section 10mm × 10 mm. It carries a transverse load of 10 N. Considering only the bottom fibres of the beam, the correct representation of the longitudinal variation of the bending stress is:
Match the items in Columns I and II.
Beam A is simply supported at its ends and carries udl of intensity w over its entire length. It is made of steel having Young's modulus E. Beam B is cantilever and carries a udl of intensity w/4 over its entire length. It is made of brass having Young's modulus E/2. The two beams are of same length and have same cross-sectional area. If σA and σB denote the maximum bending stresses developed in beams A and B, respectively, then which one of the following is correct?
Consider the following statements in case of beams:
1. Rate of change of shear force is equal to the rate of loading at a particular section
2. Rate of change of bending moment is equal to the shear force at a particular suction.
3. Maximum shear force in a beam occurs at a point where bending moment is either zero or bending moment changes sign
Which of the above statements are correct?
Two beams of equal cross-sectional area are subjected to equal bending moment. If one beam has square cross-section and the other has circular section, then














