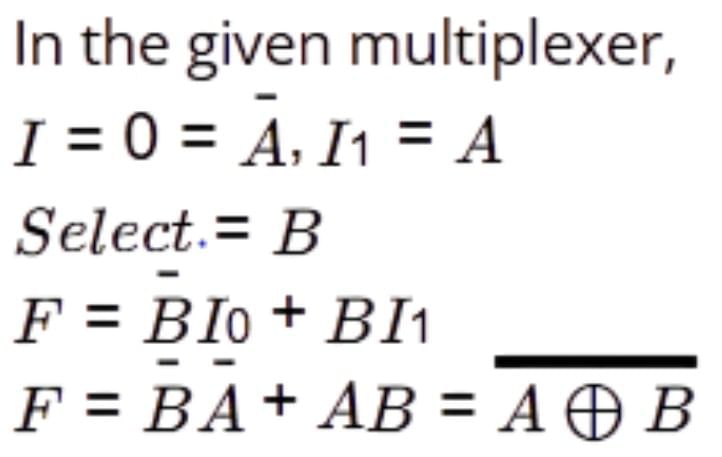Test: Number Systems, Boolean Algebra & Sequential Logic Circuits - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Number Systems, Boolean Algebra & Sequential Logic Circuits
To perform product of maxterms Boolean function must be brought into
If (211)x = (152)8 , then the value of base x is
11001, 1001 and 111001 correspond to the 2’s complement representation of the following set of numbers
A signed integer has been stored in a byte using 2’s complement format. We wish to store the same integer in 16-bit word. We should copy the original byte to the less significant byte of the word and fill the more significant byte with
A computer has the following negative numbers stored in binary form as shown. The wrongly stored number is
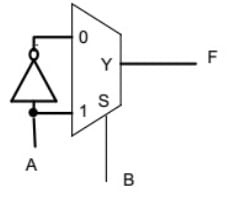
Consider the following circuit which uses a 2-to-1 multiplexer as shown in the figure below. The Boolean expression for output F in terms of A and B is
The counter shown in fig. is
The counter shown in fig. counts from
The mod-number of the asynchronous counter shown in fig. is
The frequency of the pulse at z in the network shown in fig. is
The three-stage Johnson counter as shown in fig. is clocked at a constant frequency of fc from the starting state of Q2 Q1Q0 = 101. The frequency of output Q2 Q1Q0 will be
The counter shown in the fig. has initially Q2Q1Q0 = 000. The status of Q2 Q1Q0 after the first pulse is
A 4 bit ripple counter and a 4 bit synchronous counter are made by flips flops having a propagation delay of 10 ns each. If the worst case delay in the ripple counter and the synchronous counter be R and S respectively, then
A 4 bit modulo–6 ripple counter uses JK flip-flop. If the propagation delay of each FF is 50 ns, the maximum clock frequency that can be used is equal to
The initial contents of the 4-bit serial-in-parallel-out right-shift, register shown in fig. is 0 1 1 0. After three clock pulses are applied, the contents of the shift register will be
Consider the signed binary number A = 01010110 and B = 1110 1100 where B is the 1’s complement and MSB is the sign bit. In list-I operation is given, and in list-II resultant binary number is given.
The correct match is
The simplified form of a logic function
If the decimal number is a fraction then its binary equivalent is obtained by ________ the number continuously by 2.
The Boolean equation X = [(A + B̅) (B + C)] B can be simplified to