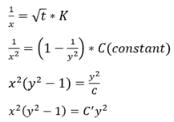JEE Advanced Level Test: Differential Equation - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Differential Equation
If sin x is an integrating factor of the differential equation 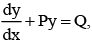 then P can be
then P can be
Solution of the differential equation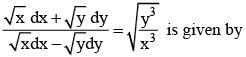
The degree of the differential equation of all curves having normal of constant length c, is
The equation of the curve in which the portion of the tangent included between the coordinate axes is bisected at the point of contact, is
Solution of the differential equation
Consider the differential equation
Then x is given by:
The equation of the curve for which the tangent at P(x, y) cuts the y-axis at (0, y3) is
then the solution of the equation is
Find the area of smaller portion of the circle x2 + y2 = 4 cut off by the line x = 1.
The region bounded by the curve = log x and y = 2x , then the area of the region, is
The order and degree of the differential equation, of which xy = cex + be-x + x2 is a solution, is
The order of the differential equation whose general solution is given by
The degree of the differential equation satisfying
The differential equation of the family of curves y = ex (A cos x + B sin x) , where A and B are arbitrary constants, is
The differential equation of family of parabolas with foci at the origin and axis along the x-axis, is
Solution of the equation
(x - y) (2dy - dx) = 3dx - 5dy is
A curve passes through the point and its slope at any point is given by
Then, the curve has the equation
A function y = f (x) satisfies the condition f ' (x) sin x + f (x) cos x= 1, f (x) being bounded when
A function y = f (x) satisfies (0) = 5, then f (x ) is
The solution of satisfying y (1) = 0 is given by
The solution of the differential equation, given
The solution of sec y satisfying y (1) = 0, is
If normal at every point to a curve passes through a fixed point then the curve must be
Solution of the differential equation
The equation of the curve which passes through the point (2a, a) and for which the sum of the Cartesian sub tangent and the abscissa is equal to the constant a, is
Water is drained from a vertical cylindrical tank by opening a valve at the base of the tank. It is known that the rate at which the water level drops is proportional to the square root of water depth y, where the constant of proportionality k > 0 depends on the acceleration due to gravity and the geometry of the hole. If t is measured in minutes and then the time to drain the tank, if the water is 4 meter deep to start with is
A ray of light coming from origin after reflection at the point P(x, y) of any curve becomes parallel to x-axis, if the curve passes through (8, 6) then its equation is
A function y = f (x) has a second order derivative f "(x) = 6 (x - 1). If its graph passes through the point (2, 1) and at that point the tangent to the graph is y = 3x- 5, then the function is