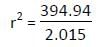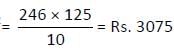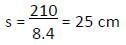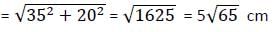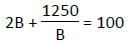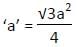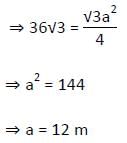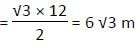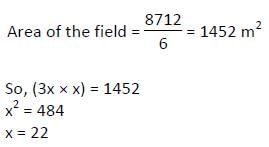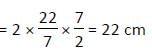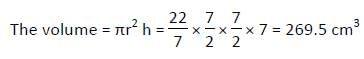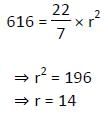MCQ: क्षेत्र - 2 - Bank Exams MCQ
15 Questions MCQ Test - MCQ: क्षेत्र - 2
यदि एक आयत की लंबाई 25% बढ़ाई जाती है और चौड़ाई 33.33% घटाई जाती है, तो इसके विकर्ण पर क्या प्रभाव पड़ेगा (लगभग)?
एक आयत की परिधि, जिसकी लंबाई 2 (x + 3) सेमी और चौड़ाई 2 (x + 1) सेमी है, एक वर्ग की परिधि से दोगुनी है, जिसका क्षेत्रफल 225 सेमी2 है। आयत का क्षेत्रफल ज्ञात करें।
गोलाकार क्षेत्रफल और आयत के क्षेत्रफल के बीच का अंतर 394.94 सेमी2 है। यदि आयत की लंबाई वृत्त के त्रिज्या से 25% अधिक है और चौड़ाई 10% कम है, तो आयत का परिमाप क्या होगा? (π = 3.14 मानकर चलें)
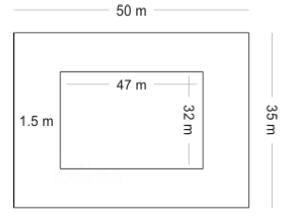
एक आयताकार पार्क के अंदर 1.5 मीटर चौड़ाई का एक ट्रैक बनाया गया है, जिसकी लंबाई 50 मीटर और चौड़ाई 35 मीटर है। ट्रैक पर ईंटें बिछाने की कुल लागत क्या होगी, यदि दर 10 मीटर2 के लिए 125 रुपये है?
एक आयत (R) और एक वर्ग (S) के परिधियों का योग 210 सेमी है। यदि आयत (R) की लंबाई वर्ग (S) के पक्ष से 40% अधिक और चौड़ाई 20% कम है, तो आयत (R) का विकर्ण (diagonal) क्या होगा?
एक जौहरी 1250 वर्ग मीटर के आयताकार आभूषण की दुकान बनाना चाहती है। चूंकि उसके पास केवल 100 मीटर कांटेदार तार है, उसने आभूषण की दुकान के तीन पक्षों को बार्ब किया, जिससे उसका घर की दीवार दुकान के शेष पक्ष के रूप में कार्य कर रही है। उस आभूषण की दुकान का आयाम क्या है जहाँ कांटेदार तार का उपयोग किया जा रहा है?
यदि एक समभुज त्रिकोण का क्षेत्रफल 36√3 मी2 है, तो उसकी ऊँचाई ज्ञात कीजिए?
एक आयताकार खेत की चौड़ाई और लंबाई का अनुपात 1 : 3 है। खेत की घास काटने की कुल लागत प्रति वर्ग मीटर 6 रुपये की दर से 8712 रुपये है। खेत की सीमा को 11 रुपये प्रति मीटर की दर से बाड़ लगाने की लागत ज्ञात करें।
एक आयत के क्षेत्रफल का अनुपात एक वर्ग के क्षेत्रफल के साथ 3 : 5 है। यदि वर्ग का परिमाप 100 सेमी है, तो यदि आयत की चौड़ाई उसकी लंबाई से 66.67% अधिक है, तो आयत का परिमाप क्या हो सकता है?
एक क्यूबॉइड के आकार 15 मीटर x 20 मीटर x 18 मीटर को अंदर और बाहर से 5 पैसे प्रति वर्ग मीटर की दर से रंगा गया। यदि क्यूबॉइड धातु का बना है जिसका मोटाई नगण्य है, तो क्यूबॉइड को अंदर और बाहर रंगने के लिए कितने पैसे (रुपयों में) की आवश्यकता होगी?
एक समांतर चतुर्भुज के आकार के खेत में, एक पक्ष की लंबाई 15 मीटर है और विपरीत पक्षों के बीच लंबवत दूरी 16 मीटर है। यदि इस खेत में गेहूं के बीजों की बुवाई की जाती है, जिसकी दर Rs. 15 प्रति वर्ग मीटर है, तो खेत में गेहूं के बीजों की बुवाई के लिए कितने पैसे की आवश्यकता होगी?
एक बेलनाकार आकृति की लकड़ी की ऊँचाई उसके आधार की परिधि से 15 सेमी कम है और उसकी वक्र सतह क्षेत्रफल 154 सेमी2 है, तो इस बेलनाकार लकड़ी का आयतन (सेमी3 में) क्या होगा?
एक बेलन और एक शंकु के आयतन का योग 2190π सेमी2 है। दोनों बेलन और शंकु की त्रिज्या समान है, अर्थात्, 10 सेमी। यदि शंकु की ऊँचाई 15 सेमी है, तो बेलन की ऊँचाई की शंकु की ऊँचाई के साथ अनुपात ज्ञात कीजिए?
एक त्रिकोणीय क्षेत्र को लोहे की तार से बाड़ा जाना है। बाड़ लगाने की लागत प्रति मीटर 15 रुपये है। यदि त्रिकोणीय क्षेत्र के तीन पक्षों में से दो के लंबाई का योग 25 मीटर है, तो निम्नलिखित में से कौन सी लागत क्षेत्र की बाड़ लगाने की नहीं हो सकती?
गोलाकार क्षेत्रफल 616 सेमी2 है, आयत की चौड़ाई वृत्त की त्रिज्या की आधी है। आयत की लंबाई आयत के परिमाप का 37.5% है। यदि एक वर्ग की भुजा आयत की लंबाई का दो गुना है, तो वर्ग का क्षेत्रफल ज्ञात करें।