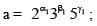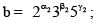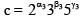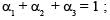JEE Advanced Level Test: Permutation And Combinations- 2 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Permutation And Combinations- 2
The total number of ways of dividing 15 different things into groups of 8, 4 and 3 respectively is
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is
Total number of four digit odd numbers that can be formed using 0, 1, 2, 3, 4, 5, 7 are
A box contains 5 different red and 6 different white balls. In how many ways can 6 balls be selected so that there are at least two balls of each colour
The number of positive integral solutions abc = 30 is
Number of ways of dividing 80 cards into 5 equal group of 16 each is
The sum of the divisors of 25. 34. 52 is
A committee of 5 is to be formed from 6 boys and 5 girls. The number of ways so that the committee can be formed so that the committee contains at least one boy and one girl having majority of boys is
The number of ways in which n distinct objects can be put into two different boxes so that no box remains empty is
Number of ways of selecting 6 shoes, out of 8 pairs of shoes, having exactly two pairs is
The number of words that can be formed from the letters of the word “INTERMEDIATE” in which no two vowels are together is
The number of more words can be found by rearranging the letters of the word „CHEESE‟ are
The number of ways in which 5 boys and 3 girls can sit around a round table so that all the girls are not sit together is
The number of three digit numbers of the form xyz where x > y > z is
Three men have 4 coats, 5 waist coats and 6 caps. The number of ways they can wear them is
The number of words that can be formed by using all the letters of the word “KANPUR” when the vowels are in even places is
If repetitions are not allowed, the number of numbers consisting of 4 digits and divisible by 5 and formed out of 0, 1, 2, 3, 4, 5, 6 is
A polygon has 35 diagonals. The number of its sides are
The number of rectangles on a chess board is
The rank of the work “MADHUR” when arranged in dictionary order is
20 persons are invited for a party. The different number of ways in which they can be seated around a circular table with two particular persons seated on the either side of the host are
The number of ways of arranging the letters of the word DEVIL so that neither D is the first letter nor L is the last letter is
In how many ways can 3 sovereigns be given when there are 4 applicants and any applicant may have either 0, 1, 2 or 3 sovereigns?
In the word „ENGINEERING‟ if all E‟s are not together and N‟s come together then number of permutations is
The number of permutation that can be made out of the letters of the word „MATHEMATICS‟. When no two vowels come together is
The number of different numbers each of six digits than can be formed by using the digits of the numbers 2, 2, 3, 3, 9, 9 is
The number of ways so that all the letters of the word „SWORD‟ can be arranged such that no letter is in its original position is
The number of two digit numbers which are of the form xy with y < x are given by
The number of proper divisors of 2160 is
Total number of words formed by 2 vowels and 3 consonants taken from 4 vowels and 5 consonants is equal to