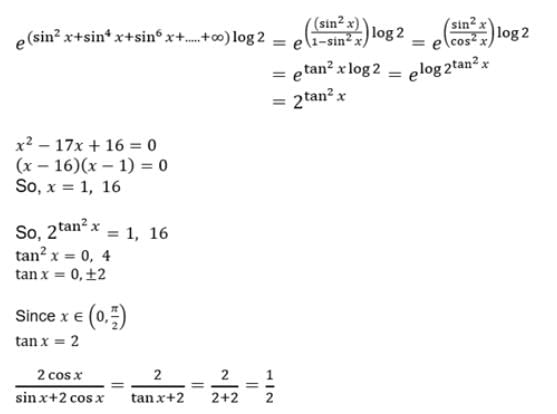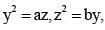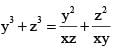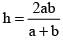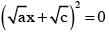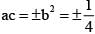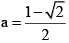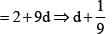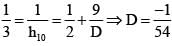JEE Advanced Level Test: Sequences And Series- 2 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Sequences And Series- 2
If ar > 0, r ∈ N and a1, a2 , a3 , .............a2n are A.P. then
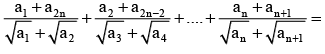
If a, b, c, d, e, f are in A.P., then e-c is equal to
If the roots of the cubic equation ax3 + bx2 + cx + d = 0 are in G.P., then
If one A.M. a and two G.M.’s p and q be inserted between any two numbers, then the value of p3 + q3 is
If –1 < a, b, c < 1 and a, b, c are in A.P. and then x, y, z are in
Number of positive integral ordered pairs of (a, b) such that 6, a, b are in H.P is
If exp {(sin2x +sin4x + sin6x + upto ∞)loge2} satisfies the equation x2 – 17x + 16 = 0 then the value of 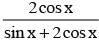 (0 < x < π/2) is
(0 < x < π/2) is
If tn denotes nth term of the series 2 + 3 + 6 + 11 + 18 + ..... then t50
If a, 8, b are in A.P., a, 4, b are in G.P; a, x, b are in H.P then x =
If a, b, c are in H.P., then the straight line always passes through a fixed point. That point is
Let x be the arithmetic mean and y, z be the two geometric means between any two positive numbers. Then value of
If a, a1, a2, a3, a4, ......, a2n, b are in AP and a, g1, g2, g3, g4,........g2n, b are in GP and h is the HM of a and b then 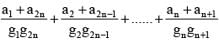 is equal to
is equal to
The arithmetic mean between 2+√(2) and 2-√(2) is
If cos (x, -y), cos x and cos (x + y) are in H.P, then value of cos x sec (y/2) is
If a, b, c are in G.P., then the equations ax2 + 2bx + c = 0 and dx2 + 2ex + f = 0 have a common root if a/d, b/e, c/f are in
If a, b, c, d, x are real and the roots of equation (a2 + b2 + c2)x2 - 2 (ab + bc + cd)x + (b2 + c2 + d2) = 0 real and equal, then a, b, c, d are in
The natural numbers are divided into groups 1, (2, 3), (4, 5, 6), (7, 8, 9, 10)....; then the sum of the numbers in the 50th group is
If a, b and c are in G.P., then the equations ax2 + 2bx + c = 0 and dx2 + 2ex + f = 0 have a common root
Suppose a, b, c are in A.P. a2, b2, c2 are in G.P. If a < b < c and a b c and a + b + c = 3/2, then the value of a is
The question should be:If the ratio of nth terms of two A.P.'s is (2n+8):(5n−3), then the ratio of the sums of their n terms is
H1, H2 are 2 H.M.’s between a, b then
The number of common terms in two A.P’s 2, 7, 12, 17............. 500 terms and 1, 8, 15, 22,..........300 terms is
If log 2, log (2x - 1) and log (2x + 3) are in AP, then the value of x is given by
If a1, a2 , a3...........an are in HP then a1a2 + a2a3 + a3a4 + ..... + an-1an =
Let a1, a2, ..... a10 be in A.P. and h1, h2, ......h10 be in H.P. If a1 = h1 = 2 and a10 = h10 = 3, then a4h7 is
The sum to 50 terms of the series
If the sum to infinity of the series 1 + 2r + 3r2 + 4r3 + ... is 9/4, then value of r is


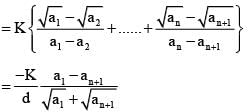

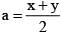

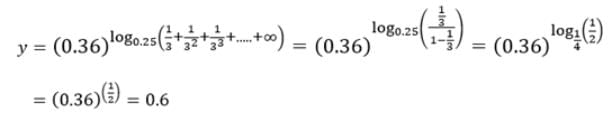
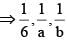 are in A.P.
are in A.P.