MCQ (Previous Year Questions) - Tangent And Normal (Competition Level 1) - JEE MCQ

If the equation anxn + a_n–1 x^n–1 +....+ a₁x= 0 ; a₁ ≠ 0, n ≥ 2, has a positive root x =α, then the equation na_nx^n–1 + (n – 1) a_n–1 x^n–2 + .... + a₁ = 0 has a positive root, which is -

[AIEEE-2005]

The normal to the curve x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ) at any point 'θ' is such that -

A spherical iron ball 10 cm in radius is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm³/min. When the thickness of ice is 5 cm, then the rate of which the thickness of ice decreases, is -

[AIEEE-2005]

Angle between the tangents to the curve y=x² – 5x+6 at the points (2, 0) and (3, 0) is–

[AIEEE 2006]

The equation of the tangent to the curve y = x + 4/x² , that is parallel to the x–axis, is -  

[AIEEE 2010]

The shortest distance between line y – x = 1 and curve x = y² is:

[AIEEE 2011]

The intercepts on x-axis made by tangents to the curve, 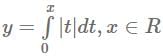  which are parallel to the line y =2x, are equal to :

 [JEE MAIN 2013]

Find the equation of the straight line which is tangent at one point and normal at another point of the curve,
x = 3t², y = 2t³.

[REE 2000 (Mains), 5]

If the normal to the curve, y = f(x) at the point (3, 4) makes an angle 3π/4 with the positive x-axis. The f ’(3)=

[JEE 2000 (Scr.), 1]

The point(s) on the curve y³ + 3x² = 12y where the tangent is vertical, is (are)

 [JEE 2002 (Scr.), 3]

The tangent to the curve y = e^x drawn at the point (c, e^c) intersects the line joining the points (c – 1, e^c1) and (c + 1, e^{c + 1})

[JEE 2007, 3]

Tangent to the curve y = x² + 6 at a point P(1, 7) touches the circle x² + y² + 16x + 12y + c = 0 at a point Q. Then the coordinates of Q are    

[JEE 2005 (Scr.), 3]