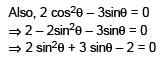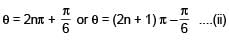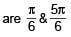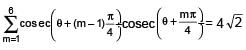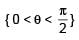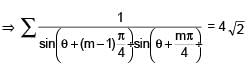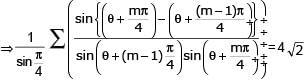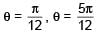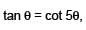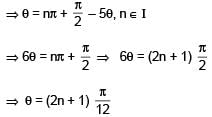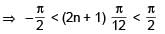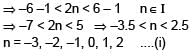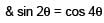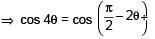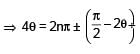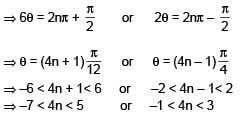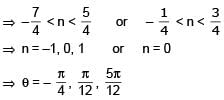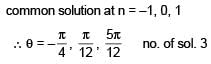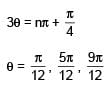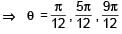MCQ (Previous Year Questions) - Trigonometry Equation (Competition Level 1) - JEE MCQ
12 Questions MCQ Test - MCQ (Previous Year Questions) - Trigonometry Equation (Competition Level 1)
Find the no. of roots of the equation tan x + sec x = 2 cos x in the interval [0, 2 π]-
General solution of tan 5θ = cot 2θ is-
The number of values of x in the interval [0, 3π]satisfying the equation 2 sin2 x + 5 sin x – 3 = 0 is –
If 0 < x < π, and cos x + sin x =1/2 , then tan x is –
The number of integral values of k for which the equation 7 cos x + 5 sin x = 2k + 1 has a solution is
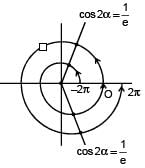
cos(α – β) = 1 and cos(α + β) = 1/e, where α,β ∈ [–π, π], number of pairs of a, b which satisfy both the equations is
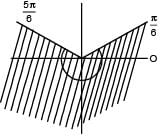
If 0 < θ < 2π, then the intervals of values of θ for which 2 sin2θ – 5sinθ + 2 > 0, is
The number of solutions of the pair of equations 2sin2θ – cos 2θ = 0 and 2cos2θ– 3 sin θ = 0 in the interval [0, 2π] is
For 0 < θ < π/2, then solution(s) of 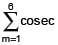 (θ + (m - 1)π/4) cosec(θ + mπ/4) = 4,√2 is(are)
(θ + (m - 1)π/4) cosec(θ + mπ/4) = 4,√2 is(are)
The number of values of θ in the interval 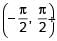 such that
such that 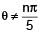 for n= 0, ±1, ±2 and tanθ = cot 5θ as well as sin2θ = cos4θ is
for n= 0, ±1, ±2 and tanθ = cot 5θ as well as sin2θ = cos4θ is
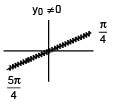
The number of all possible values of θ when θ ∈(0, π) for which the system of equation (y + z) cos 3θ = (xyz) sin 3θ(xyz) sin 3θ = (y + 2z)cos 3θ + y sin 3θ have a solution (x0, y0, z0) with y0,z0 ≠ 0 is
Let P = {θ : sin θ – cos θ = √2 cos θ} and Q = {θ : sin θ + cos θ = 2 sin θ} be two sets. Then


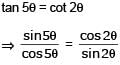
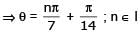

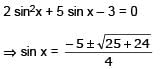
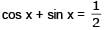

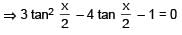
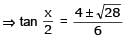

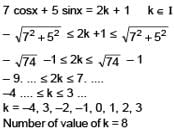
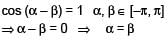
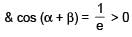
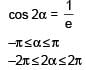
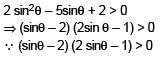
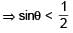
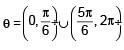
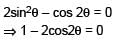
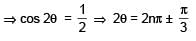
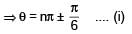 n ∈ I
n ∈ I