SRMJEE Mock Test - 9 (Engineering) - JEE MCQ
30 Questions MCQ Test - SRMJEE Mock Test - 9 (Engineering)
A resistance of 8 ohms is connected in series with another resistance of 4 ohms. A potential difference of 24 volts is applied across the combination. Calculate the current through the circuit.
In an electromagnetic wave in free space, the root mean square value of the electric field is Erms = 6 V/m. The peak value of the magnetic field is
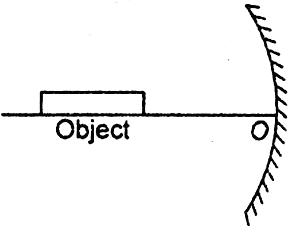
A short linear object of length 'b' lies along the axis of a concave mirror of focal length 'f' at a distance 'u' from the pole of the mirror. What is the size of the image of the object?
A particle starts from rest with uniform acceleration a. Its velocity after n seconds is v. The displacement of the particle in the last two seconds is:
At critical temperature, the surface tension of a liquid is
The time period of a satellite of earth is 5 hr. If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become
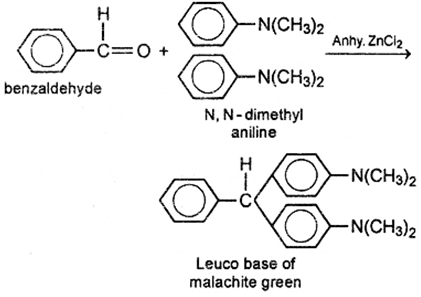
Benzaldehyde condenses with N,N-dimethylaniline in presence of anhydrous ZnCl2 to give
Directions: In the following question, two statements are given. One is assertion and the other is reason. Examine the statements carefully and mark the correct answer according to the instructions given below.
Assertion: Deoxyribose (C5H10O4) is not a carbohydrate.
Reason: Carbohydrates are hydrates of carbon. So, the compounds which follow Cx(H2O)y formula are carbohydrates.
For electroplating, 1.5 amp current is passed for 250 s through 250 mL of 0.15 M solution of MSO4. Only 85% of the current was utilised for electrolysis. The molarity of MSO4 solution, after electrolysis, is closest to
[Assume that volume of the solution remained constant]
A synthetic rubber which is resistant to the action of oils, gasoline and other solvents, is-
The change in the optical rotation of a freshly prepared solution of glucose is known as
The oxidation of benzyl chloride with lead nitrate gives
If m is chosen in the quadratic equation (m2 + 1) x2 - 3x + (m2 + 1)2 = 0, such that, the sum of its roots is greatest, then the absolute difference of the cubes of its roots is:
The system of equations
λx + y + z = 0,
– x + λy + z = 0,
– x – y + λz = 0
will have a non-trivial solution if real values of λ are
The complete set of values of x for which 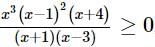 , is
, is
The number of ordered triplets (x, y, z) that satisfy the equation 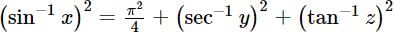 :
:
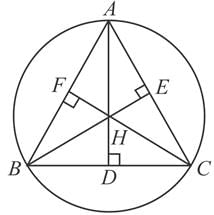
The vertices of a variable acute-angled triangle ABC lie on a fixed circle. Also, a, b, c are the lengths of the sides, and A, B, C are the angles of the triangle ABC, respectively.If x₁, x₂, and x₃ are the distances of the orthocentre from A, B, and C, respectively, then the maximum value of (d(x₁)/da + d(x₂)/db + d(x₃)/dc) is:
If the sum and product of the first three terms in an A.P. are 33 and 1155, respectively, then a value of its 11th term is:
If the line |y| = x - α, α > 0 does not meet the circle x² + y² - 10x + 21 = 0, then α ∈:
If g(x) = 2f(2x³ − 3x²) + f(6x² − 4x³ − 3), ∀x ∈ R and f″(x) > 0, ∀x ∈ R, then g(x) is increasing for x belonging to:
The common tangent to the circles x² + y² = 4 and x² + y² + 6x + 8y − 24 = 0 also passes through the point:
If f is an even function and g is an odd function, then the function fog is
In the following figure, ABCD is a square with an area of 64 cm2. Find the area of ΔDCE.








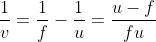
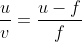
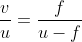 ...(iii)
...(iii)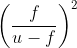 b
b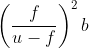 .
. 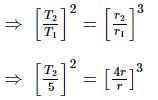


 order: HCIO4 < HClO3 < HCIO2 < HCIO
order: HCIO4 < HClO3 < HCIO2 < HCIO 
 = 0.0375 (initial mole)
= 0.0375 (initial mole) = 0.143
= 0.143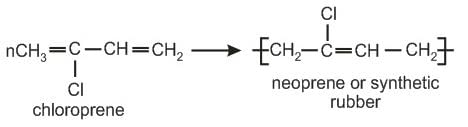
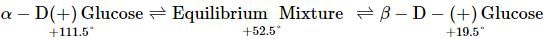
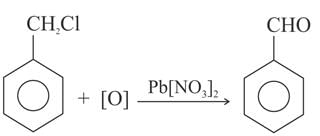
 )
) )
) ) - (
) - ( + 35X + 25)
+ 35X + 25) + 15X - 25
+ 15X - 25 =
=  + 15 = 0
+ 15 = 0 = -
= -  < 0 (at X = 10),
< 0 (at X = 10),

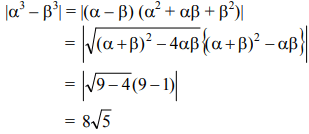
 = tan-1 x + cot -1 x =
= tan-1 x + cot -1 x = 
 .
.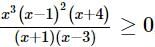


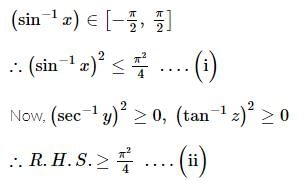
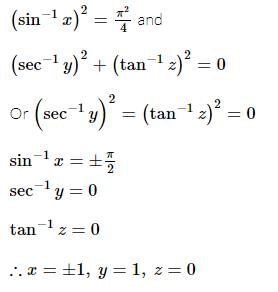
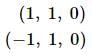
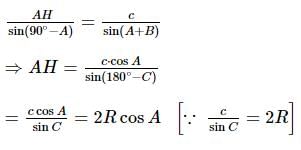
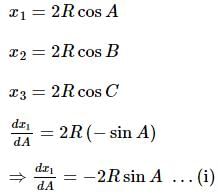
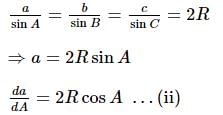
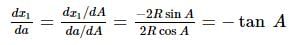
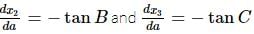
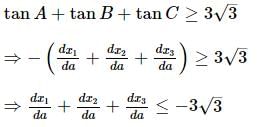
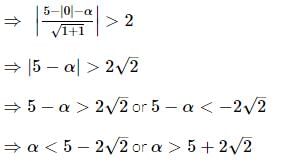

 DCE = 4 × 8 = 32 sq. cm
DCE = 4 × 8 = 32 sq. cm
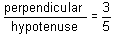
 = 4k
= 4k
















