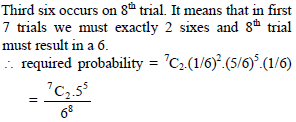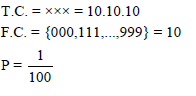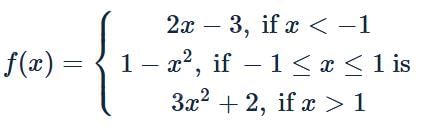Mathematics: CUET Mock Test - 1 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 1
If the probability of solving a problem by three students are 1/2,1/3 and 1/4 then probability that the problem will be solved-
Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is-
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is
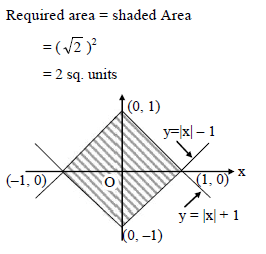
The area bounded by the curve y = | x | – 1 and y = – | x | + 1 is -
Maximize Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Find the maximum value of z = 3x + 4y subject to constraints x + y ≤ 4 , x ≥ 0 and y ≥ 0
The number of all possible matrices of order 3×3 with each entry 0 or 1 is
In a binomial distribution, if the probability of at least one success is greater than or equal to 9/10, then n is greater than :
A random variable X has the probability distribution: P(X = x) = kx² for x = 1, 2, 3. What is the expected value of X?
A random variable X has a binomial distribution with n = 15 and p = 0.2. What is the probability that X is greater than or equal to 5?
A fair dice is tossed eight times. Probability that on the eighth throw a third six is observed is -
The last three digits of a telephone number beginning with 135 _ _ _ have been erased. The probability that the erased digits will be all identical is -
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines tomanufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
Determine the maximum value of Z = 11x + 7y subject to the constraints :2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
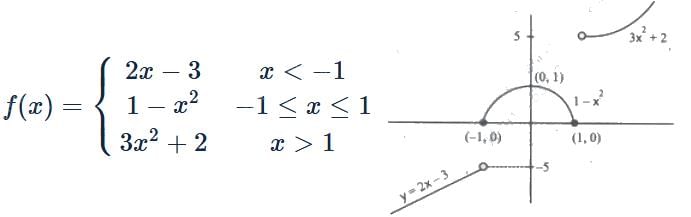
Formation of the differential equation of the family of curves represented by y = Ae2x + Be-2x is :



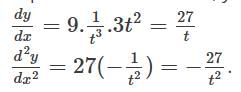
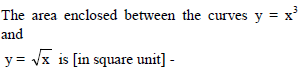
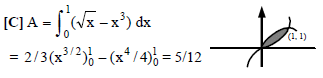



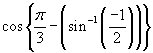 is given by
is given by


 , then
, then