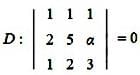
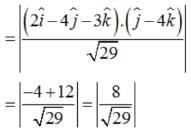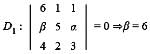Given the differential equation:
y'' + 9y = 0
We need to find which function satisfies this equation.
Step 1: Test each option by calculating y'' + 9y
Option A: y = 5 tan 3x
-
y = 5 tan 3x
-
y' = 5 * 3 sec² 3x = 15 sec² 3x
-
y'' = 15 * derivative of sec² 3x = 15 * 2 sec² 3x * tan 3x * 3 = 90 sec² 3x tan 3x (using chain rule)
Now, y'' + 9y = 90 sec² 3x tan 3x + 9 * 5 tan 3x = tan 3x (90 sec² 3x + 45) which is not zero for all x.
Option A does not satisfy the equation.
Option B: y = 5 cos 3x
-
First derivative: y' = 5 * (-3 sin 3x) = -15 sin 3x
-
Second derivative: y'' = -15 * 3 cos 3x = -45 cos 3x
Now, compute y'' + 9y:
y'' + 9y = -45 cos 3x + 9 * 5 cos 3x = -45 cos 3x + 45 cos 3x = 0
So, Option B satisfies the differential equation.
Option C: y = cos 3x
-
y' = -3 sin 3x
-
y'' = -9 cos 3x
Compute y'' + 9y:
-9 cos 3x + 9 cos 3x = 0
Option C satisfies the equation.
Option D: y = 6 cos 3x
-
y' = -18 sin 3x
-
y'' = -54 cos 3x
Compute y'' + 9y:
-54 cos 3x + 9 * 6 cos 3x = -54 cos 3x + 54 cos 3x = 0
Option D satisfies the equation.
Final answer:
Options B, C, and D satisfy the differential equation y'' + 9y = 0.
Among the given choices,
B: y = 5 cos 3x
C: y = cos 3x
D: y = 6 cos 3x
are solutions.
Only Option A is not a solution.


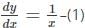
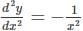
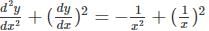
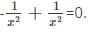

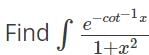

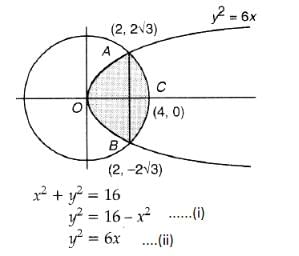

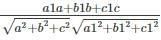
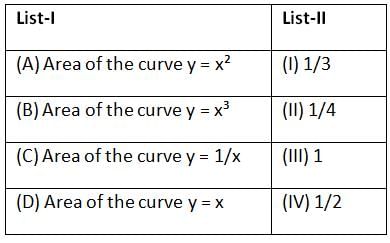
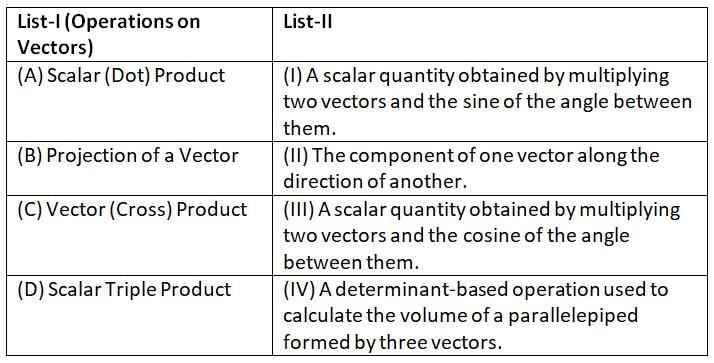
 is.
is.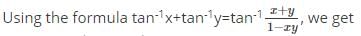
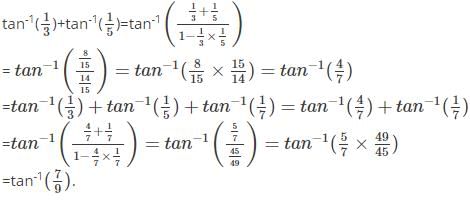
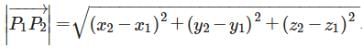
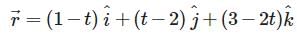 and
and