Mathematics: CUET Mock Test - 5 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 5
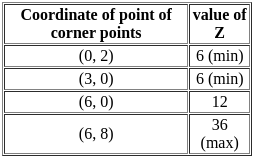
Corner points of the feasible region for an LPP, are (0, 2), (3, 0), (6, 0) and (6, 8). If z = 2x + 3y is the objective function of LPP then max. (z)-min.(z) is equal to:
Differential equation representing the family of curves given by y = ax + x2 is:
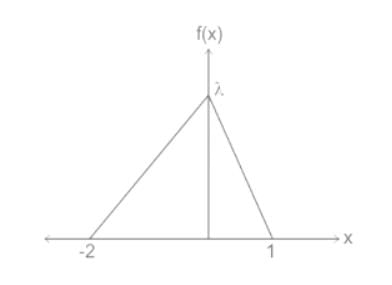
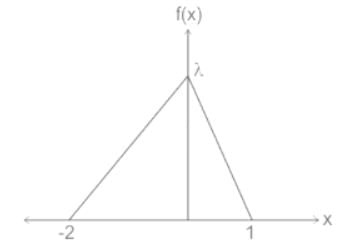
The graph of the probability density function of a random variable X is shown below. What should be the value of λ for this probability density function to be valid?
Find the distance travelled by a car moving with acceleration given by a(t)=Sin(t), if it moves from t = 0 sec to t = π/2 sec, and velocity of the car at t=0sec is 10 km/hr.
Formation of the differential equation corresponding to the ellipse major axis 2a and minor axis 2b is:
The steps followed for the development of linear programming model are
1. state of problem in the form of a linear programming model
2. determine the decision variables
3. write the objective function
4. develop inequations (or equations) for the constraints.
The correct order is
There are 4 white and 4 black balls in a bag and 3 balls are drawn at random. If balls of same colour are identical, the probability that none of them is black, is-
What is the length of the perpendicular drawn from point (3, 4, 5) to line 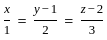 ?
?
If cosines of angles made by vector with coordinate axes are l, m and n then which option is correct?
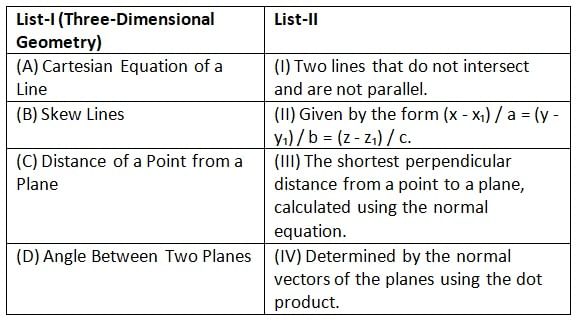
Choose the correct answer from the options given below:
If the order of the matrix is m×n, then how many elements will there be in the matrix?
Does Rolle’s theorem applicable if f(a) is not equal to f(b)?
Another form of Rolle’s theorem for the continuous condition is _____
The matrix which follows the conditions m=n is called?
What is the relation between f(a) and f(b) according to Rolle’s theorem?
What is the mathematical expression for the definition of continuity on (a,b)?


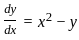 ?
?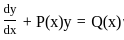 is given by
is given by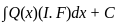
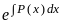
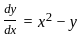 ⇒
⇒ 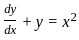
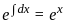
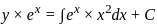
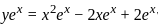
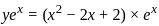
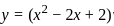

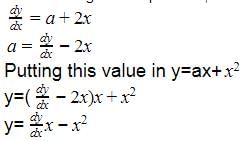
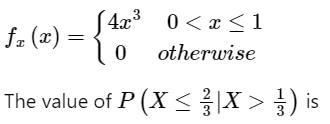
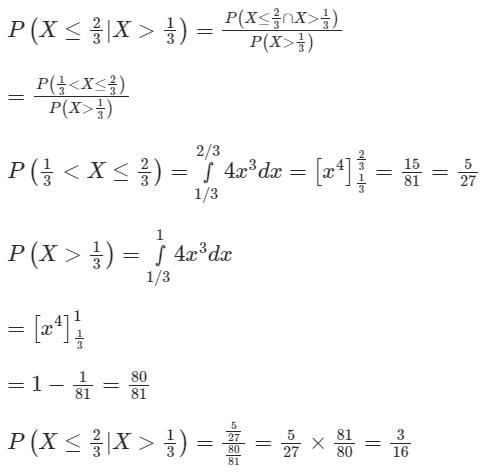
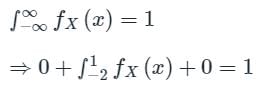
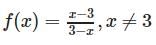 is
is 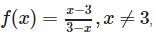
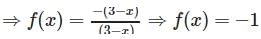
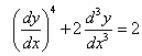
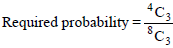
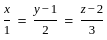 and point (3, 4, 5)
and point (3, 4, 5)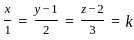
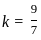
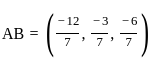

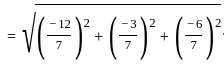
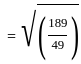
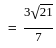
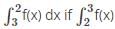 = 4.
= 4.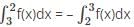
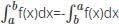 ?
?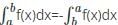 .
.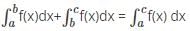
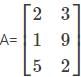 ?
?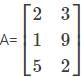 has 3 rows and 2 columns. Therefore, the order of the matrix is 3×2.
has 3 rows and 2 columns. Therefore, the order of the matrix is 3×2.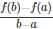 .
.










