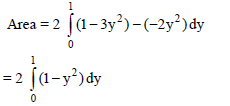Mathematics: CUET Mock Test - 6 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 6
The probability that a person stopping at a gas station will ask to have his tyres checked is 0.12, the probability that he will ask to have his oil checked is 0.29 and the probability that he will ask to have them both checked is 0.07. The probability that a person who has his tyres checked will also have oil checked is
If the order of the matrix is m×n, then how many elements will there be in the matrix?
The matrix which follows the conditions m=n is called?
Match List-I with List-II:
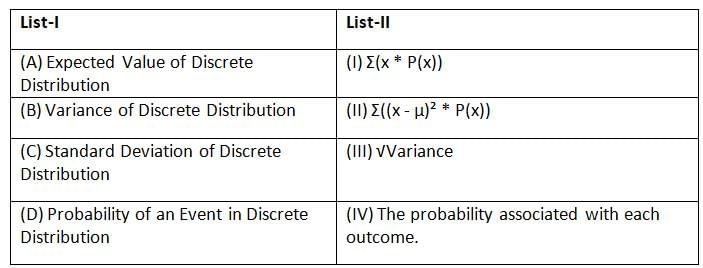
Choose the correct answer from the options given below:
Which of the following matrices will not have a determinant?
Which of the following is a matrix of the order 2×2 where the equation of the elements is given by aij =i+j.
Consider the matrix A= 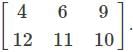 What is the type of matrix?
What is the type of matrix?
Which of the following relations is symmetric but neither reflexive nor transitive for a set A = {1, 2, 3}.
Which of the following relations is transitive but not reflexive for the set S={3, 4, 6}?
Which one is correct, the following system of linear equations 2x – 3y + 4z = 7, 3x – 4y + 5z = 8, 4x – 5y + 6z = 9 has?
Which of the following matrix is of the order 4x3.
Find the value of k if the area of the triangle is 7/2 sq. units and the vertices are (1,2), (3,5), (k,0).
Which of the following relations is symmetric and transitive but not reflexive for the set I = {4, 5}?
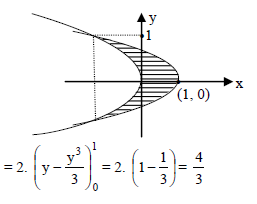
The area of the plane region bounded by the curves x + 2y2 = 0 and x + 3y2 = 1 is equal to-
Identify the form of the given Differential Equation
Consider the following linear programming problem:Maximize Z = 2A + 3B, subject to:A + B ≤ 10,4A + 6B ≤ 30,2A + B ≤ 17,A ≥ 0, B ≥ 0.What can one say about the solution?


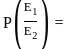 Probability o fgetting the event E1 when E2 is already occured.
Probability o fgetting the event E1 when E2 is already occured.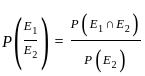
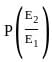 = Probability of person who has his tyre checked will also have oil checked
= Probability of person who has his tyre checked will also have oil checked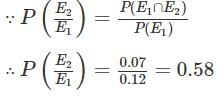
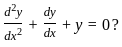
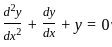

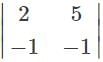 .
.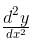 in terms of y
in terms of y

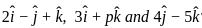 are coplanar then value of p is ?
are coplanar then value of p is ?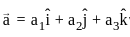 ,
, 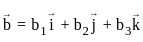 and
and 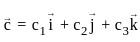 , then
, then 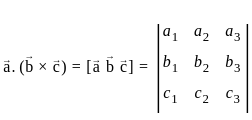 .
.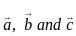 vectors are coplanar then
vectors are coplanar then 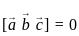
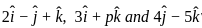 are coplanar.
are coplanar.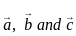 vectors are coplanar then
vectors are coplanar then 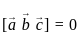
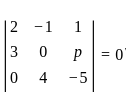
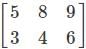 is not possible as it is a rectangular matrix and not a square matrix. Determinants can be calculated only if the matrix is a square matrix.
is not possible as it is a rectangular matrix and not a square matrix. Determinants can be calculated only if the matrix is a square matrix.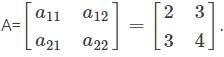
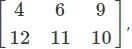 m = 3 and n = 2 i.e.
m = 3 and n = 2 i.e.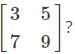
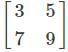 is 2. Therefore, the order of the matrix is 2×2(m×n).
is 2. Therefore, the order of the matrix is 2×2(m×n). is ____
is ____ is of the order 3×1. The matrix has only one column (n=1). Hence, it is a column matrix.
is of the order 3×1. The matrix has only one column (n=1). Hence, it is a column matrix.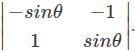

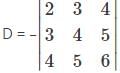
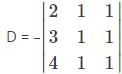

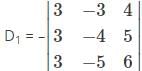
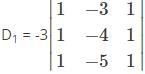
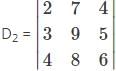
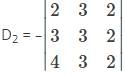
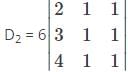
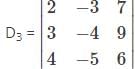
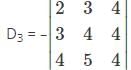


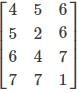 is a 4×3 matrix as it as 4 rows and 3 columns.
is a 4×3 matrix as it as 4 rows and 3 columns.