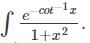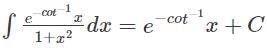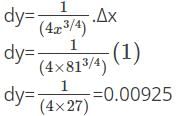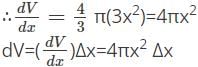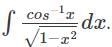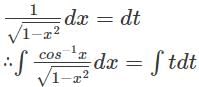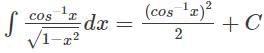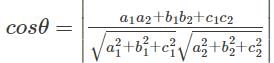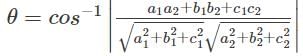Mathematics: CUET Mock Test - 9 - CUET MCQ
30 Questions MCQ Test - Mathematics: CUET Mock Test - 9
If I3 is the identity matrix of order 3 , then 13−1 is
The order of the differential equation of all tangent lines to the parabola y = x2 is
The maximum value of z = 4x + 2y subject to constraints
2x + 3y ≤ 28
x + y ≤ 10
x, y ≥ 0 is
If f: (0, π) → R is given by (x)=∑nk=1 [1 + sin kx], [x] denotes the greatest integer function, then the range of f(x) is
Let A = {a, b, c} and R = {(a, a), (b, b), (c, c), (b, c)} be a relation on A. Here, R is
The number of solutions of the equation sin-1 x - cos-1 x = sin-1(1/2) is
If A = 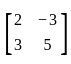 , then which of the following statements are correct?
, then which of the following statements are correct?
A. A is a square matrix
B. A−1 exists
C. A is a symmetric matrix
D. |A| = 19
E. A is a null matrix
Choose the correct answer from the options given below.
For which of the elements in the determinant Δ= 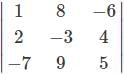 the cofactor is -37.
the cofactor is -37.
A 5 ft long man walks away from the foot of a 12(½) ft high lamp post at the rate of 3 mph. What will be the rate at which the shadow increases?
Find the approximate error in the volume of the sphere if the radius of the sphere is measured to be 6cm with an error of 0.07cm.
A particle moving in a straight line covers a distance of x cm in t second, where x = t3 + 6t2 – 15t + 18. What will be the velocity of the particle at the end of 2 seconds?
If L1 and L2 have the direction ratios a1,b1,c1 and a2,b2,c2 respectively then what is the angle between the lines?
Match List-I with List-II:
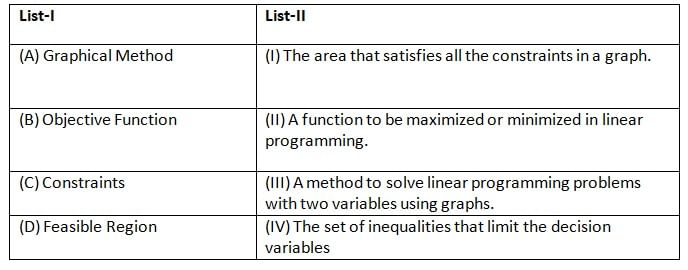
Choose the correct answer from the options given below:
Match List-I with List-II:
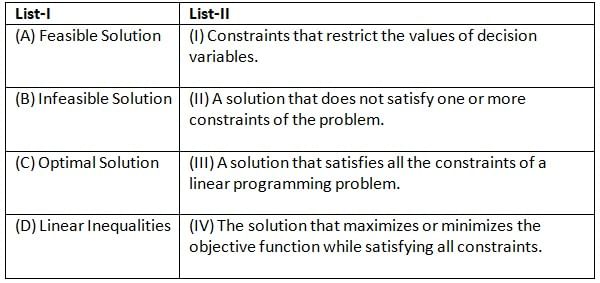
Choose the correct answer from the options given below:
Match List-I with List-II:
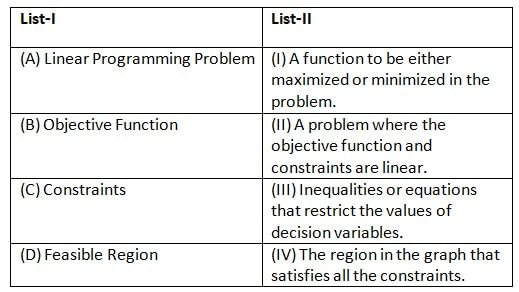
Choose the correct answer from the options given below:



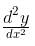
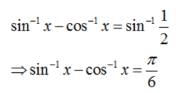
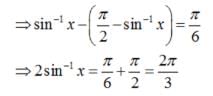
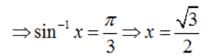
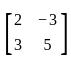 , we can see, the number of rows and columns are 2 respectively. Since the order of the matrix is 2 × 2, hence A is a square matrix.
, we can see, the number of rows and columns are 2 respectively. Since the order of the matrix is 2 × 2, hence A is a square matrix.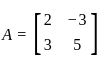
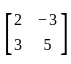 then AT =
then AT = 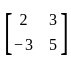
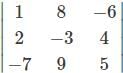
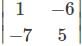 =1(5)-(-6)(-7)=5-42=-37
=1(5)-(-6)(-7)=5-42=-37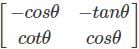 .
.
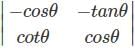
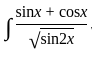
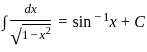
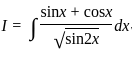 . . .(1)
. . .(1)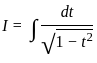
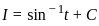

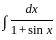 equals
equals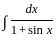
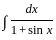 ×
× 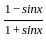 dx
dx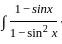 ...(1 - sin2x = cos2x)
...(1 - sin2x = cos2x)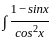 =
=