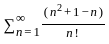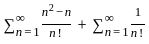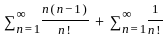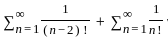TN TRB PG Assistant Mock Test- 4 (Mathematics) - TN TET MCQ
30 Questions MCQ Test - TN TRB PG Assistant Mock Test- 4 (Mathematics)
The particular integral of (d³y/dx³) - 3(d²y/dx²) + 4y = e³ˣ is
The solution of the differential equation y = px + √(4 + p²) is
If 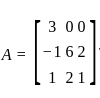 and B = 4 A2, then the det (B) will be:
and B = 4 A2, then the det (B) will be:
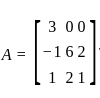 and B = 4 A2, then the det (B) will be:
and B = 4 A2, then the det (B) will be:∫ eˣ {f(x) + f'(x)} dx is equal to:
If a function f(z) is continuous at Z = Z0, then which of the following statements does not hold?
Equation (α xy3 + y cos x) dx + (x2y2 + β sin x) dy = 0 is exact if
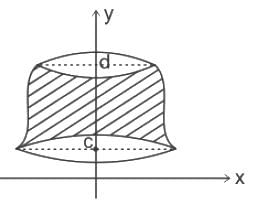
The volume generated by revolving the arc 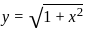 lying between x = 0 and x = 4 about x - axis is
lying between x = 0 and x = 4 about x - axis is
For the subset S = {(1, 0, 0), (0, 1, 0), (0, 0, ), (1, 1, 1), (1, 1, 0)} in ℝ3 which of the following is (/are) correct:.
(A) S is a linearly dependent set.
(B) Any three vectors of S are linearly independent.
(C) Any four vectors of S are linearly dependent.
Choose the correct answer from the options given below:
If 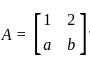 & the product of A and its transpose is
& the product of A and its transpose is  then value of a & b is respectively is
then value of a & b is respectively is
Find the cardinality of generating set for dihedral group?
If f(z) is an analytic function within and on a simple closed contour C and a is any point inside C, then the integral  is equivalent to:
is equivalent to:
List - I consists of double integrals and List - II consists of double integrals after changing the order of integration.
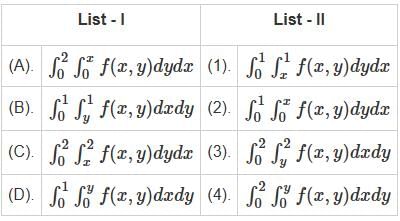
Choose the correct answer from the options given below:
Consider the following statements where X and Y are nxn matrices with real entries then which of the following is(/ are) correct::
(A) If P-1XP is diagonal matrix for some real invertible matrix P, then there exists a basis for Rn consisting of eigenvectors of X.
(B) If X is diagonal matrix with distinct diagonal entries and XY = YX, then Y is also diagonal matrix.
(C) If X2 is diagonal matrix, then X is diagonal matrix.
(D) If X is diagonal matrix and XY = YX for all Y, then X = λ| for some λ ∈ R
Choose the correct answer from the options given below
The function 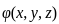 = xy + yz + az is a potential for the vector field
= xy + yz + az is a potential for the vector field 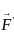 =
=
(A) 
(B) 
(C) 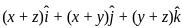
Choose the correct answer from the options given below:
If A = 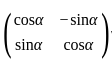 and A + A' = I, then the value of α is
and A + A' = I, then the value of α is
The solution of the differential equation 2x (dy/dx) - y = 3 represents a family of
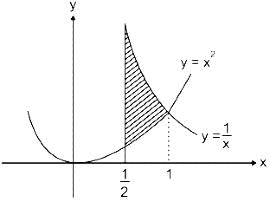
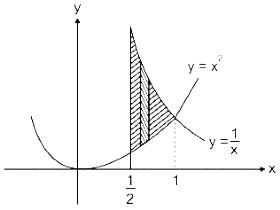
Find the area of the region bounded by the curves y = x², y = 1/x, and x = 1/2 (see in the graphical represented figure).
a⃗ = 2î + ĵ + 3k̂ and b⃗ = 3î - 2ĵ + k̂ are two vectors. The angle between them is:
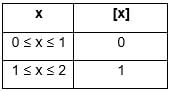
The number of points at which the function f(x) = 1 / (x - [x]) is not continuous is
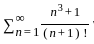 then which of the following is correct?
then which of the following is correct?
Statement (B): It focused exclusively on medical education to address healthcare needs in the region.




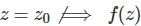
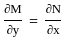
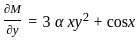
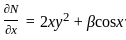
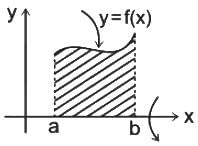
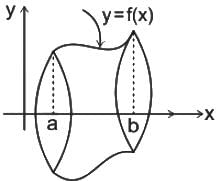
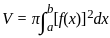
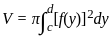
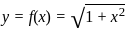 and a = 0, b =
and a = 0, b =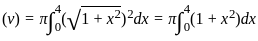
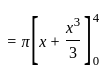
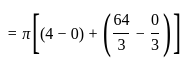
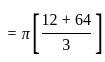
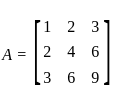

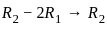
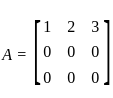
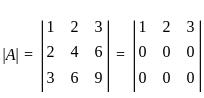
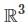
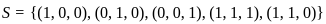
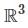 , and the maximum number of linearly independent vectors in
, and the maximum number of linearly independent vectors in 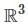 is 3, the set must be linearly dependent.
is 3, the set must be linearly dependent.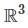 , any 4 vectors must be linearly dependent because the rank of the matrix formed by these vectors is at most 3
, any 4 vectors must be linearly dependent because the rank of the matrix formed by these vectors is at most 3
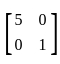
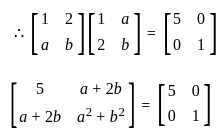

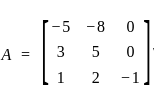
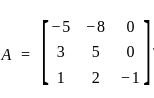
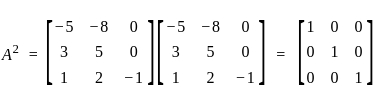
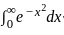 is:
is: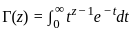
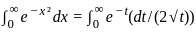

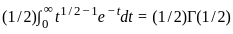
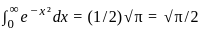
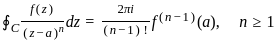
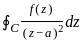
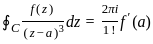
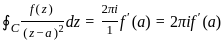
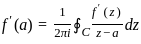
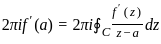
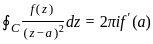 ,
,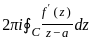

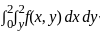
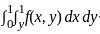
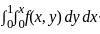
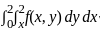
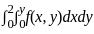
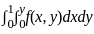
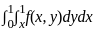
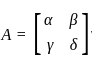 , then find the adj A:
, then find the adj A: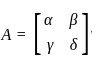
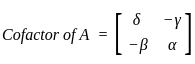
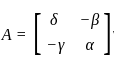
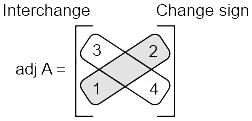
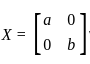
 (diagonal values are different)
(diagonal values are different)
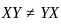
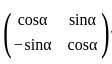 where,
where, 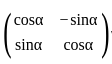
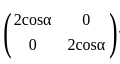 =
= 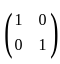
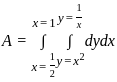
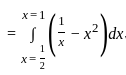
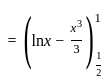
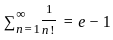 and
and