JEE Main Maths Test- 8 - JEE MCQ
Test Description
25 Questions MCQ Test - JEE Main Maths Test- 8
JEE Main Maths Test- 8 for JEE 2025 is part of JEE preparation. The JEE Main Maths Test- 8 questions and answers have been prepared
according to the JEE exam syllabus.The JEE Main Maths Test- 8 MCQs are made for JEE 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for JEE Main Maths Test- 8 below.
Solutions of JEE Main Maths Test- 8 questions in English are available as part of our course for JEE & JEE Main Maths Test- 8 solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt JEE Main Maths Test- 8 | 25 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Detailed Solution for JEE Main Maths Test- 8 - Question 2
JEE Main Maths Test- 8 - Question 10
If a,b,c are respectively the pth,qth and rth terms of an H.P., then 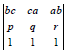
JEE Main Maths Test- 8 - Question 11
If x,y,z (>0) are the pth, qth rth terms of a G.P. then the determinant
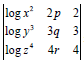 is
is
JEE Main Maths Test- 8 - Question 14
If be the determinant given in last question and
=0 then system of lines given by the equation ax by c=0 pass through the point
JEE Main Maths Test- 8 - Question 15
If the three digit numbers A28,3B9, and62C where A,B and C are integers between 0 and 9 which are divisible by 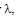 the D =
the D = 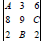 is divisible by
is divisible by
JEE Main Maths Test- 8 - Question 16
if 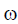 is imaginary cube root of unity then the value of
is imaginary cube root of unity then the value of 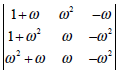 is equal to
is equal to
Detailed Solution for JEE Main Maths Test- 8 - Question 16
Detailed Solution for JEE Main Maths Test- 8 - Question 17
*Multiple options can be correct
JEE Main Maths Test- 8 - Question 18
The value of lying between
=0 and
and satisfying then equation
are
Detailed Solution for JEE Main Maths Test- 8 - Question 18
JEE Main Maths Test- 8 - Question 19
If A is any m×n matrix such that AB and BA are both defined, then B is a matrix of type
JEE Main Maths Test- 8 - Question 20
If a matrix has 13 elements, then the possible dimensions (order) it can have are
*Answer can only contain numeric values
Detailed Solution for JEE Main Maths Test- 8 - Question 21
*Answer can only contain numeric values
JEE Main Maths Test- 8 - Question 22
If y = cos θ + sin θ and 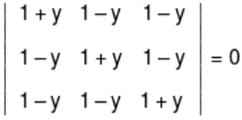 then numbers of values of θ ∈ [0, 2π] is
then numbers of values of θ ∈ [0, 2π] is
Detailed Solution for JEE Main Maths Test- 8 - Question 22
*Answer can only contain numeric values
Detailed Solution for JEE Main Maths Test- 8 - Question 23
*Answer can only contain numeric values
Detailed Solution for JEE Main Maths Test- 8 - Question 24
*Answer can only contain numeric values
Information about JEE Main Maths Test- 8 Page
In this test you can find the Exam questions for JEE Main Maths Test- 8 solved & explained in the simplest way possible.
Besides giving Questions and answers for JEE Main Maths Test- 8, EduRev gives you an ample number of Online tests for practice
Download as PDF





 then r is equal to
then r is equal to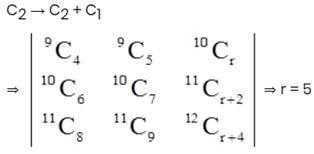
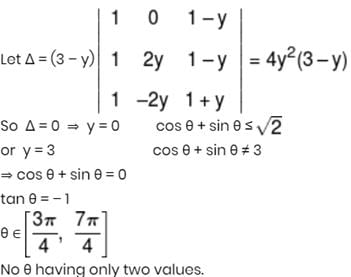
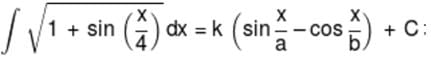 then value of (k + a + b) = ?
then value of (k + a + b) = ?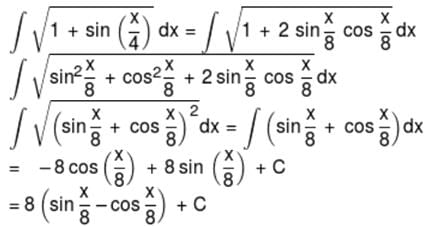
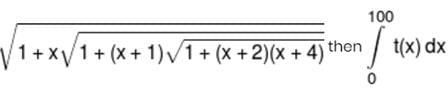 is
is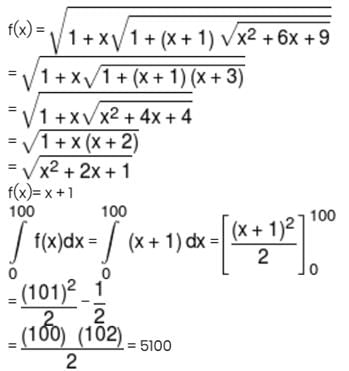
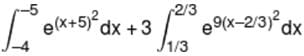 is
is















