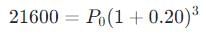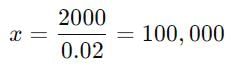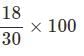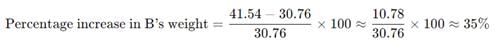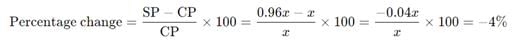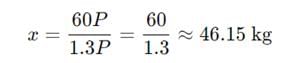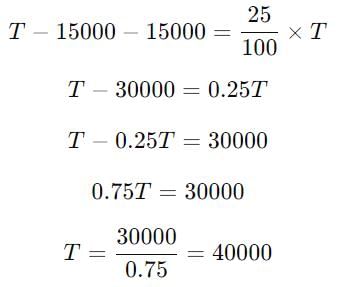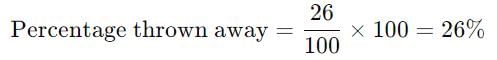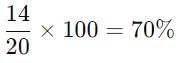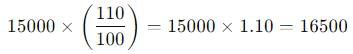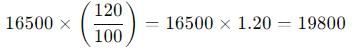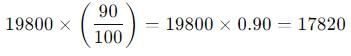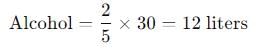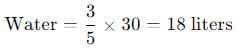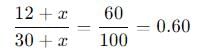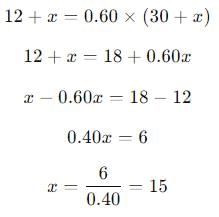Percentage - MCQ 3 - Railways MCQ
20 Questions MCQ Test - Percentage - MCQ 3
A reduction of 20% in the price of rice enables a housewife to buy 5 kg more for rupees 1200. The reduced price per kg of rice
The population of a village has increased annually at the rate of 20%. If at the end of 3 years it is 21600, the population in the beginning of the first year?
12 percent of the voters in an election did not cast their votes. In this election there are only two candidates. The winner by obtaining 45% of the total votes and defeated his rival by 2000 votes. The total number of votes in the election
A number is first decreased by 25%. The decreased number is then increased by 20%. The resulting number is less than the original number by 40. Then the original number is –
The number of seats in a cinema hall is decreased by 8% and also the price of the ticket is increased by 4 percent. What is the effect on the revenue collected?
Ashwin distributes 30 sweets between Shweta and pallavi in the ratio 2 : 3. How much percentage of sweets do Pallavi get?
Weights of two friends A and B are in the ratio of 1 : 2. A’s weight increases by 20% and the total weight of A and B together becomes 60 kg, with an increase of 30%. By what percent the weight of B increase?
The marked price of an article is 20% higher than the cost price. A discount of 20% is given on the marked price. In this transaction the seller
When the price of rice is increased by 30 percent, a family reduces its consumption such that the expenditure is only 20 percent more than before. If 50 kg of rice is consumed by family before, then find the new consumption of family (approx.)
A man has 4000 rupees in his account two years ago. In the first year he deposited 20 percent of the amount in his account. In the next year he deposited 10 percent of the increased amount in the account. Find the total amount in the account of the person after 2 years.
In an election contested by two parties A and B, party A secured 25 percent of the total votes more than Party B. If party B gets 15000 votes. By how much votes does party B loses the election?
A vendor sells 50 percent of apples he had and throws away 20 percent of the remainder. Next day he sells 60 percent of the remainder and throws away the rest. What percent of his apples does the vendor throw?
40% of the women are above 30 years of age and 80 percent of the women are less than or equal to 50 years of age. 20 percent of all women play basketball. If 30 percent of the women above the age of 50 play basketball, what percent of players are less than or equal to 50 years?
Alisha goes to a supermarket and bought things worth rupees 60, out of which 40 paise went on sales tax. If the tax rate is 10 percent, then what was the cost of tax free items?
60 percent of the employees of a company are women and 75% of the women earn 20000 or more in a month. Total number of employees who earns more than 20000 per month in the company is 60 percent of the total employees.What fraction of men earns less than 20000 per month?
In a library, 30% of the books are in History. 50% of the remaining are in English and 40% of the remaining are in German. The remaining 4200 books are in regional languages. What is the total number of books in library?
A got 30% of the maximum marks in an examination and failed by 10 marks.However, B who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What were the passing marks in the examination?
The population of a town is 15000. It increases by 10 percent in the first year and 20 percent in the second year. But in the third year it decreases by 10 percent. What will be the population after 3 years.
30 litre of solution contains alcohol and water in the ratio 2:3. How much alcohol must be added to the solution to make a solution containing 60% of alcohol?
720 sweets are distributed equally among the children in such a way that the number of sweets given to each child is equal to 20% of the total number of children. How many sweets did each child get?