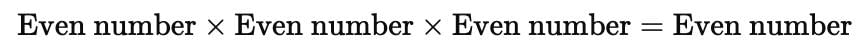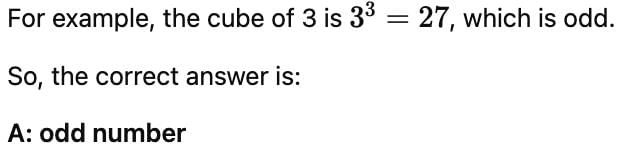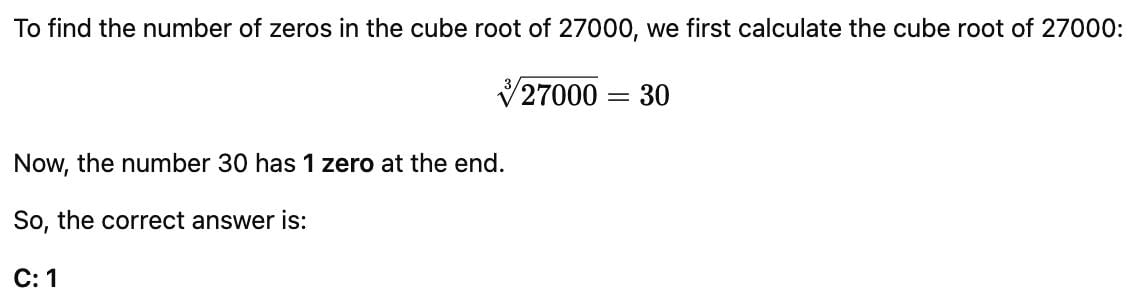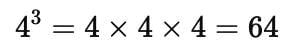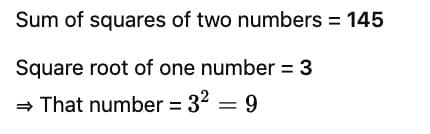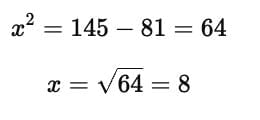Test: A Square and A Cube - 1 - Class 8 MCQ
30 Questions MCQ Test - Test: A Square and A Cube - 1
What will be the unit digit of the cube of a number ending with 6 ?
What will be the unit digit of the cube of a number ending with 2 ?
The number of digits in the cube root of a 6-digit number is _______.
The smallest natural number by which 135 must be divided to obtain a perfect cube is
How many zeros will be there in the cube root of 800?
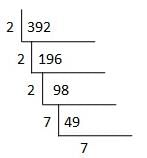
By which smallest natural number 392 must be multiplied so as to make the product a perfect cube ?
How many zeros will be there in the cube root of 27000?
What will be the unit digit of the cube of a number ending with 4 ?
For a number ending with 7, the unit digit of its cube is equal to:
The smallest natural number by which 704 must be divided to obtain a perfect cube is
What will be the unit digit of the cube root of a number ends with 2?
Sum of squares of two numbers is 145. If square root of one number is 3, find the other number.
What will be the number of zeros in the square of the number 100?
If 5278 is squared, then what will be at unit place?