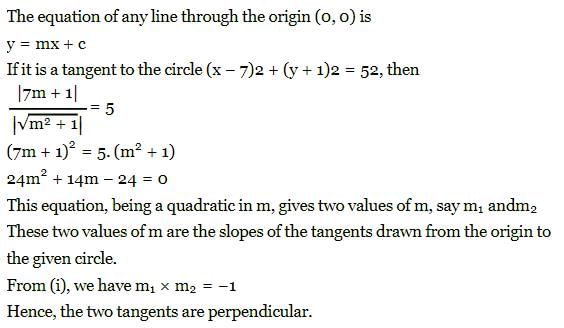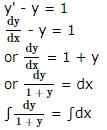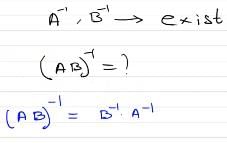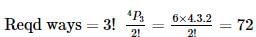BITSAT Maths Test - 5 - JEE MCQ

The limiting point of the system of co-axial circles x²+y²-6x-6y+4=0, x²+y²-2x-4y+3=0 is

The differential equation for the family of curves x² + y² - 2ay = 0, where a is an arbitrary constant is

If [(1 + i√3)/(1 + i√3)]ⁿ is an integer ,then n is equal to

The general solution of the equation x²(dy/dx)=2 is

The solution of y'- y = 1, y(0) = 1 is given by y (x)

The number of points at which the function f(x)=|x-0.5|+|x-1|+tanx is not differentiable in (0,2) is

Sum of the infinite series 1 + 3/2! + 6/3! + 10/4! + ...... is

If y = sec tan^⁻1 x, then (dy/dx) =

If a flag staff of 6 mt high placed on the top of a tower throws a shadow of 2 √3 mt along the ground then the angle that the sun makes with the ground is

A variable straight line of slope 4 intersects the hyperbola xy = 1 at two points. The locus of the point which divides the line segment between these two points in the ratio 1:2 is

The general solution of the differential equation (dy/dx) = (x²/y²) is

The area bounded by the curve y² = 9x and the lines x = 1, x = 4 and y = 0 in the first quadrant is

Let f(x + y) = f(x)f(y) for all x and y. Suppose that f(3) = 3 and f′(0) = 11 then f′(3) is given by

A square matrix can always be expressed as a

If A and B are square matrices and A^⁻1 and B^⁻1 of same order exists, then (AB)^⁻1 is equal to

The curved surface of the cone inscribed in a given sphere is maximum if h=

If z is a complex number, then | 3z − 1 | = 3 | z − 2 | represents

The angle between lines given by x²+4y²-7xy=0 is

If x+y+1=0 tocuhes the parabola y²=λx,then λ is equal to

The line y=mx+c touches the parabola x²=4ay if

How many words are formed from the letters of the word EAMCET so that two vowels are never together?

Number of triangles formed by joining 12 points, no three of which are in the same straight line except 7 of them which are in a straight line, is

The mean and variance of a Binomial distribution are 6 and 4. The parameter n is

Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is

In