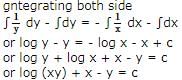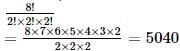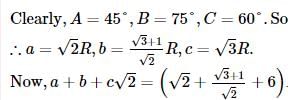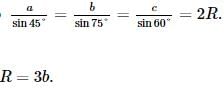BITSAT Maths Test Free Online Test 2026

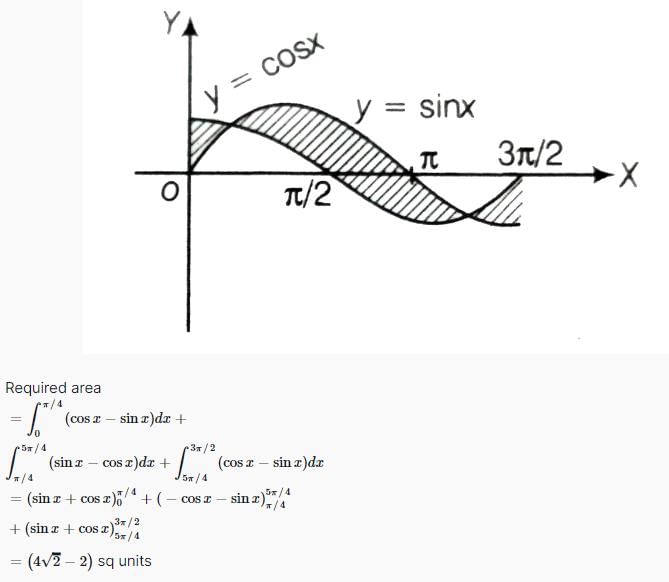
The area of the figure bounded by the curves y = cos x and y = sin x and the ordinates x = 0 and x = 3π/2 is

The sum of the coefficients in the expansion of (1+x-3x²)³¹⁴⁸ is

The equation of a circle which is ortho gonal to circles x²+y²+3x-5y+6=0 and 4x²+4y²-28x+29=0 and whose centre lies on the line 3x+4y+1=0 is

The equation of circle which passes through the points (3,-2) and (-2,0) and whose centre lies on the line 2x-y-3=0 is

The least positive integral value of n for which

The differential equation for the family of curves x² + y² - 2ay = 0, where a is an arbitrary constant is

The solution of differential equation

(d/dx)[tan^⁻1((sinx+cosx)/(cosx-sinx))]

Differential of sin^⁻1[(1-x)/(1+x)] w.r. to √x is equal to

1/2! - 1/3! + 1/4! - 1/5! + ....... equals

From the top of a building of height h metres, the angle of depression of an object on the ground is α. The distance (in metres) of the object from the foot of the building is

The product of the perpendicular, drawn from any point on a hyperbola to its asymptotes is

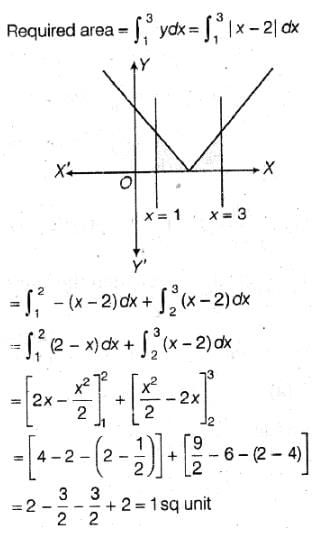
The area of the region bounded by the curves y = |x-2|, x = 1, x = 3 and the x-axis is

The solution of the equation x(dy/dx)=y-xtan(y/x) is

The differential equation (d²y/dx²)^2/3 = (y + dy/dx)^1/2 is of

The sum of first 50 terms of the series cot^⁻1 3 + cot^⁻1 7 + cot^⁻1 13 + cot^⁻1 21 + ... is

The function f(x) = cot^⁻1x + x increases in the interval

(1/1)+(1/(1+2))+(1/(1+2+3))+...up to (n+1) terms is equal to

If B is a non-singular matrix and A is a square matrix, then det (B^⁻1 AB) is equal to

If in a square matrix A=[a_ij], we find that
a_ij = a_ji ∀ i,j, then A is a

The complex numbers 1,-1, i √3 from a triangle which is

If the function f(x) = 2x³ - 9ax² + 12a²x + 1, where a > 0, attains its max. and min. at p and q respectively such that p² = q then a equals

The locus of the point of intersection of two normals to the parabola x²=8y, which are at right angles to each other,is

Each line represented by equation (x₁y-xy₁)²=a²(x²+y²) is at a distance from (x₁,y₁)

If the normal at the point t on a parabola y = 4ax meet it again at t₁, then t₁ =

The number of words formed from the letters of the word INDEPENDENCE when vowels are together is

The numbers of all words formed from the letters of the word CALCUTTA is

A problem in mathematics is given to 3 students whose chances of solving individually are 1/2, 1/3, and 1/4. The probability that the problem will be solved atleast by one is

The mean and variance of a Binomial distribution are 6 and 4. The parameter n is

In a ΔABC , A : B : C = 3 : 5 : 4 . Then a + b + c √2 is equal to