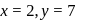VITEEE Maths Test - 1 - JEE MCQ
30 Questions MCQ Test - VITEEE Maths Test - 1
If 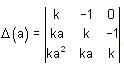 , then which of the following terms will completely divide Δ (2a) - Δ(a)?
, then which of the following terms will completely divide Δ (2a) - Δ(a)?
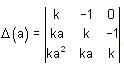 , then which of the following terms will completely divide Δ (2a) - Δ(a)?
, then which of the following terms will completely divide Δ (2a) - Δ(a)? The probability of getting heads in both trials when a balanced coin is tossed twice, will be
Find the maximum number of points of intersection of 8 circles.
The curve described parametrically by x = t2 + 2t − 1, y = 3t + 5 represents
If the sum of first n natural numbers is one-fifth of the sum of their squares, then n is
If a polygon has 44 diagonals, then the number of its sides are
If 7 points out of 12 are in same striaght line, then the number of triangles formed is
Ram is moving away from a tower at the rate of 2.3 m/sec. If the height of the tower is 5.6 m and Ram's height is 190 cm, find the rate at which his shadow is increasing and the tip of his shadow is moving.
Two cards are drawn at random from a pack to 52 cards. The probability of these two being aces is
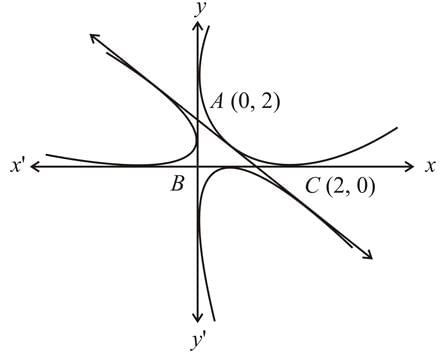
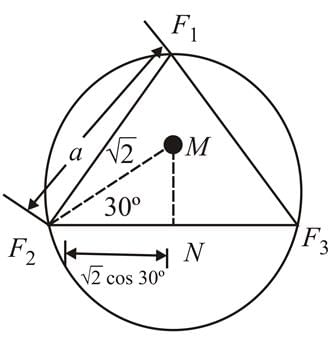
If three parabolas touch all the lines x=0, y=0 and x+y=2, then the maximum area of the triangle formed by joining their foci is
If all the words formed from the letters of the word "HORROR" are arranged in the opposite order as they are in a dictionary, then the rank of the word "HORROR" is
Two tangents are drawn from a point (-2, -1) to the curve y2 = 4x. If α is the angle between them, then |tanα| is equal to
If A is a square matrix such that (A − 2I)(A + I) = O, then (A + 2I) =
Out of 6 boys and 4 girls, a group of 7 is to be formed. In how many ways can this be done, if the group is to have a majority of boys?
The sum of 40 terms of an A.P. whose first term is 2 and common difference 4, will be
The equation of a line is 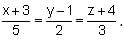 If a perpendicular is drawn at the line from the point P(2, 4, 6), the coordinates of the foot of the perpendicular are
If a perpendicular is drawn at the line from the point P(2, 4, 6), the coordinates of the foot of the perpendicular are
There were two women participating in a chess tournament. Every participant played two games with the other participants. The number of games that the men played between themselves proved to exceed by 66 the number of games that the men played with the women. The number of participants is
The shortest distance (in units) between the parabolas y2 = 4x and y2=2x−6 is
A force 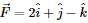 acts at a point A whose position vector is
acts at a point A whose position vector is 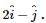 If point of application of
If point of application of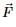 moves from A to the point B with position vector
moves from A to the point B with position vector 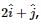 then work done by
then work done by 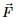 is
is


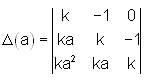

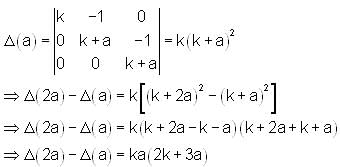
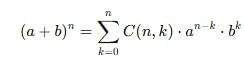


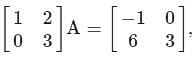 then what is A equal to?
then what is A equal to?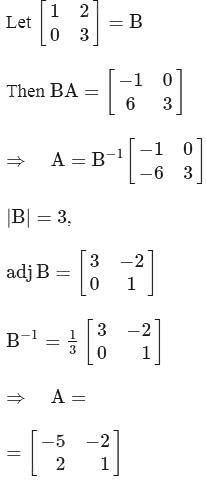
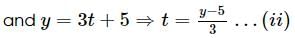
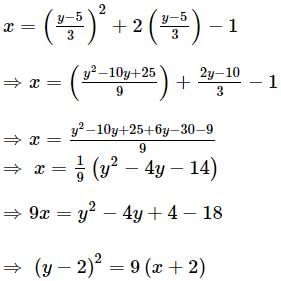

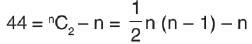
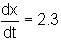 is the rate at which Ram is moving away from the post.
is the rate at which Ram is moving away from the post.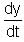 is the rate at which Ram's shadow is increasing.
is the rate at which Ram's shadow is increasing.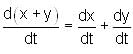 is the rate at which the tip of the shadow is moving
is the rate at which the tip of the shadow is moving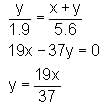
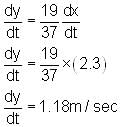
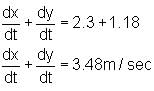
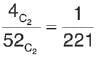
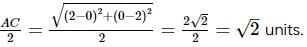
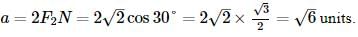
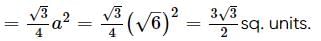
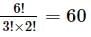



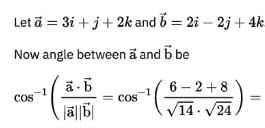
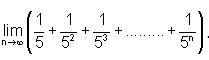
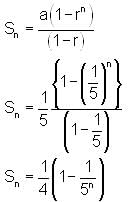

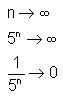
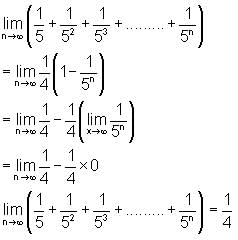
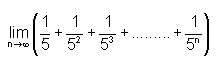
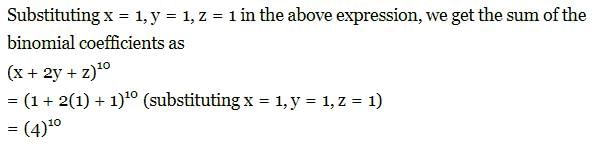
 is a scalar and
is a scalar and  is a unit matrix of order 3 , then
is a unit matrix of order 3 , then 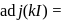

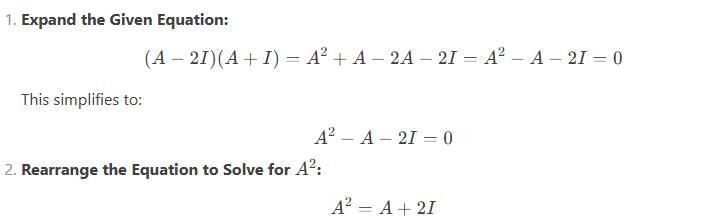
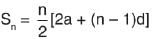

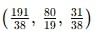
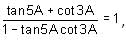 then find the general solution for A.
then find the general solution for A.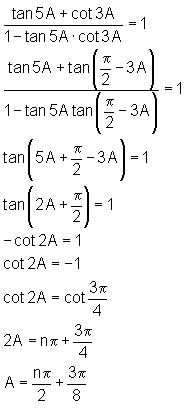
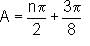
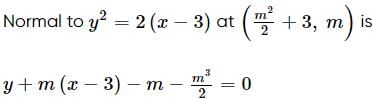
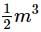
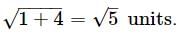
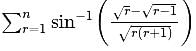 is equal to
is equal to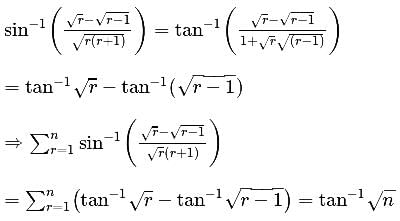
 ve integral solution of
ve integral solution of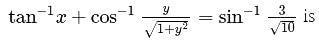
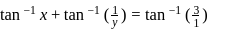
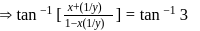
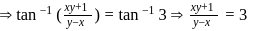
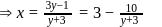
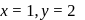 and for
and for