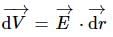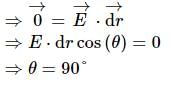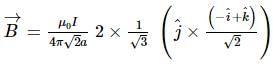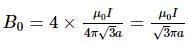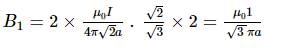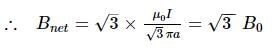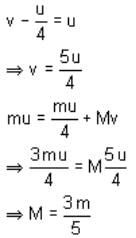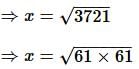VITEEE PCME Mock Test - 10 - JEE MCQ
30 Questions MCQ Test - VITEEE PCME Mock Test - 10
The perpendicular distance of point (2, -1, 4) from the line  lies between
lies between
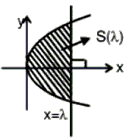
Let f(x, y) = {(x, y) : y2 ≤ 4x, 0 ≤ x ≤ λ} and S(λ) is area such that S(λ)/S(4) = 2/5. Find the value of λ.
If common chord of circles x2 + y2 + 5kx + 2y + k = 0 and x2 + y2 + kx +  = 0 is 4x - 5y - k = 0 then number of values of k is
= 0 is 4x - 5y - k = 0 then number of values of k is
Consider the following statements and answer accordingly:
Statement - I: (p ∧ ~q) ∧ (~p ∧ q) is a fallacy.
Statement - II: (p → q) ↔ (~q → ~p) is tautology.
Both the roots of the quadratic equation (x − a)(x − b) + (x − c)(x − a) + (x − b)(x − c) = 0 are always _____
If f(x) = |sin x| and g(x) = x³, then identify which of the following is correct for the function f(g(x)).
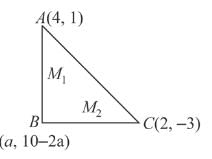
The vertex of the right angle of a right-angled triangle lies on the straight line 2x + y − 10 = 0, and the two other vertices are at the points (2, −3) and (5, 3). The area of the triangle in square units is:
Let A(2,3,5), B(-1,3,2), and C(λ,5,μ) be the vertices of triangle ABC. If the median through A is equally inclined to the coordinate axes, then the correct equation is:
The given expression is: nC0 - nC₁ + nC₂ - nC₃ + … + (−1)ʳ ⋅ nCᵣ = 28 Then n is equal to:
What is the distance of a focus of the ellipse 9x2 + 16y2 = 144 from an end of the minor axis?

A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T, normal to the plane of the coil. If the current in the coil is 5 A, then the torque acting on the coil will be:
The angle between the electric field and an equipotential surface will always be:
Assertion: If two long parallel wires, hanging freely are connected to a battery in series, they come closer to each other.
Reason: Force of attraction acts between the two wires carrying current.
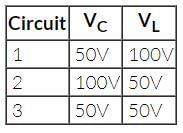
The table shows the rms voltage VC across the capacitor and the rms voltage VL across the inductor for three series RCL circuits. In which circuit does the rms voltage across the entire RCL combination lead the current through the combination?
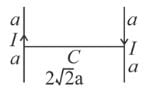
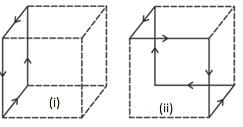
If magnetic field due to current I in figure (i) at the centre of cube is B, then magnetic field due to current I at the centre of the same cube in figure (ii) is
An object A of mass m with initial velocity u collides with a stationary object B. After elastic collision A moves with u/4. Calculate mass of B.
In amplitude modulation equation of messenger wave A0 sin ωmt and carrier wave Ac cos ωct, the equation of amplitude modulated wave is
In the preparation of HNO3, we get NO gas by catalytic oxidation of ammonia. The number of moles of NO produced by the oxidation of two moles of NH3 will be ____. (in integer)
Native silver metal forms a water-soluble complex with a dilute aqueous solution of NaCN in the presence of
Which of the following lanthanoid ions are coloured?
(a) Lu+3
(b) Pm+3
(c) Sm+3
(d) Eu+3
In the question given below, a part of the sentence has been underlined. Below are given alternatives for the underlined part which may improve the sentence. Choose the alternative which makes the sentence grammatically and contextually correct. In case the sentence is correct as it is, choose 'No Improvement' as your answer.
Avarice was Shylock's chief trait of character.
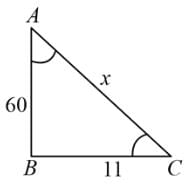
A ladder is resting with one end in contact with the top of a wall of height 60 m and the other end on the ground is at a distance of 11 m from the wall. The length of the ladder is:


 .
. 


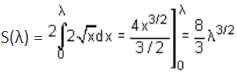





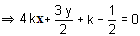
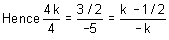
 and k2 +
and k2 + 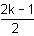 = 0
= 0

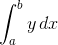
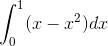


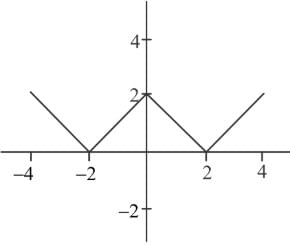
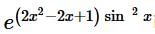 is:
is: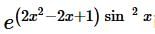
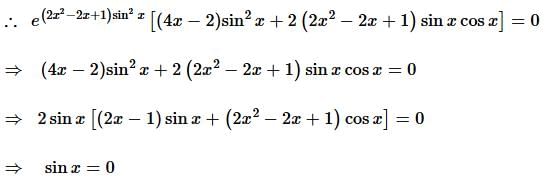
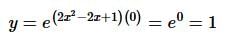
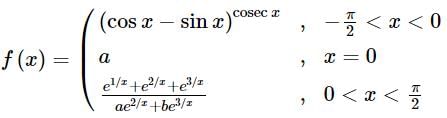 then
then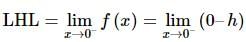 =
= 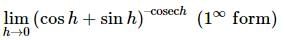
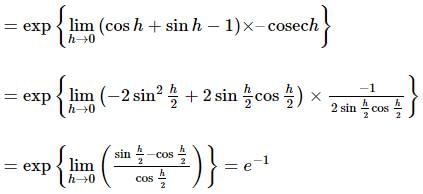
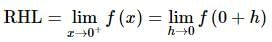

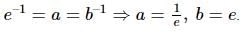

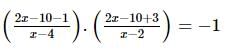
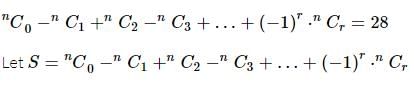
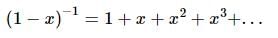
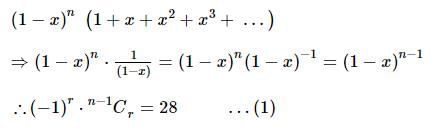
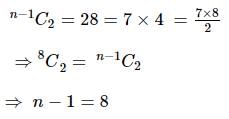
 = 1
= 1 = 1 – e2
= 1 – e2 e2 = 1 -
e2 = 1 - 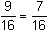
 e =
e = 
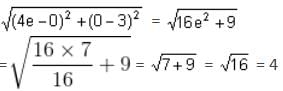
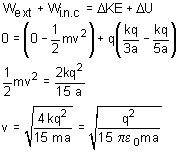
 , where f is the focal length, n is the refractive index and R1 and R2 are the radii of curvatures.
, where f is the focal length, n is the refractive index and R1 and R2 are the radii of curvatures. and n = 1.6.
and n = 1.6.
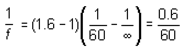
 f = 100 cm.
f = 100 cm.