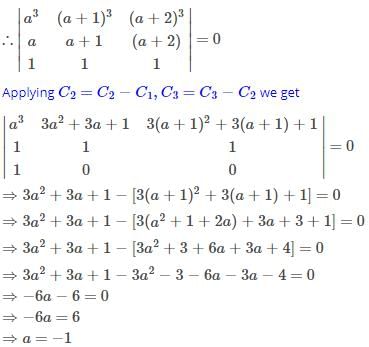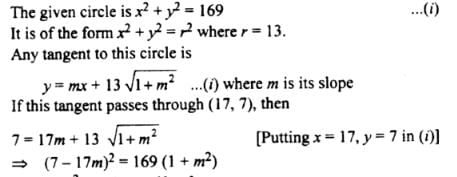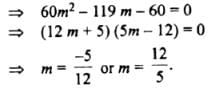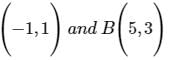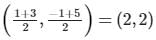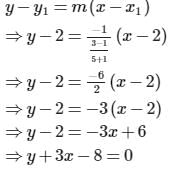JEE Main Maths Mock Test- 1 - JEE MCQ
25 Questions MCQ Test - JEE Main Maths Mock Test- 1
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A):If Cr is the coefficient of xr in the expansion of (1 + x)20
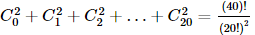
Reason(R) : Cr = Cn − r for any positive integer n
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A) :The inverse of  does not exist.
does not exist.
Reason(R) :The matrix is non singular.
Assertion(A) :The inverse of
Reason(R) :The matrix is non singular.
If the line 3x-4y=λ touches the circle x2+y2-4x-8y-5=0, λ can have the values
The area (in square units) bounded by the curves y2 = 4x and x2 = 4y in the plane is
The length of the tangent from (0,0) to the circle 2x2 + 2y2 + 7x -7 y + 5 = 0 is
The differential equation which represents the family of plane curves y=exp. (cx) is
The fundamental period of the function f(x) = 2 cos 1/3(x - π) is
Consider the planes 3x – 6y – 2z = 15 and 2x + y – 2z = 5.
Statement-1:
The parametric equations of the line of intersection of the given planes are
x = 3 + 14t, y = 1 + 2t, z = 15t.
Statement-2:
The vector 14î+2ĵ+15k̂ is parallel to the line of intersection of given planes
The value of a for which the system of equations
a3x+(a+1)3y+(a+2)3z = 0
ax+(a+1)y+(a+2)z = 0
x+y+z = 0
has a non-zero solution, is
In the following question, a Statement-1 is given followed by a corresponding Statement-2 just below it. Read the statements carefully and mark the correct answer-
Tangents are drawn from the point (17,7) to the circle x2+y2=169.
Statement-1:
The tangents are mutually perpendicular.
Statement-2:
The locus of the points from which mutually perpendicular tangents can be drawn to the given circle is x2+y2=338.
The pole of the line 2x + 3y − 4 = 0 with respect to the parabola y2 = 4 x is
The two opposite vertices of a square on xy-plane are A(-1,1) and B(5,3), the equation of other diagonal (not passing through A and B) is
If the normal to the curve y=f(x) at the point (3,4) makes an angle 3π/4 with the positive x-axis, then f'(3)
If f (x) = a cos (bx + c) + d, then what is the range of f (x)?
Assume e-4/5 = 2/5. If x, y satisfy, y = ex and the minimum value of (x2 + y2) is expressed in the form of m/n then (2m - n)/5 equals (where m & n are coprime natural numbers)
Let ƒ(x) be non-constant thrice differentiable function defined on (–∞, ∞) such that ƒ(x) = ƒ(6 – x) and ƒ'(0) = 0 = ƒ'(2) = ƒ'(5). If 'n' is the minimum number of roots of (ƒ"(x))2 + ƒ'(x)ƒ"'(x) = 0 in the interval x ∈ [0, 6] then sum of digits of n equals
If a, b, c, x, y, z are non-zero real numbers and 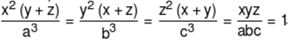 then the value of (a3 + b3 + c3 + abc) equals
then the value of (a3 + b3 + c3 + abc) equals
If the co-ordinate of the vertex of the parabola whose parametric equation is x = t2 – t + 1 and y = t2 + t + 1, t ∈ R is (a, b) then (2a + 4b) equals