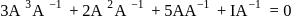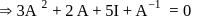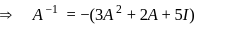SRMJEEE Maths Mock Test - 2 - JEE MCQ
30 Questions MCQ Test - SRMJEEE Maths Mock Test - 2
If the area of a Δ A B C be λ then a2 sin 2B + b2 sin 2A is equal to
The radius of the circle in which the sphere x2 + y2 + z2 + 2x - 2y - 4z - 19 = 0 is cut by the plane x + 2y + 2z + 7 = 0, is
The pole of the line lx+my+n=0 w.r.t. the parabloa y2 =4ax
The difference of an integer and its cube is divisible by
If A+B+C=180o, then [(tanA+tanB+tanC)/(tanA tanB tanC)]=
The area (in square units) of the region enclosed by the curves y = x2 and y = x3 is
In a Δ A B C , a = 1 and the perimeter is six times the AM of the sines of the angles. The measure of ∠ A is
if A is a 3 x 3 matrix and B is its adjoint matrix. If ∣B∣ = 64, then ∣A∣ =
If x dy = y(dx + y dy), y > 0 and y (1) = 1, then y (-3) is equal to
Equation 2x2+7xy+3y2+8x+14y+λ=0 represents a pair of straight lines, value of λ is
In the expansion of (y1/6 - y-1/3)9 the term independent of y is :
The points with position vectors 10î + 3ĵ, 12î - 5ĵ and aî + 11ĵ are collinear if a =
A committee consists of 9 experts from three institutions A, B and C, of which 2 are from A, 3 from B and 4 from C. If three experts resign, then the probability that they belong to different institutions is
The number of vectors of unit length perpendicular to vectors 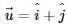 and
and 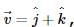 is
is
The sum of an infinite G.P. is 3. The sum of the series formed by squaring its terms is also 3. The series is
If the two circles 2x2 + 2y2 -3x + 6y + k = 0 and x2 + y2 - 4x + 10y + 16 = 0 cut orthogonally, then the value of k is
The equation line passing through the point P(1,2) whose portion cut by axes is bisected at P, is
The strength of a beam varies as the product of its breadth b and square of its depth d. A beam cut out of a circular log of radius r would be strong when
The equation of the common tangent to the curves y2=8x and xy=-1 is :
If α, β are the roots of the equation x2- 2x + 2 = 0, then the value of α2 + β2 is
The order and degree of differential equation √(dy/dx) - 4 (dy/ dx) - 7x = 0 are
How many total words can be formed from the letters of the word INSURANCE in which vowels are always together?
The 5th term of a G.P. is 2, then the product of its first 9 term is


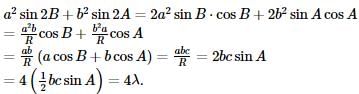


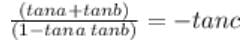
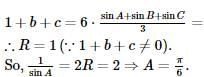
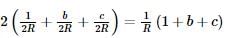
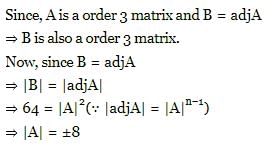
 and
and  are two square matrices such that
are two square matrices such that 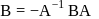 , then
, then 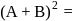
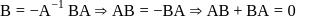
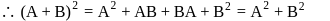
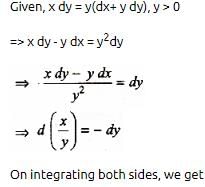
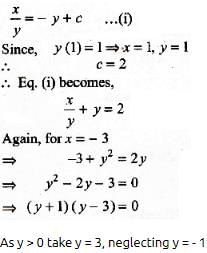
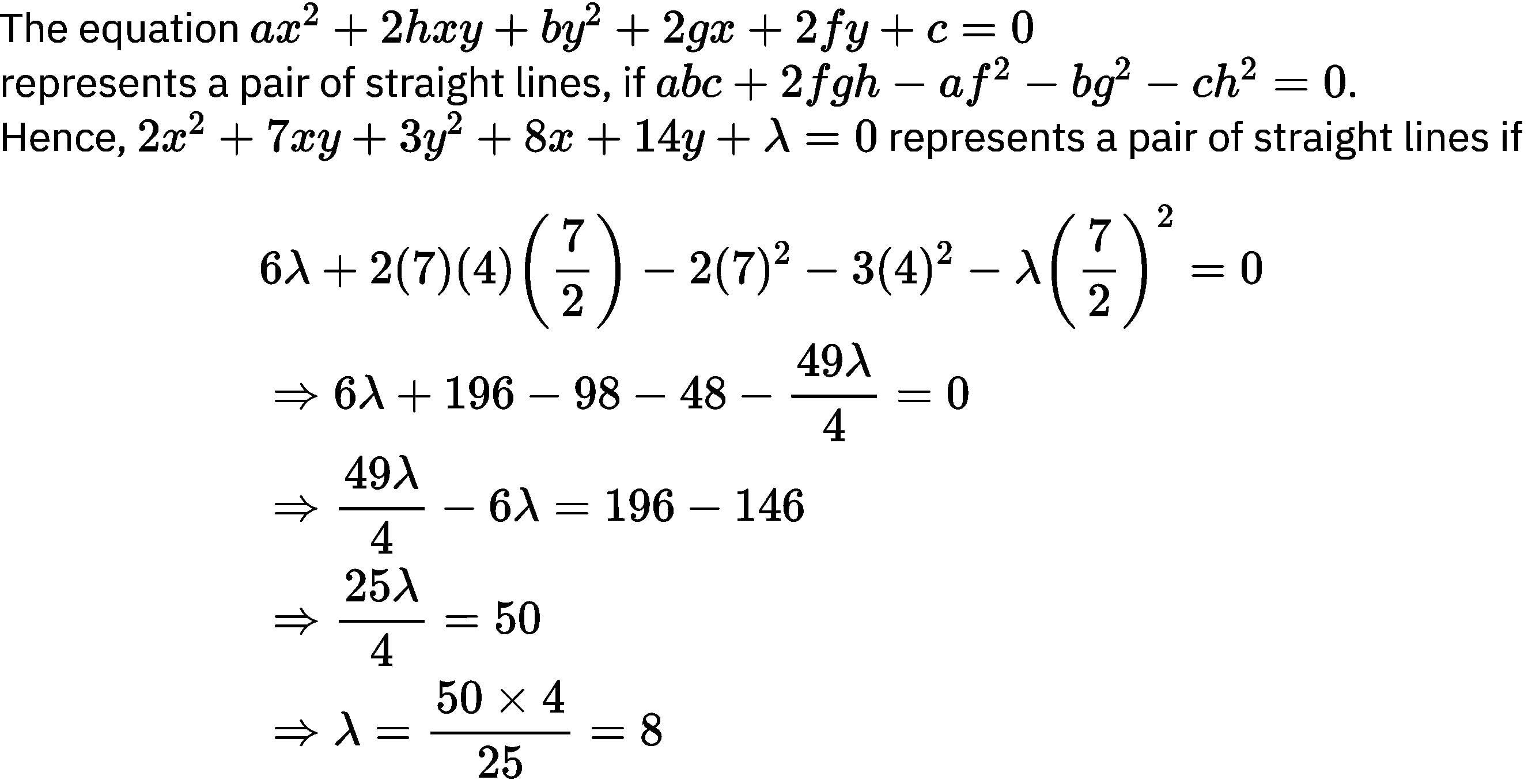

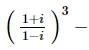
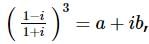 then a and b are
then a and b are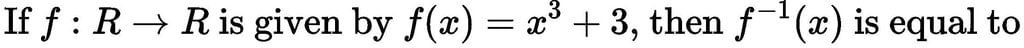
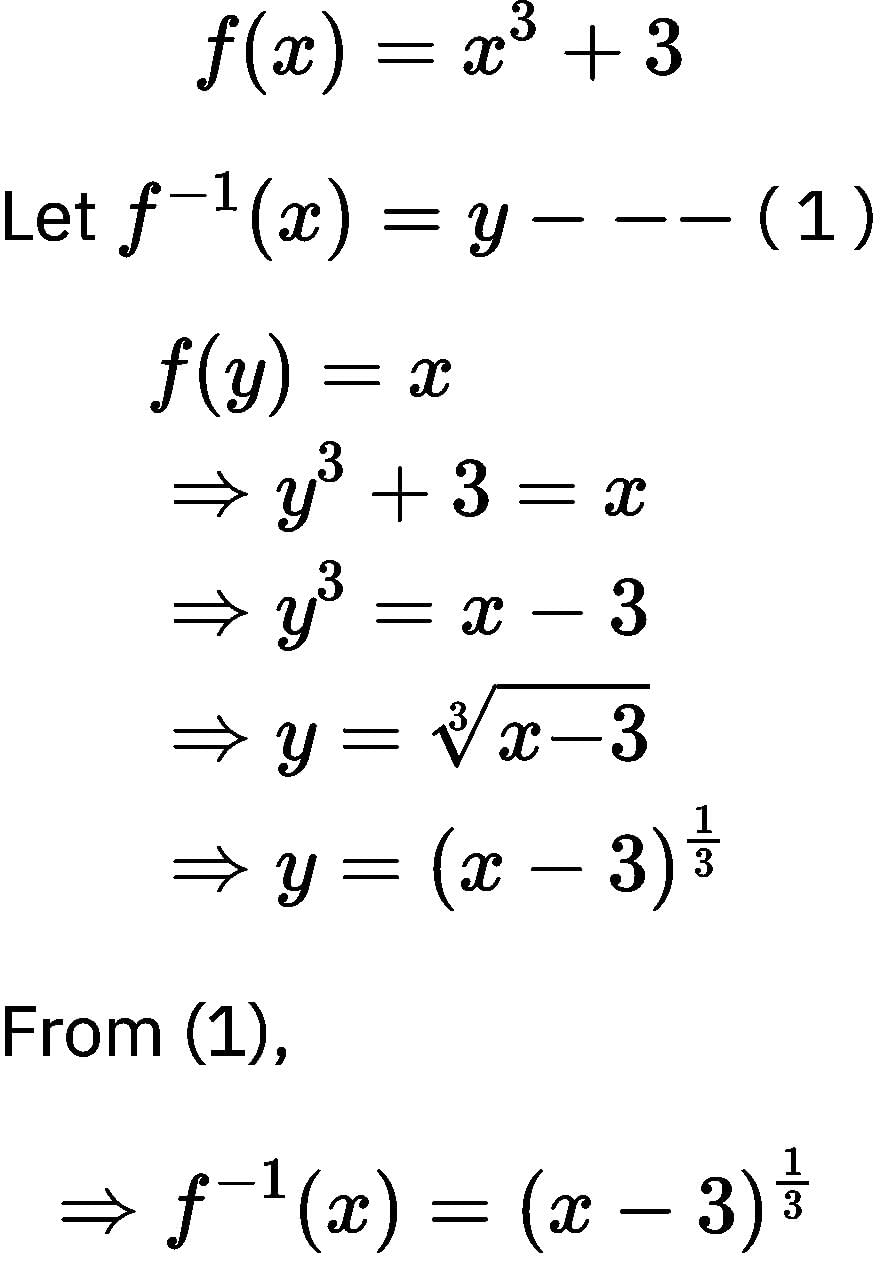
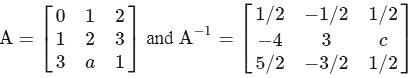 then the value of a + c is equal to
then the value of a + c is equal to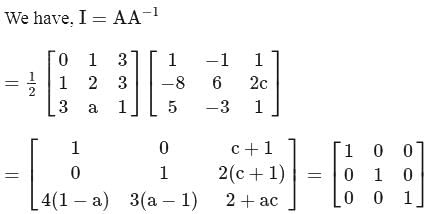

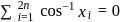 then
then 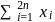 is
is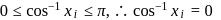 for all i.
for all i.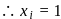 for all
for all 


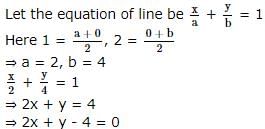
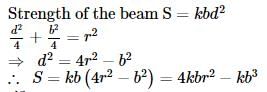
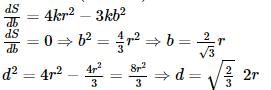

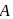 is such that
is such that 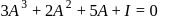
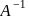 equal to?
equal to?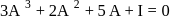
 on both the sides, we get
on both the sides, we get