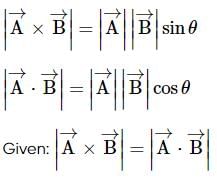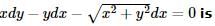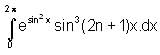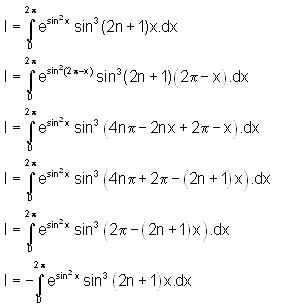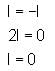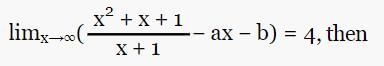SRMJEEE Maths Mock Test - 9 - JEE MCQ
30 Questions MCQ Test - SRMJEEE Maths Mock Test - 9
Consider the given expression:
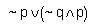
The negation of the above expression is
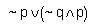
The locus of the point of intersection of two normals to the parabola x2=8y, which are at right angles to each other,is
If A and B are any 2 x 2 matrics, then |A + B| = 0 implies
The area common to the parabola y = 2x2 and y = x2 + 4 is
The length of the shadow of a rod inclined at 10o to the vertical towards the sun is 2.05 metres when the elevation of the sun is 38o.The length of the rod is
The area of the region bounded by the curve y = x - x2 between x = 0 and x = 1 is
A and B are square matrices of order n x n, then (A - B)2 is equal to
The equation of the line parallel to the tangent to the circle x2 + y2 = r2 at the point (x₁, y₁) and passing thro' origin is
If equation λx2 + 2y2 - 5xy + 5x - 7y + 3 = 0, represents two straight lines, the value of λ is
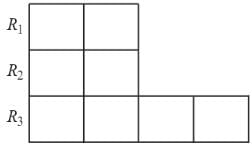
The number of ways in which we can put letters of the word PERSON in the squares of the Fig so that no row remains empty is
How many 5 digit telephone numbers can be constructed using the digits 0 to 9, if each number starts with 67 and no digit appears more than once?
If the co-ordinates of the points A,B,C be (−1, 3, 2), (2, 3, 5) and (3, 5,−2) respectively, then ∠A=
The orthocentre of the triangle with vertices (−2,−6), (−2,4) and (1,3) is
If two vectors 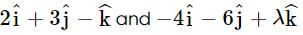 are parallel, then find the value of λ.
are parallel, then find the value of λ.
The value of b such that the scalar product of the vector î+ĵ+k̂ with the unit vector parallel to the sum of the vectors 2î + 4ĵ - 5k̂ and bî+ 2ĵ + 3k̂ is one is
Four normal dice are rolled once. The number of possible outcomes in which at least one die shows up 2 is -



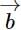 is a unit vector, then
is a unit vector, then 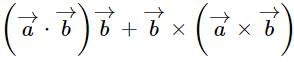 is
is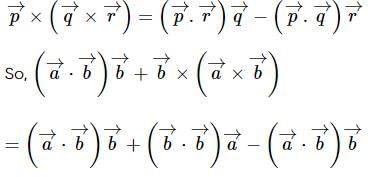
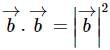
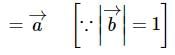

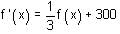 and f (0) = 300 , then find f(x).
and f (0) = 300 , then find f(x).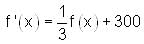
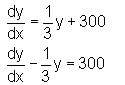
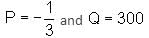
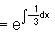
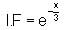
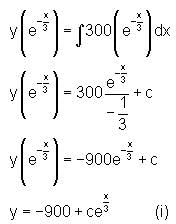
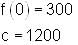
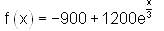
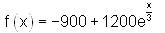

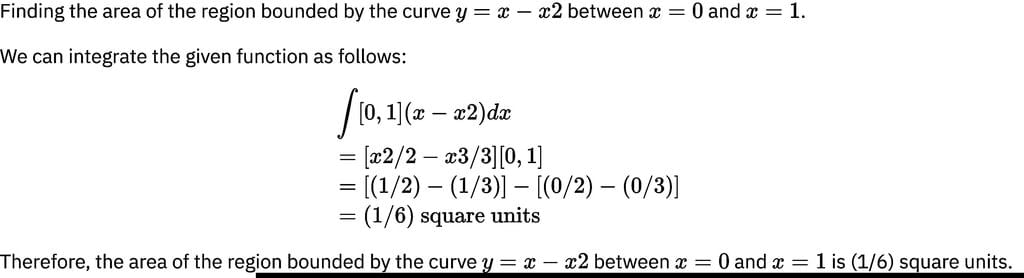
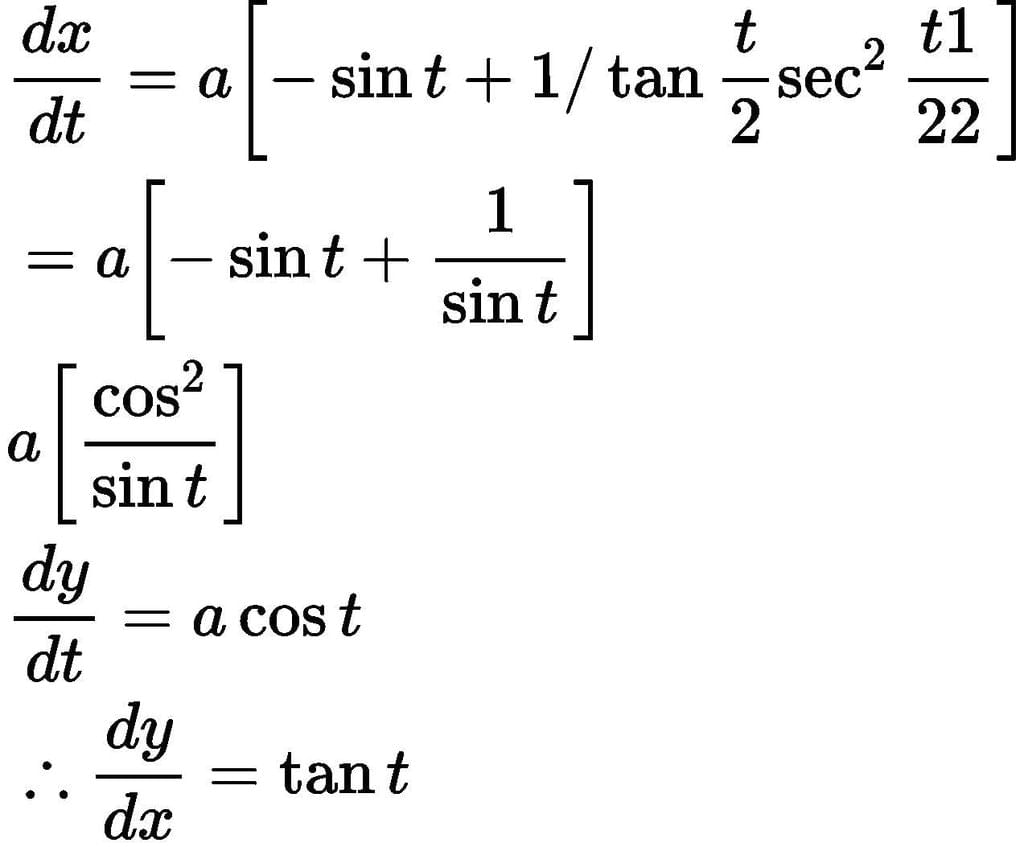
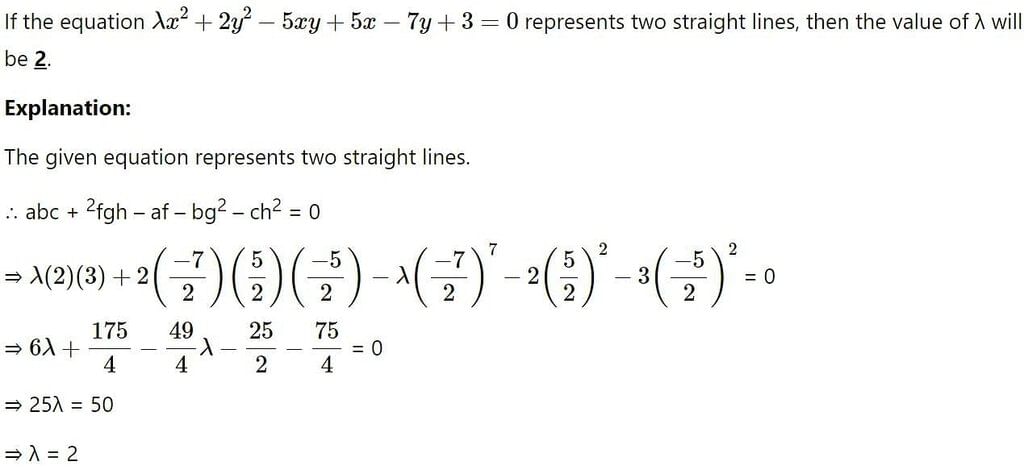
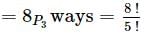
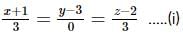
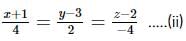
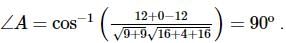
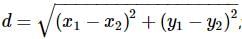 we get
we get 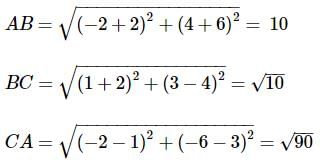
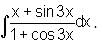
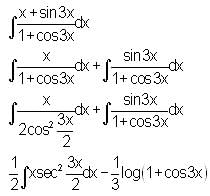
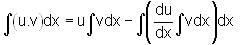
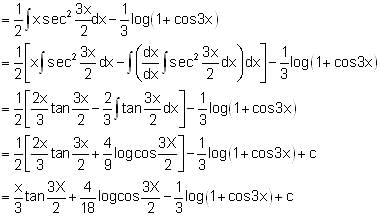
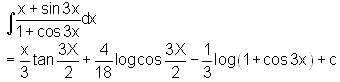
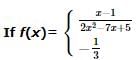
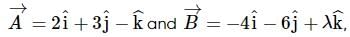 that are parallel to each other.
that are parallel to each other.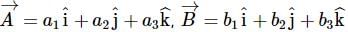 and if these vectors are parallel to each other, then they must follow,
and if these vectors are parallel to each other, then they must follow, 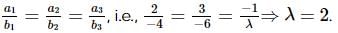
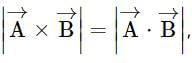 then angle between the vectors
then angle between the vectors  and
and is
is