Test: Inequalities - CA Foundation MCQ
30 Questions MCQ Test - Test: Inequalities
Find the range of real values of x satisfying the inequalities 3x-2 > 7 and 4x - 13 > 15
On the average, experienced person does 5 units of work while a fresh one 3 units work daily but the employer have to maintain the output of at least 30 units of work per day. The situation can be expressed as.
The Linear relationship between two variables in an inequality :
The union forbids employer to employ less than two experienced person (x) to each, fresh person (y). This situation can be expressed as:
Solution space of the inequalities 2x + y ≤ 10 and x - 7 ≤ 5:
(i) includes the origin.
(ii) includes the point (4,3)
which one is correct?
The graph of linear in equalities 7x + 9y ≤ 63, x + y ≥1, 0 ≤ x ≤ 6 and
On an average, experienced person does 5 units of work while a fresh person does 3 units of work daily but the employer has to maintain the output of atleast 30 units of work per day The situation can be expressed as.
The common region satisfying the set of inequalities x≥ 0, y ≥ 0 , L1 : x+ y ≤ 5, L2 : x + 2y ≤ 8 and L3: 4x+ 3y ≥ 12 is indicated by
By solving the inequality 3(a - 6) < 4 + a, the answer will be
The region indicated by the shading in the graph is expressed by inequalities
On solving the inequalities 6x+ y ≥ 18, x+4y ≥ 12, 2x+y ≥ 10, we get following situation
A car manufacturing company manufactures cars of two types A and B. Model A requires 150 man-hours for assembling, 50 man-hours for painting and 10 man-hours for checking and testing. Model B requires 60 man-hours for assembling, 40 man-hours for painting and 20 man-hours for checking and testing. There are available 30 thousand man-hours for assembling, 13 thousand man-hours for checking and testing. Express the above situation using linear inequalities. Let the company manufacture x units of type A model of car and y units type B model of car. Then, the inequalities are:
The set of inequalities L1 : x1 + x2 ? 12, L2: 5x1 + 2x2 ? 50, L3 : x1 + 3x2 ? 30, x1 ? 0 and x2 ? 0 is represented by
The common region indicated on the graph is expressed by the set of five inequalities
On solving the inequalities 6x + y ≥ 18, x + 4y ≥ 12, 2x + y≤ 10, we get the following situation:
Graphs of Inequations are drawn below:
L1 : 5x + 3y = 30 L2 : x+y = 9 L3 y = x/3 L4: y = x/2
The common region (shaded part) shown in the diagram refers to the inequalities:
A firm makes two types of products: Type A and Type B. The profit on product A is Rs. 20 each and that on product B is Rs. 30 each. Both types are processed on three machines M1, M2 and M3. The time required in hour by each product and total time available in hours per week on each machine are asa follows:
Machine Product A Product B Available Time
M1 3 3 36
M2 5 2 50
M3 2 6 60
The constraints can be formulated taking x1 = number of units A and x2 = number of unit of B as
The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one and this fact be expressed as
The common region satisfied by the inequalities L1 : 3x + y ≥ 6, L2 : x + y ≥ 4, L3: x + 3y ≥ 6, and L4: x + y ≤ 6 is indicated by
L1 : 5x + 3y = 30 L2 : x+y = 9 L3 : y = x/3 L4 : y = x/2
The common region (shaded part) shown in the diagram refers to
The region indicated by the shading in the graph is expressed by inequalities
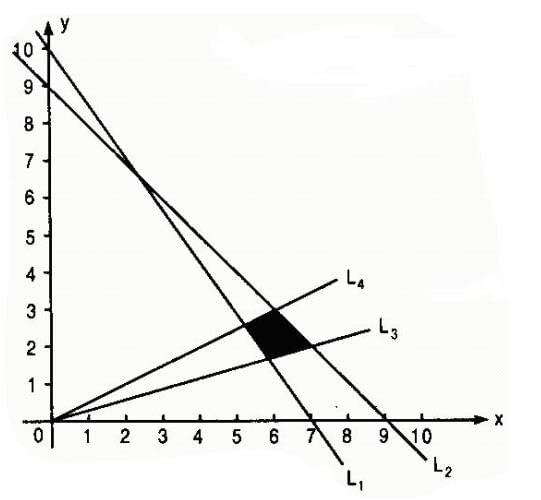
Graph of the inequations are below:
L1 : 2x + y = 9 L2 : x + y = 7 L3 : x + 2y = 10 L4: x + 3y = 12
The coomon region (shaded part) indicated on the diagram is expressed by the set of inequalities



















