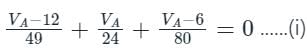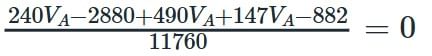Test: Mesh & Nodal Analysis - Electrical Engineering (EE) MCQ
20 Questions MCQ Test - Test: Mesh & Nodal Analysis
Find the value of the currents I1 and I2 flowing clockwise in the first and second mesh respectively.
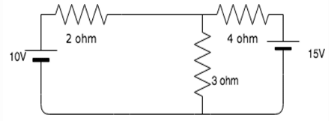
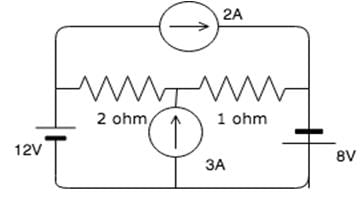
In the circuit shown below, the voltage and current sources are ideal. The voltage  across the current source, in volts, is
across the current source, in volts, is
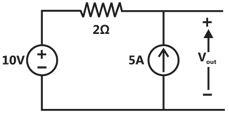
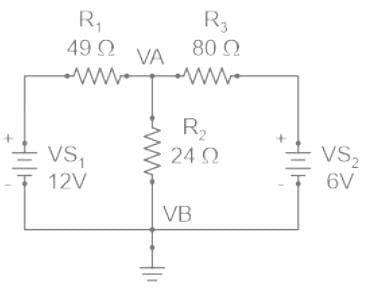
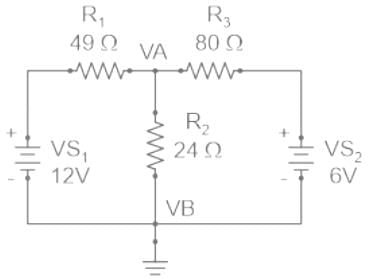
Find the value of V1 if the current through the 1 ohm resistor=0A.
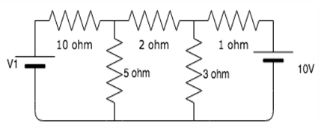
Calculate the mesh currents I1 and I2 flowing in the first and second meshes respectively.
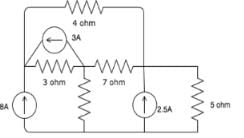
I1 is the current flowing in the first mesh. I2 is the current flowing in the second mesh and I3 is the current flowing in the top mesh. If all three currents are flowing in the clockwise direction, find the value of I1, I2 and I3.
Mesh analysis is generally used to determine _________
If there are 10 nodes in a circuit, how many equations do we get?
How many nodes are taken as reference nodes in nodal analysis?