All Courses
Get the App Signup / Login
Sign in Open App
Electrical Engineering (EE) Exam  >  Electrical Engineering (EE) Tests  >  Test: LTI System Frequency Characteristics - Electrical Engineering (EE) MCQ

Test: LTI System Frequency Characteristics - Electrical Engineering (EE) MCQ


Test Description

10 Questions MCQ Test - Test: LTI System Frequency Characteristics

Test: LTI System Frequency Characteristics for Electrical Engineering (EE) 2024 is part of Electrical Engineering (EE) preparation. The Test: LTI System Frequency Characteristics questions and answers have been prepared according to the Electrical Engineering (EE) exam syllabus.The Test: LTI System Frequency Characteristics MCQs are made for Electrical Engineering (EE) 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: LTI System Frequency Characteristics below.
Solutions of Test: LTI System Frequency Characteristics questions in English are available as part of our course for Electrical Engineering (EE) & Test: LTI System Frequency Characteristics solutions in Hindi for Electrical Engineering (EE) course. Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free. Attempt Test: LTI System Frequency Characteristics | 10 questions in 10 minutes | Mock test for Electrical Engineering (EE) preparation | Free important questions MCQ to study for Electrical Engineering (EE) Exam | Download free PDF with solutions
Test: LTI System Frequency Characteristics - Question 1
Save

 If x(n)=Aejωn is the input of an LTI system and h(n) is the response of the system, then what is the output y(n) of the system? 

Detailed Solution for Test: LTI System Frequency Characteristics - Question 1

Explanation: If x(n)= Aejωn is the input and h(n) is the response o the system, then we know that

Test: LTI System Frequency Characteristics - Question 2
Save

 If the system gives an output y(n)=H(ω)x(n) with x(n)= Aejωnas input signal, then x(n) is said to be Eigen function of the system.

Detailed Solution for Test: LTI System Frequency Characteristics - Question 2

Explanation: An Eigen function of a system is an input signal that produces an output that differs from the input by a constant multiplicative factor known as Eigen value of the system.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: LTI System Frequency Characteristics - Question 3
Save

What is the output sequence of the system with impulse response h(n)=(1/2)nu(n) when the input of the system is the complex exponential sequence x(n)=Aejnπ/2?

Detailed Solution for Test: LTI System Frequency Characteristics - Question 3

Explanation: First we evaluate the Fourier transform of the impulse response of the system h(n)

Test: LTI System Frequency Characteristics - Question 4
Save

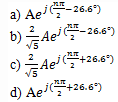
 If the Eigen function of an LTI system is x(n)= Aejnπ and the impulse response of the system is h(n)=(1/2)nu(n), then what is the Eigen value of the system? 
Detailed Solution for Test: LTI System Frequency Characteristics - Question 4

 

Explanation: First we evaluate the Fourier transform of the impulse response of the system h(n)

If the input signal is a complex exponential signal, then the input is known as Eigen function and H(ω) is called the Eigen value of the system. So, the Eigen value of the system mentioned above is 2/3.

Test: LTI System Frequency Characteristics - Question 5
Save

If h(n) is the real valued impulse response sequence of an LTI system, then what is the imaginary part of Fourier transform of the impulse response?
Detailed Solution for Test: LTI System Frequency Characteristics - Question 5

Explanation: From the definition of H(ω), we have

Test: LTI System Frequency Characteristics - Question 6
Save

 If h(n) is the real valued impulse response sequence of an LTI system, then what is the phase of H(ω) in terms of HR(ω) and HI(ω)?
Detailed Solution for Test: LTI System Frequency Characteristics - Question 6

Explanation: If h(n) is the real valued impulse response sequence of an LTI system, then H(ω) can be represented as HR(ω)+j HI(ω).
=>

Test: LTI System Frequency Characteristics - Question 7
Save

What is the magnitude of H(ω) for the three point moving average system whose output is given by y(n)=1/3[x(n+1)+x(n)+x(n-1)]?
Detailed Solution for Test: LTI System Frequency Characteristics - Question 7

Explanation: For a three point moving average system, we can define the output of the system as

Test: LTI System Frequency Characteristics - Question 8
Save

What is the magnitude of the frequency response of the system described by the difference equation y(n)=ay(n-1)+bx(n), 0<a<1?
Detailed Solution for Test: LTI System Frequency Characteristics - Question 8

Explanation: Given y(n)=ay(n-1)+bx(n)

Test: LTI System Frequency Characteristics - Question 9
Save

If an LTI system is described by the difference equation y(n)=ay(n-1)+bx(n), 0 < a < 1, then what is the parameter ‘b’ so that the maximum value of | H(ω)| is unity?
Detailed Solution for Test: LTI System Frequency Characteristics - Question 9

Explanation: We know that,

Since the parameter ‘a’ is positive, the denominator of | H(ω)| becomes minimum at ω=0. So, | H(ω)| attains its maximum value at ω=0. At this frequency we have,
(|b|)/(1-a) =1 =>b=±(1-a).

Test: LTI System Frequency Characteristics - Question 10
Save

 If an LTI system is described by the difference equation y(n)=ay(n-1)+bx(n), 0
Detailed Solution for Test: LTI System Frequency Characteristics - Question 10

Explanation: From the given difference equation, we obtain

Information about Test: LTI System Frequency Characteristics Page
In this test you can find the Exam questions for Test: LTI System Frequency Characteristics solved & explained in the simplest way possible. Besides giving Questions and answers for Test: LTI System Frequency Characteristics, EduRev gives you an ample number of Online tests for practice

Top Courses for Electrical Engineering (EE)

Download as PDF

Top Courses for Electrical Engineering (EE)

Important Questions for LTI System Frequency Characteristics

Find all the important questions for LTI System Frequency Characteristics at EduRev.Get fully prepared for LTI System Frequency Characteristics with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the LTI System Frequency Characteristics syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of LTI System Frequency Characteristics resources.

LTI System Frequency Characteristics MCQs with Answers

Prepare for the LTI System Frequency Characteristics within the Electrical Engineering (EE) exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for LTI System Frequency Characteristics

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace LTI System Frequency Characteristics with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup