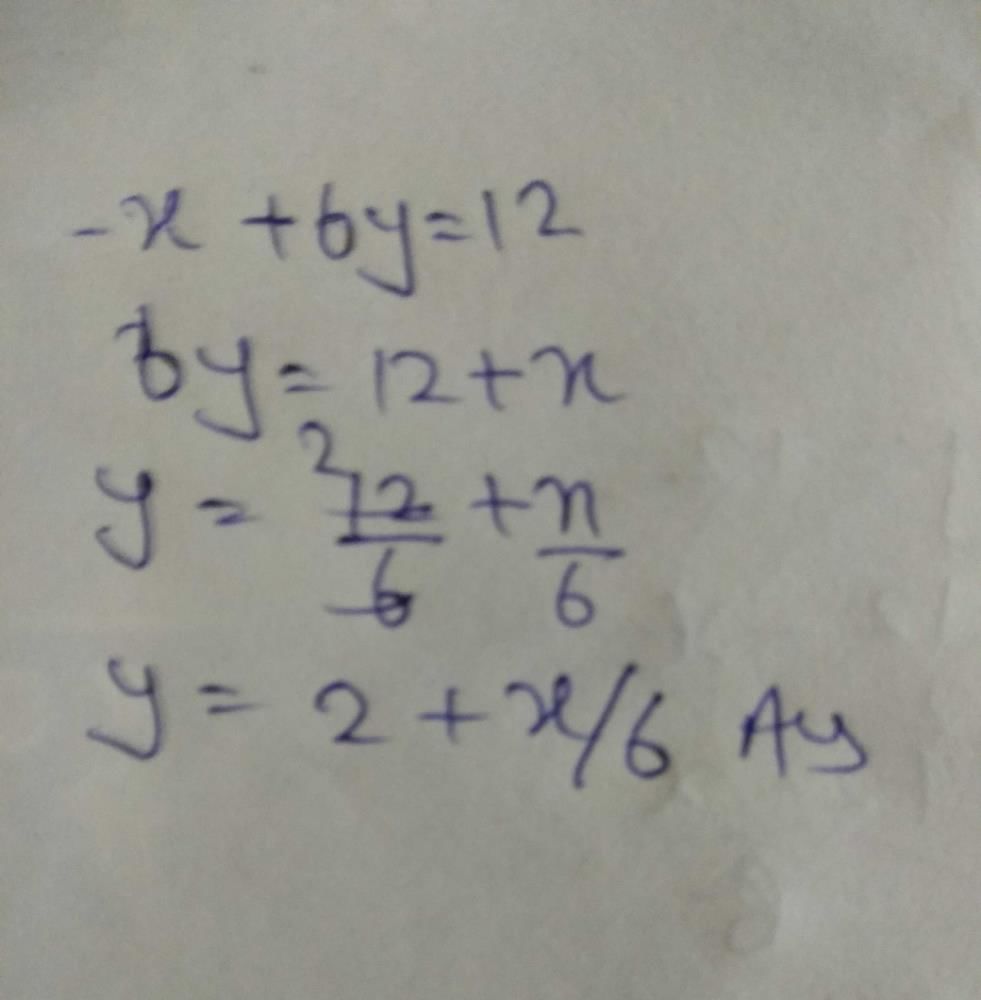All Courses
Get the App Signup / Login
Sign in Open App
Class 9 Exam  >  Class 9 Tests  >  Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ

Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ


Test Description

25 Questions MCQ Test - Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics

Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics for Class 9 2024 is part of Class 9 preparation. The Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics questions and answers have been prepared according to the Class 9 exam syllabus.The Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics MCQs are made for Class 9 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics below.
Solutions of Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics questions in English are available as part of our course for Class 9 & Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics solutions in Hindi for Class 9 course. Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free. Attempt Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics | 25 questions in 25 minutes | Mock test for Class 9 preparation | Free important questions MCQ to study for Class 9 Exam | Download free PDF with solutions
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 1
Save

Rozly can row downstream 20km in 2 hours, and the upstream 4km in 2 hours. What will be the speed of rowing in still water?       

Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 2
Save

If 2a – 3 = 5 and 3b + 1 = 2. Then 3b – 2a is :

1 Crore+ students have signed up on EduRev. Have you? Download the App
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 3
Save

The linear equation y = 2x + 3 cuts the y-axis at :

Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 4
Save

The equation 2x + 5y = 7 has a unique solution, if x, y are:
Detailed Solution for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 4
 In natural numbers, there is only one pair i.e., (1, 1) which satisfy the given equation but in positive real numbers, real numbers and rational numbers there are many pairs to satisfy the given linear equation.
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 5
Save

(2, 1) is a point which belong to the line :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 6
Save

One set of ordered pair which belong to a straight line represented by an equation y = 2x – 1 is :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 7
Save

Ordered pair that satisfy the in equation x + y + 1 < 0 is :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 8
Save

Which equation is the slope intercept form of –x + 6y = 12 :
Detailed Solution for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 8
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 9
Save

Which is an equation of the line with slope 2/3 that passes through the point (4, –1) ?
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 10
Save

 which equation fits the data in the table ?
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 11
Save

What is the slope of the line y = 2x – 3 ?
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 12
Save

Which of the following pairs of equations have the same solutions :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 13
Save

The option which is not a solution of the equation 2x + 3y = 6, is:
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 14
Save

ax + by + c = 0 does not represent equation of line if :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 15
Save

What will be the solution of these equations ax+by=a-b, bx-ay=a+b       
Detailed Solution for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 15
Ax+by=a-b
ax=a-b-by
x=a-b-by/a←
bx-ay=a+b
substituting
b(a-b-by/a)-ay=a+b
ab-b^2-b^2y/a-ay=a+b
ab-b^2-b^2y-a^2y/a=a+b
ab-b^2-(b^2+a^2)y=a^2+ab
-(b^2+a^2)y=a^2+ab-ab+b^2
(b^2+a^2)y=-(a^2+b^2)
y=-(a^2+b^2)/a^2+b^2
y=-1←
substituting value of y
x=a-b-b(-1)/a
x=a-b+b/a
x=a/a
x=1
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 16
Save

The equation y = 3x + 5n has :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 17
Save

The missing member 'x' in the ordered pair (x, – 8) if the second member of the pair is 4 more than the first member is :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 18
Save

Point of intersection of the lines x + y = 1 and x – y = 1 are :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 19
Save

Point of intersection of the lines x + y = 1 and 2x + 2y = 4 are :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 20
Save

The cost of a note book is twice the cost of a pen. If the cost of a note book is 'x' and that of a pen is 'y', then a linear equation in two variables to represent is :
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 21
Save

The graph of the line x = 4 passes through
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 22
Save

The graph of the line y = 3 passes through
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 23
Save

Which of the following is not a solution of 3x + 4y = 12?
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 24
Save

Any point on the x-axis is of the form
Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics - Question 25
Save

Any point on the y-axis is of the form
Information about Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics Page
In this test you can find the Exam questions for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics solved & explained in the simplest way possible. Besides giving Questions and answers for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 9

Download as PDF

Top Courses for Class 9

Important Questions for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics

Find all the important questions for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics at EduRev.Get fully prepared for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics resources.

Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics

Prepare for the Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics within the Class 9 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Linear Equation In Two Variables - Olympiad Level MCQ, Class 9 Mathematics with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup