Test: Pressure Distribution in a Fluid- 2 - Civil Engineering (CE) MCQ
15 Questions MCQ Test - Test: Pressure Distribution in a Fluid- 2
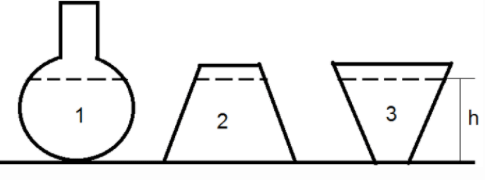
Three beakers 1, 2 and 3 of different shapes are kept on a horizontal table and filled with water up to a height h. If the pressure at the base of the beakers are P1, P2 and P3respectively, which one of the following will be the relation connecting the three?
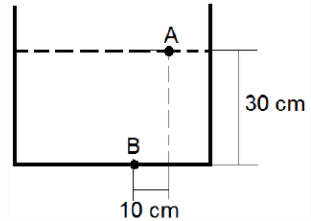
A beaker is filled with a liquid of specific gravity S = 1.2 as shown. What will be the pressure difference (in kN/m2) between the two points A and B, 30 cm below and 10 cm to the right of point A?
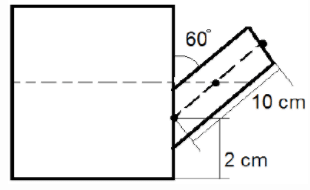
The arm of a teapot is 10 cm long and inclined at an angle of 60o to the vertical. The center of the arm base is 2 cm above the base of the beaker. Water is poured into the beaker such that half the arm is filled with it. What will be the pressure at the base of the beaker if the atmospheric pressure is 101.3 kPa?
A beaker of height 10 cm is half-filled with water (Sw = 1) and half-filled with oil (So = 0.08). At what distance (in cm) from the base will the pressure be half the pressure at the base of the beaker?
A beaker of height 30 cm is filled with water (Sw = 1) up to a height of 10 cm. Now oil (So = 0.8) is poured into the beaker till it is completely filled. At what distance (in cm) from the base will the pressure be one-third the pressure at the base of the beaker?
An oil tank of height 6 m is half-filled with oil and the air above it exerts a pressure of 200 kPa on the upper surface. The density of oil varies according to the given relation:
What will be the percentage error in the calculation of the pressure at the base of the tank if the density is taken to be a constant equal to 800?
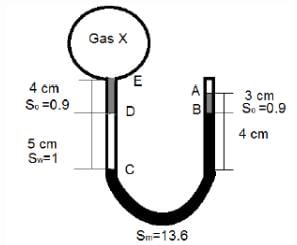
If a gas X be confined inside a bulb as shown, by what percent will the pressure of the gas be higher or lower than the atmospheric pressure? (Take the atmospheric pressure equal to 101.3 kPa)
A tank of height 3 cm is completely filled with water. Now two-third of the liquid is taken out and an equal amount of two other immiscible liquids of specific gravities 0.8 and 1.2 are poured into the tank. By what percent will the pressure at the base of the tank change?
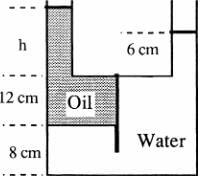
In Fig. P2.12 the tank contains water and immiscible oil at 20°C. What is h in centimeters if the density of the oil is 898 kg/m3?
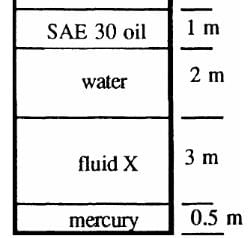
All fluids in Figure below are at 20°C. If atmospheric pressure = 101.33 kPa and the bottom pressure is 242 kPa absolute, what is the specific gravity of fluid X?
A liquid compressed in a cylinder has a volume of 0.04 m2 at 50 N/cm2 and a volume of 0.039 m3 at 150 N/cm2. The bulk modulus of elasticity of liquid i
The velocity distribution for flow over a flat plate is given by u = (y-y2) in which u is velocity in metres per second at a distance y metres above the plate. What is the shear stress value at y = 0.15 m? The dynamic viscosity of fluid is 8.0 poise.
For what height of the mercury column will the pressure inside the gas be 40 cm Hg vacuum?
In the space above the mercury column in a barometer tube, the gauge pressure of the vapour is
The pressure gauges G1 and G2 installed on the system show pressures of PG1 = 5.00 bar and PG2 =1.00 bar. The value of unknown pressure P is





















