|
|
Akanksha KapoorEduRev Mathematics |
|
|
Akanksha Kapoor
EduRev Mathematics
|
Content, tests & courses saved by you for accessing later. (visible to you only)
Discussed Questions
|
|
Akanksha Kapoor upvoted • 3 weeks ago |
For a partial differential equation, in a function φ (x, y) and two variables x, y, what is the form obtained after separation of variables is applied?- a)Φ (x, y) = X(x) + Y(y)
- b)Φ (x, y) = X(x) - Y(y)
- c)Φ (x, y) = X(x) / Y(y)
- d)Φ (x, y) = X(x)Y(y)
Correct answer is option 'D'. Can you explain this answer?
For a partial differential equation, in a function φ (x, y) and two variables x, y, what is the form obtained after separation of variables is applied?
a)
Φ (x, y) = X(x) + Y(y)
b)
Φ (x, y) = X(x) - Y(y)
c)
Φ (x, y) = X(x) / Y(y)
d)
Φ (x, y) = X(x)Y(y)

|
Veda Institute answered |
The method of separation of variables relies upon the assumption that a function of the form,
Φ (x, y) = X(x)Y(y)
will be a solution to a linear homogeneous partial differential equation in x and y. This is called a product solution and provided the boundary conditions are also linear and homogeneous this will also satisfy the boundary conditions.
Φ (x, y) = X(x)Y(y)
will be a solution to a linear homogeneous partial differential equation in x and y. This is called a product solution and provided the boundary conditions are also linear and homogeneous this will also satisfy the boundary conditions.
|
|
Akanksha Kapoor upvoted • Feb 24, 2025 |
The distance between the parallel planes 2x -2y + z + 3 = 0 and 4x -4y + 2z + 5 = 0 is- a)1/2
- b)1/3
- c)1/6
- d)none of the above
Correct answer is option 'C'. Can you explain this answer?
The distance between the parallel planes 2x -2y + z + 3 = 0 and 4x -4y + 2z + 5 = 0 is
a)
1/2
b)
1/3
c)
1/6
d)
none of the above

|
Veda Institute answered |
To find the distance between two parallel planes, we follow the method given below. Method:Find the perpendicular distance of each plane from the origin with proper sign (i.e. do not. lake the mod). Ther. their differeee is the required distance between two parallel planes. Let d. and d, be the distances of the planes
2x -2y + z + 3 =0 ...(i)
and 4x - 4y + 2z + 5 = 0 ...(ii)
from the origin. Then
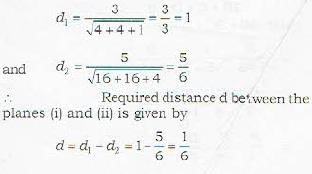
2x -2y + z + 3 =0 ...(i)
and 4x - 4y + 2z + 5 = 0 ...(ii)
from the origin. Then
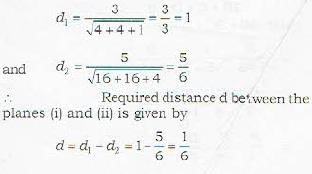
|
|
Akanksha Kapoor upvoted • Feb 09, 2025 |
If r > p > q, the number of different selections of p + q things taking r at a time, where p things are identical and q other things are identical, is- a)p + q - r
- b)q + q - r + 1
- c)r - p - q + 1
- d)non of these
Correct answer is option 'B'. Can you explain this answer?
If r > p > q, the number of different selections of p + q things taking r at a time, where p things are identical and q other things are identical, is
a)
p + q - r
b)
q + q - r + 1
c)
r - p - q + 1
d)
non of these

|
Veda Institute answered |
The number of selections of p things from p identical things and r - p things from q identical things = 1 x 1
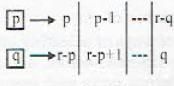
Similarly in all other cases,
∴ the total number of ways
= p - (r - q )+ 1 or q - (r - p) + 1
= p + q - r + l
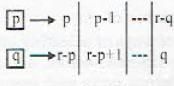
Similarly in all other cases,
∴ the total number of ways
= p - (r - q )+ 1 or q - (r - p) + 1
= p + q - r + l
|
|
Akanksha Kapoor upvoted • Feb 04, 2025 |
Let z be any non - zero complex number. Then arg(z) + arg(z¯) is equal to
- a)-π
- b)π
- c)0
- d)π/2
Correct answer is option 'C'. Can you explain this answer?
Let z be any non - zero complex number. Then arg(z) + arg(z¯) is equal to
a)
-π
b)
π
c)
0
d)
π/2

|
Veda Institute answered |
Let z = x+iy
zˉ = x−iy
arg(z) = xy,arg(zˉ) = −xy
arg(z) + arg(zˉ) = 0
|
|
Akanksha Kapoor upvoted • Jan 30, 2025 |
If 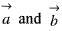 are to arbitrary vectors with magnitudes a and b respectively,
are to arbitrary vectors with magnitudes a and b respectively, 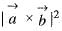 will be equal to
will be equal to- a)
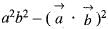
- b)
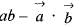
- c)

- d)
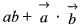
Correct answer is option 'A'. Can you explain this answer?
If 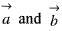 are to arbitrary vectors with magnitudes a and b respectively,
are to arbitrary vectors with magnitudes a and b respectively, 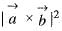 will be equal to
will be equal to
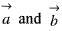 are to arbitrary vectors with magnitudes a and b respectively,
are to arbitrary vectors with magnitudes a and b respectively, 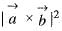 will be equal to
will be equal toa)
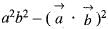
b)
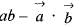
c)

d)
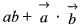

|
Veda Institute answered |
Cross checking from option (a),
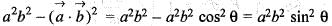
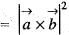
which is correct answer.
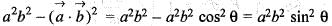
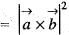
which is correct answer.
{(x1, x2, x3) belongs to R³ :x1+2x2+3x3=0} that is subspace?
|
|
Akanksha Kapoor answered • Dec 14, 2024 |
Subspace Definition
A subset W of a vector space V is a subspace if it satisfies three key properties:
- Contains the Zero Vector: The zero vector of V must be in W.
- Closed under Addition: If u and v are in W, then u + v must also be in W.
- Closed under Scalar Multiplication: If u is in W and c is a scalar, then cu must also be in W.
Verif... more
The set defined as {(x1, x2, x3) ∈ R³ : x1 + 2x2 + 3x3 = 0} can be examined for these properties.
1. Contains the Zero Vector
- The zero vector (0, 0, 0) satisfies the equation:
0 + 2(0) + 3(0) = 0.
- Therefore, the zero vector is included in this set.
2. Closed under Addition
- Let (x1, x2, x3) and (y1, y2, y3) be two vectors in the set such that:
x1 + 2x2 + 3x3 = 0 and y1 + 2y2 + 3y3 = 0.
- Adding these vectors gives:
(x1 + y1) + 2(x2 + y2) + 3(x3 + y3) = (x1 + 2x2 + 3x3) + (y1 + 2y2 + 3y3) = 0 + 0 = 0.
- Hence, the set is closed under addition.
3. Closed under Scalar Multiplication
- For any vector (x1, x2, x3) in the set and scalar c:
c(x1, x2, x3) = (cx1, cx2, cx3).
- We check:
cx1 + 2(cx2) + 3(cx3) = c(x1 + 2x2 + 3x3) = c(0) = 0.
- Thus, the set is closed under scalar multiplication.
Conclusion
Since all three properties are satisfied, the given set is indeed a subspace of R³.
A subset W of a vector space V is a subspace if it satisfies three key properties:
- Contains the Zero Vector: The zero vector of V must be in W.
- Closed under Addition: If u and v are in W, then u + v must also be in W.
- Closed under Scalar Multiplication: If u is in W and c is a scalar, then cu must also be in W.
Verif... more
The set defined as {(x1, x2, x3) ∈ R³ : x1 + 2x2 + 3x3 = 0} can be examined for these properties.
1. Contains the Zero Vector
- The zero vector (0, 0, 0) satisfies the equation:
0 + 2(0) + 3(0) = 0.
- Therefore, the zero vector is included in this set.
2. Closed under Addition
- Let (x1, x2, x3) and (y1, y2, y3) be two vectors in the set such that:
x1 + 2x2 + 3x3 = 0 and y1 + 2y2 + 3y3 = 0.
- Adding these vectors gives:
(x1 + y1) + 2(x2 + y2) + 3(x3 + y3) = (x1 + 2x2 + 3x3) + (y1 + 2y2 + 3y3) = 0 + 0 = 0.
- Hence, the set is closed under addition.
3. Closed under Scalar Multiplication
- For any vector (x1, x2, x3) in the set and scalar c:
c(x1, x2, x3) = (cx1, cx2, cx3).
- We check:
cx1 + 2(cx2) + 3(cx3) = c(x1 + 2x2 + 3x3) = c(0) = 0.
- Thus, the set is closed under scalar multiplication.
Conclusion
Since all three properties are satisfied, the given set is indeed a subspace of R³.
A homogeneous equation of nth degree represents- a)n straight lines passing through the origin
- b)At the most n straight lines passing through the origin
- c)At least one straight line passing through the origin
- d)n straight lines all of which either pass through origin or may not pass through the origin
Correct answer is option 'B'. Can you explain this answer?
A homogeneous equation of nth degree represents
a)
n straight lines passing through the origin
b)
At the most n straight lines passing through the origin
c)
At least one straight line passing through the origin
d)
n straight lines all of which either pass through origin or may not pass through the origin
|
|
Akanksha Kapoor answered • Sep 03, 2024 |
Understanding Homogeneous Equations of nth Degree
Homogeneous equations of the form \( f(x, y) = 0 \) where \( f \) is a polynomial of degree \( n \) have specific geometric interpretations, especially in the context of lines in the coordinate plane.
Characteristics of Homogeneous Equations:
- **Definition**: A homogeneous equation is one where every term is of t... more
Homogeneous equations of the form \( f(x, y) = 0 \) where \( f \) is a polynomial of degree \( n \) have specific geometric interpretations, especially in the context of lines in the coordinate plane.
Characteristics of Homogeneous Equations:
- **Definition**: A homogeneous equation is one where every term is of t... more
|
|
Akanksha Kapoor asked • Jun 20, 2024 |
The point (0,0) in the domain of f(x, y) = sin(xy) is a point of- a)Saddle
- b)Minima
- c)Maxima
- d)Constant
Correct answer is option 'A'. Can you explain this answer?
The point (0,0) in the domain of f(x, y) = sin(xy) is a point of
a)
Saddle
b)
Minima
c)
Maxima
d)
Constant

|
Veda Institute answered |
Differentiating fxx = -y2.sin(xy)
fyy = -x2.sin(xy)
fxy = -yx.sin(xy)
Observe that fxx. fyy – (fxy)2
Hence, it is a saddle point.
|
|
Akanksha Kapoor asked • Jun 12, 2024 |
The limit of sequence (an), (where an = 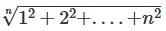 is ___________'Correct answer is '1'. Can you explain this answer?
is ___________'Correct answer is '1'. Can you explain this answer?
The limit of sequence (an), (where an = 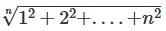 is ___________'
is ___________'
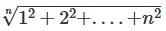 is ___________'
is ___________'

|
Veda Institute answered |
Note that
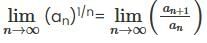
Here 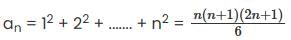
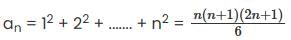
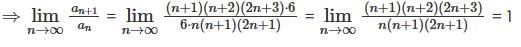
|
|
Akanksha Kapoor asked • Jun 05, 2024 |
Consider the statements:S1: Let G be an abelian group of order n if for every divisior m of n there exist a subgroup of G of order m, then G is cyclic.S2,: Let G be a group. If every proper sub group of G is cyclic then G is abelian.Which of the following is true.- a) S1, is true but S2 is not ture
- b) S2 is ture but S1 is not true
- c) Both are true
- d) Both are false
Correct answer is option 'D'. Can you explain this answer?
Consider the statements:
S1: Let G be an abelian group of order n if for every divisior m of n there exist a subgroup of G of order m, then G is cyclic.
S2,: Let G be a group. If every proper sub group of G is cyclic then G is abelian.
Which of the following is true.
a)
S1, is true but S2 is not ture
b)
S2 is ture but S1 is not true
c)
Both are true
d)
Both are false

|
Veda Institute answered |
S1: Take G=K4
Clearly G is an abelian group of order 4 and for every divisior of 4, G has a subgroup but G is not cyclic.
⇒ S1 is false
S2 : take G = Q8
Everyproper subgroup of G is cyclic but G is not abelian.
⇒ S2 is false
If G is a group of order 23 then find total no. of subgroups of group G.
Correct answer is '2'. Can you explain this answer?
If G is a group of order 23 then find total no. of subgroups of group G.
|
|
Akanksha Kapoor answered • Mar 05, 2024 |
Explanation:
Order of a group:
- The order of a group is the number of elements in the group.
- In this case, the order of group G is 23.
Subgroups of a group:
- A subgroup of a group is a subset of the group that is itself a group under the same operation.
- There are two trivial subgroups in any group: the group itself an... more
?
|
|
Akanksha Kapoor answered • Jan 19, 2024 |
CSIR NET Mathematics Test
The CSIR NET (Council of Scientific and Industrial Research National Eligibility Test) is a prestigious examination conducted for determining the eligibility of candidates for lectureship and Junior Research Fellowship (JRF) in various universities and institutes across India. The CSIR NET Mathematics paper covers a wide range of topics, including those relevant to IIT JAM and UGC NET exams.... more
Introduction:
The CSIR NET (Council of Scientific and Industrial Research National Eligibility Test) is a prestigious examination conducted for determining the eligibility of candidates for lectureship and Junior Research Fellowship (JRF) in various universities and institutes across India. The CSIR NET Mathematics paper covers a wide range of topics, including those relevant to IIT JAM and UGC NET exams.... more
The solution of y" + ay' + by = 0 where a and b are constants, approaches to zero as x → ∝ then- a)a > 0 ,b > 0
- b)a > 0 ,b < 0
- c)a < 0, b < 0
- d)a < 0, b > 0
Correct answer is option 'A'. Can you explain this answer?
The solution of y" + ay' + by = 0 where a and b are constants, approaches to zero as x → ∝ then
a)
a > 0 ,b > 0
b)
a > 0 ,b < 0
c)
a < 0, b < 0
d)
a < 0, b > 0
|
|
Akanksha Kapoor answered • Dec 17, 2023 |
Our problem is to analyze the situation and identify potential causes and solutions.
1. Identify the problem: The problem is that we are facing a high turnover rate in our company, which is resulting in decreased productivity and increased costs.
2. Analyze the causes: There could be several causes for the high turnover rate. Some possible causes include:
- Lack of... more
1. Identify the problem: The problem is that we are facing a high turnover rate in our company, which is resulting in decreased productivity and increased costs.
2. Analyze the causes: There could be several causes for the high turnover rate. Some possible causes include:
- Lack of... more
If g=z4×z2 and h=(2,0) then g/h is isomorphic to?
|
|
Akanksha Kapoor answered • Nov 26, 2023 |
Isomorphism in Group Theory
In mathematics, specifically in group theory, isomorphism is a concept that relates two groups. An isomorphism between two groups means that the two groups have the same structure and can be considered essentially the same. In this case, we are given two groups g and h, and we need to determine if g/h is isomorphic to any other group.
The... more
Let's start by understanding the given groups:
- Group g: g = Z4 × Z2
- Z4 is the cyclic group of integers modulo 4, denoted as {0, 1, 2, 3} with addition modulo 4.
- Z2 is the cyclic group of integers modulo 2, denoted as {0, 1} with addition modulo 2.
- Z4 × Z2 is the direct product of Z4 and Z2, which consists of ordered pairs (a, b) where a belongs to Z4 and b belongs to Z2. The group operation is defined component-wise, i.e., (a, b) + (c, d) = (a + c, b + d).
- Group h: h = (2, 0)
- h is a single element in the group, which represents an ordered pair (2, 0) in Z4 × Z2.
Isomorphism to Another Group
To determine if g/h is isomorphic to another group, we need to understand the quotient group g/h and its properties.
- Quotient Group g/h: g/h is the set of all left cosets of h in g. Each left coset is formed by taking an element g' from g and multiplying it on the left by the inverse of h. Mathematically, g/h = {g' * h | g' belongs to g}.
Since h = (2, 0), we can calculate the left cosets of h in g as follows:
- (0, 0) + h = {(0, 0) + (2, 0)} = {(2, 0)}
- (1, 0) + h = {(1, 0) + (2, 0)} = {(3, 0)}
- (2, 0) + h = {(2, 0) + (2, 0)} = {(0, 0)}
- (3, 0) + h = {(3, 0) + (2, 0)} = {(1, 0)}
Therefore, the quotient group g/h = {(2, 0), (3, 0), (0, 0), (1, 0)}.
Isomorphism Analysis
To determine if g/h is isomorphic to any other group, we need to consider the structure and properties of g/h.
- Size of g/h: The size of g/h is equal to the number of left cosets, which in this case is 4.
- Structure of g/h: The elements of g/h are (2, 0), (3, 0), (0, 0), (1, 0). We can observe that g/h is a cyclic group of order 4, as it contains all possible powers of (2, 0) in its
In mathematics, specifically in group theory, isomorphism is a concept that relates two groups. An isomorphism between two groups means that the two groups have the same structure and can be considered essentially the same. In this case, we are given two groups g and h, and we need to determine if g/h is isomorphic to any other group.
The... more
Let's start by understanding the given groups:
- Group g: g = Z4 × Z2
- Z4 is the cyclic group of integers modulo 4, denoted as {0, 1, 2, 3} with addition modulo 4.
- Z2 is the cyclic group of integers modulo 2, denoted as {0, 1} with addition modulo 2.
- Z4 × Z2 is the direct product of Z4 and Z2, which consists of ordered pairs (a, b) where a belongs to Z4 and b belongs to Z2. The group operation is defined component-wise, i.e., (a, b) + (c, d) = (a + c, b + d).
- Group h: h = (2, 0)
- h is a single element in the group, which represents an ordered pair (2, 0) in Z4 × Z2.
Isomorphism to Another Group
To determine if g/h is isomorphic to another group, we need to understand the quotient group g/h and its properties.
- Quotient Group g/h: g/h is the set of all left cosets of h in g. Each left coset is formed by taking an element g' from g and multiplying it on the left by the inverse of h. Mathematically, g/h = {g' * h | g' belongs to g}.
Since h = (2, 0), we can calculate the left cosets of h in g as follows:
- (0, 0) + h = {(0, 0) + (2, 0)} = {(2, 0)}
- (1, 0) + h = {(1, 0) + (2, 0)} = {(3, 0)}
- (2, 0) + h = {(2, 0) + (2, 0)} = {(0, 0)}
- (3, 0) + h = {(3, 0) + (2, 0)} = {(1, 0)}
Therefore, the quotient group g/h = {(2, 0), (3, 0), (0, 0), (1, 0)}.
Isomorphism Analysis
To determine if g/h is isomorphic to any other group, we need to consider the structure and properties of g/h.
- Size of g/h: The size of g/h is equal to the number of left cosets, which in this case is 4.
- Structure of g/h: The elements of g/h are (2, 0), (3, 0), (0, 0), (1, 0). We can observe that g/h is a cyclic group of order 4, as it contains all possible powers of (2, 0) in its
|
|
Akanksha Kapoor asked • Sep 30, 2023 |
Using the given data points tabulated below, a straight line passing through the origin is fitted using least squares method. The slope os the line is

- a)0.9
- b)1.0
- c)1.1
- d)1.5
Correct answer is option 'C'. Can you explain this answer?
Using the given data points tabulated below, a straight line passing through the origin is fitted using least squares method. The slope os the line is


a)
0.9
b)
1.0
c)
1.1
d)
1.5
|
|
Chirag Verma answered |
Suppose the line being, y = mx
Since, it has been fit by least square method, therefore
∑ y = μ ∑ x, and ∑ x y = μ ∑ x2
∴ m = 1.1
Since, it has been fit by least square method, therefore
∑ y = μ ∑ x, and ∑ x y = μ ∑ x2
∴ m = 1.1
IFT:R R² is a linear transformation given by Tix, y, z)=(x, y), Vix,y,ze R³ with respect to the standard basis of R³ and the basis [(1,0), (1,1)) of R². What is the matrix representation of T?
|
|
Akanksha Kapoor answered • Sep 28, 2023 |
Matrix Representation of T
To find the matrix representation of the linear transformation T with respect to the standard basis of R³ and the basis [(1,0), (1,1)) of R², we need to determine the images of the basis vectors (1,0,0), (0,1,0), and (0,0,1) under the transformation T.
Transformation of the Standard Basis
Let's first determine the images of ... more
To find the matrix representation of the linear transformation T with respect to the standard basis of R³ and the basis [(1,0), (1,1)) of R², we need to determine the images of the basis vectors (1,0,0), (0,1,0), and (0,0,1) under the transformation T.
Transformation of the Standard Basis
Let's first determine the images of ... more
What is the degree of the differential equation, x3 - 6x3 y3 + 2xy = 0?- a)3
- b)5
- c)8
- d)6
Correct answer is option 'D'. Can you explain this answer?
What is the degree of the differential equation, x3 - 6x3 y3 + 2xy = 0?
a)
3
b)
5
c)
8
d)
6
|
|
Akanksha Kapoor answered • Sep 28, 2023 |
Degree of a Differential Equation:
The degree of a differential equation is the highest power of the derivative present in the equation. To determine the degree, we need to identify the highest power of the derivative and simplify the equation if necessary.
Given Differential Equation:
The given differential equation is x^3 - 6x^3y^3 + 2xy = 0.
Step 1: S... more
The degree of a differential equation is the highest power of the derivative present in the equation. To determine the degree, we need to identify the highest power of the derivative and simplify the equation if necessary.
Given Differential Equation:
The given differential equation is x^3 - 6x^3y^3 + 2xy = 0.
Step 1: S... more
If nCn-1 = 36; nCr = 84 and nCr+1 = 126, then r is equal to:- a)1
- b)2
- c)3
- d)none
Correct answer is option 'C'. Can you explain this answer?
If nCn-1 = 36; nCr = 84 and nCr+1 = 126, then r is equal to:
a)
1
b)
2
c)
3
d)
none
|
|
Akanksha Kapoor answered • Sep 28, 2023 |
To find the value of r, we need to use the given equations: nCn-1 = 36, nCr = 84, and nCr1 = 126.
Using nCn-1 = 36:
The formula for combination is given by nCr = n! / (r! * (n-r)!), where n! represents the factorial of n.
Substituting n-1 in place of r, we get:
nCn-1 = n! / ((n-1)! * (n-(n-1))!) = n! / ((n-1)! * 1!)
Since (n-1)! is canceled out fro... more
Using nCn-1 = 36:
The formula for combination is given by nCr = n! / (r! * (n-r)!), where n! represents the factorial of n.
Substituting n-1 in place of r, we get:
nCn-1 = n! / ((n-1)! * (n-(n-1))!) = n! / ((n-1)! * 1!)
Since (n-1)! is canceled out fro... more
|
|
Akanksha Kapoor asked • Aug 17, 2023 |
Can I get the question papers for the IIT JAM Mathematics Exam without my signature on it?
|
|
Naina Rana answered |
Introduction:
The IIT JAM Mathematics Exam is a highly competitive entrance examination conducted by the Indian Institutes of Technology (IITs) for admission into their various postgraduate programs in mathematics. The question papers for the exam are essential study resources for candidates preparing for the test. However, obtaining these question papers without your signature on them... more
The IIT JAM Mathematics Exam is a highly competitive entrance examination conducted by the Indian Institutes of Technology (IITs) for admission into their various postgraduate programs in mathematics. The question papers for the exam are essential study resources for candidates preparing for the test. However, obtaining these question papers without your signature on them... more
|
|
Akanksha Kapoor asked • Aug 14, 2023 |
Can I get access to the admit card for the IIT JAM Mathematics Exam if my application is under scrutiny?
|
|
Oishi Bajaj answered |
Access to Admit Card for IIT JAM Mathematics Exam during Application Scrutiny
When applying for the IIT JAM Mathematics Exam, it is crucial to have access to the admit card as it serves as the entry ticket to the examination hall. However, if your application is under scrutiny, you may wonder whether you can still obtain your admit card. In this guide, we will provide you with a detailed explanation of the process and answer your query.... more
Introduction
When applying for the IIT JAM Mathematics Exam, it is crucial to have access to the admit card as it serves as the entry ticket to the examination hall. However, if your application is under scrutiny, you may wonder whether you can still obtain your admit card. In this guide, we will provide you with a detailed explanation of the process and answer your query.... more
|
|
Akanksha Kapoor asked • Aug 03, 2023 |
How can I use the marking scheme to analyze my performance in mock tests and practice papers for the IIT JAM Mathematics Exam?
|
|
Hrithik Choudhury answered |
How to Use the Marking Scheme to Analyze Performance in IIT JAM Mathematics Mock Tests and Practice Papers
Analyzing your performance in mock tests and practice papers is crucial for effective preparation for the IIT JAM Mathematics exam. One of the key tools for this analysis is the marking scheme provided with the question paper. Here's how you can use the marking scheme to eva... more
Analyzing your performance in mock tests and practice papers is crucial for effective preparation for the IIT JAM Mathematics exam. One of the key tools for this analysis is the marking scheme provided with the question paper. Here's how you can use the marking scheme to eva... more
|
|
Akanksha Kapoor asked • Aug 02, 2023 |
Can I get guidance from professors or teachers for clearing my doubts in the IIT JAM Mathematics syllabus?
|
|
Nakul Bajaj answered |
Getting Guidance from Professors or Teachers for Clearing Doubts in IIT JAM Mathematics Syllabus
1. Introduction:
Clearing doubts is an essential aspect of effective learning, especially for competitive exams like IIT JAM Mathematics. Seeking guidance from professors or teachers can greatly help in understanding complex concepts and solving difficult problems. Here ar... more
1. Introduction:
Clearing doubts is an essential aspect of effective learning, especially for competitive exams like IIT JAM Mathematics. Seeking guidance from professors or teachers can greatly help in understanding complex concepts and solving difficult problems. Here ar... more
Fetching relevant content for you






















