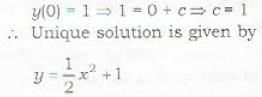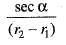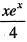|
|
Charvi VermaEduRev Mathematics |
|
|
Charvi Verma
EduRev Mathematics
|
Content, tests & courses saved by you for accessing later. (visible to you only)
Discussed Questions
What is the reason behind the non-existence of any real function which satisfies the differential equation, (y’)2 + 1 = 0?- a)Because for any real function, the left-hand side of the equation will be less than, or equal to one and thus cannot be zero
- b)Because for any real function, the left-hand side of the equation becomes zero
- c)Because for any real function, the left-hand side of the equation will be greater than, or equal to one and thus cannot be zero
- d)Because for any real function, the left-hand side of the equation becomes infinity
Correct answer is option 'C'. Can you explain this answer?
What is the reason behind the non-existence of any real function which satisfies the differential equation, (y’)2 + 1 = 0?
a)
Because for any real function, the left-hand side of the equation will be less than, or equal to one and thus cannot be zero
b)
Because for any real function, the left-hand side of the equation becomes zero
c)
Because for any real function, the left-hand side of the equation will be greater than, or equal to one and thus cannot be zero
d)
Because for any real function, the left-hand side of the equation becomes infinity
|
|
Charvi Verma answered • 2 weeks ago |
Understanding the Differential Equation
The differential equation given is (y')^2 + 1 = 0. Here, y' represents the derivative of the function y with respect to x.
Analyzing the Left-Hand Side
- The expression (y')^2 is the square of the derivative of y.
- Since squaring any real number (positive or negative) results in a non-negative value, (y')^2 is always greate... more
The differential equation given is (y')^2 + 1 = 0. Here, y' represents the derivative of the function y with respect to x.
Analyzing the Left-Hand Side
- The expression (y')^2 is the square of the derivative of y.
- Since squaring any real number (positive or negative) results in a non-negative value, (y')^2 is always greate... more
|
|
Charvi Verma upvoted • 3 weeks ago |
For a partial differential equation, in a function φ (x, y) and two variables x, y, what is the form obtained after separation of variables is applied?- a)Φ (x, y) = X(x) + Y(y)
- b)Φ (x, y) = X(x) - Y(y)
- c)Φ (x, y) = X(x) / Y(y)
- d)Φ (x, y) = X(x)Y(y)
Correct answer is option 'D'. Can you explain this answer?
For a partial differential equation, in a function φ (x, y) and two variables x, y, what is the form obtained after separation of variables is applied?
a)
Φ (x, y) = X(x) + Y(y)
b)
Φ (x, y) = X(x) - Y(y)
c)
Φ (x, y) = X(x) / Y(y)
d)
Φ (x, y) = X(x)Y(y)

|
Veda Institute answered |
The method of separation of variables relies upon the assumption that a function of the form,
Φ (x, y) = X(x)Y(y)
will be a solution to a linear homogeneous partial differential equation in x and y. This is called a product solution and provided the boundary conditions are also linear and homogeneous this will also satisfy the boundary conditions.
Φ (x, y) = X(x)Y(y)
will be a solution to a linear homogeneous partial differential equation in x and y. This is called a product solution and provided the boundary conditions are also linear and homogeneous this will also satisfy the boundary conditions.
|
|
Charvi Verma upvoted • Feb 09, 2025 |
Which of the following group is cyclic ?- a)S3
- b)Z5
- c)D4
- d)K4
Correct answer is option 'B'. Can you explain this answer?
Which of the following group is cyclic ?
a)
S3
b)
Z5
c)
D4
d)
K4

|
Veda Institute answered |
Concept used:
A group is cyclic iff there exists an element of order whose order is equal to the order of the group
Calculations:
o(S3) = 3!
contains 6 elements of the Symmetric group S(3), of degree 3, written in cycles are : {(1), (12), (13), (23), (123), (321)}.
o(1) = 1
o(12), o(23) and o(13) = 2
o(123), and o(321) = 3
no element having order equal to order of group
∴ option 1 is incorrect.
o(D4) = 8
D4 = {1, r, r2, r3 , s, sr, sr2, sr3}
o(s), o(sr), o(sr2), o(sr3) = 2
o(1) = 1, o(r) = 2 , o(r2) = 3, o(r3) = 4
no element having order equal to order of the group
∴ option 3 is incorrect.
o(K4) = 4
K4 = {e, a, b, ab}
o(e) = 1 , o(a) = 2, o(b) = 2, o(ab) = 2
No element having order equal to the order of group
∴ option 4 is incorrect.
o(Z5) = 5
Z5 = {0, 1, 2, 3, 4}
o(0) = 1 o(1) = 5, o(2) = 5 , o(3) = 5 , o(4) = 5
all elements having order = order of the group
all are the generator of the group.
∴ option 2 is correct.
If A = P {1, 2} where P denotes the power set, then which one of the following is correct?- a){1,2} ⊂ A
- b)1 ε A
- c)φ ∉ A
- d){1,2} ε A
Correct answer is option 'D'. Can you explain this answer?
If A = P {1, 2} where P denotes the power set, then which one of the following is correct?
a)
{1,2} ⊂ A
b)
1 ε A
c)
φ ∉ A
d)
{1,2} ε A
|
|
Charvi Verma answered • Nov 28, 2024 |
Understanding the Power Set
The power set P{1, 2} includes all possible subsets of the set {1, 2}. Let's first enumerate the elements of this power set:
- The subsets of {1, 2} are:
- The empty set: {}
- The set containing just the first element: {1}
- The set containing just the second element: {2}
- The set containing both elements: {1, 2}
Thus, the ... more
The power set P{1, 2} includes all possible subsets of the set {1, 2}. Let's first enumerate the elements of this power set:
- The subsets of {1, 2} are:
- The empty set: {}
- The set containing just the first element: {1}
- The set containing just the second element: {2}
- The set containing both elements: {1, 2}
Thus, the ... more
आज का विचार
"सफलता का असली मापदंड यह नहीं है कि आपने कितनी ऊँचाइयाँ हासिल कीं, बल्कि यह है कि जब ज़िंदगी ने आपको बार-बार गिराया, तब आपने कितनी बार अपने आप को समेटकर, हर टूटे हुए हिस्से को जोड़कर, फिर से खड़े होकर अपने स... more
|
|
Charvi Verma answered • Aug 11, 2024 |
Perseverance in the Face of Adversity
Success is not just about achieving great heights, but also about how we handle setbacks and challenges in life. It is easy to feel defeated when life throws obstacles in our path, but true success lies in our ability to rise every time we fall.
Strength in Resilience
When faced with failures and disappointments, it takes cou... more
Success is not just about achieving great heights, but also about how we handle setbacks and challenges in life. It is easy to feel defeated when life throws obstacles in our path, but true success lies in our ability to rise every time we fall.
Strength in Resilience
When faced with failures and disappointments, it takes cou... more
|
|
Charvi Verma asked • Jun 18, 2024 |
Convert the vector P to Cartesian coordinates where P = r ar + cosθ aφ.- a)
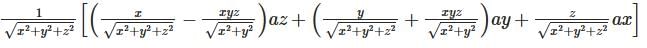
- b)
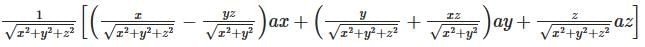
- c)

- d)
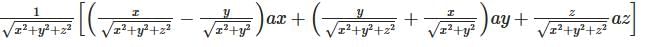
Correct answer is option 'B'. Can you explain this answer?
Convert the vector P to Cartesian coordinates where P = r ar + cosθ aφ.
a)
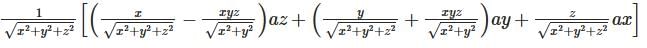
b)
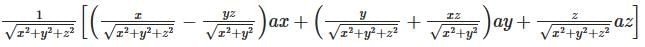
c)

d)
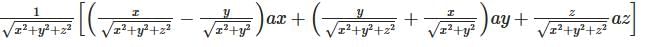

|
Veda Institute answered |
The formula to convert any vector from Spherical coordinates to Cartesian coordinates is given by
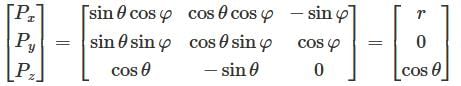
after substituting the values of the vector. Now, solving the matrix we get the answer
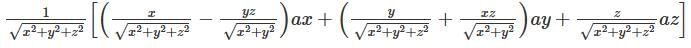
|
|
Charvi Verma asked • Jun 11, 2024 |
Let f: [a, b] → ℝ. Which of the following statement is/are true?- a)if f is continuous and injective, then f is monotone.
- b)if f is differentiable and f'(x) ≠0 for all x∈ (a.b), then f is injective.
- c)if f is differentiable and f'(a)<0< f'(b), then there is a c∈ (a,b) such that f'(c) = 0.
- d)if f is differentiable and f'(a)<d <f '(b), then there is a c∈ (a.b) such that f'(c) = d
Correct answer is option 'A,B,C,D'. Can you explain this answer?
Let f: [a, b] → ℝ. Which of the following statement is/are true?
a)
if f is continuous and injective, then f is monotone.
b)
if f is differentiable and f'(x) ≠0 for all x∈ (a.b), then f is injective.
c)
if f is differentiable and f'(a)<0< f'(b), then there is a c∈ (a,b) such that f'(c) = 0.
d)
if f is differentiable and f'(a)<d <f '(b), then there is a c∈ (a.b) such that f'(c) = d

|
Veda Institute answered |
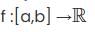
(c) & (d) follows from intermediate value theorem.
These are standard result and can be proved by contradiction.
All option are correct statement.
Suppose V is finite dimensional vector space over R .if W1 is subspace of V then prove that W1 not equal to V ,then span (V\W1)=V?
|
|
Charvi Verma answered • Apr 29, 2024 |
Proof:
Given:
V is a finite-dimensional vector space over R.
W1 is a subspace of V.
To Prove:
If W1 is not equal to V, then span(V\W1) = V.
Proof:
1. W1 is a Proper Subspace:
Since W1 is not equal to V, it implies that W1 is a proper subspace of V.
2. Dimension of V:
Since V is... more
Given:
V is a finite-dimensional vector space over R.
W1 is a subspace of V.
To Prove:
If W1 is not equal to V, then span(V\W1) = V.
Proof:
1. W1 is a Proper Subspace:
Since W1 is not equal to V, it implies that W1 is a proper subspace of V.
2. Dimension of V:
Since V is... more
(D² 1)³y=0, where D=d/dx?
|
|
Charvi Verma answered • Feb 23, 2024 |
Explanation:
The given differential equation is (D² 1)³y = 0, where D represents the differential operator d/dx.
Breaking down the equation:
- The term (D² 1) represents the second derivative of y with respect to x minus y.
- Raising this term to the power of 3 gives us ((d²/dx²) - y)³.
- Multiplying this by y gives us ((d²/dx²) - y)³y = 0.<... more
|
|
Charvi Verma asked • Feb 08, 2024 |
Let (-, -) be a symmetric bilinear form on ℝ2 such that there exist nonzero v, w ∈ ℝ2 such that (v, v) > 0 > (w, w) and (v, w) = 0. Let A be the 2 × 2 real symmetric matrix representing this bilinear form with respect to the standard basis. Which one of the following statements is true? - a)A2 = 0.
- b)rank A = 1
- c)rank A = 0.
- d)there exists u ∈ ℝ2, u ≠ 0 such that (u, u) = 0.
Correct answer is option 'D'. Can you explain this answer?
Let (-, -) be a symmetric bilinear form on ℝ2 such that there exist nonzero v, w ∈ ℝ2 such that (v, v) > 0 > (w, w) and (v, w) = 0. Let A be the 2 × 2 real symmetric matrix representing this bilinear form with respect to the standard basis. Which one of the following statements is true?
a)
A2 = 0.
b)
rank A = 1
c)
rank A = 0.
d)
there exists u ∈ ℝ2, u ≠ 0 such that (u, u) = 0.

|
Veda Institute answered |

Let (n, p) and λ be the parameters of binomial and poisson distributions respectively. Consider the statements
P. The mean of the binomial distribution is np
Q. The standard deviation of the binomial distribution is np (1 - p)
R. The mean of the poisson distribution is λ
S The variance of the poisson distribution is λ
Which of the following group of statements is correct?- a)P,R,S
- b)P,Q,S
- c)P,Q,R
- d)P,Q,R,S
Correct answer is option 'A'. Can you explain this answer?
Let (n, p) and λ be the parameters of binomial and poisson distributions respectively. Consider the statements
P. The mean of the binomial distribution is np
Q. The standard deviation of the binomial distribution is np (1 - p)
R. The mean of the poisson distribution is λ
S The variance of the poisson distribution is λ
Which of the following group of statements is correct?
P. The mean of the binomial distribution is np
Q. The standard deviation of the binomial distribution is np (1 - p)
R. The mean of the poisson distribution is λ
S The variance of the poisson distribution is λ
Which of the following group of statements is correct?
a)
P,R,S
b)
P,Q,S
c)
P,Q,R
d)
P,Q,R,S
|
|
Charvi Verma answered • Jan 12, 2024 |
R be two integers such that n > p > r > 0.
To prove that (n + p) choose r is equal to (n choose r) + (p choose r), we can use the definition of combinations.
According to the definition, (n choose r) represents the number of ways to choose r objects from a set of n objects, and (p choose r) represents the number of ways to choose r objects from a set of p objects.
... more
To prove that (n + p) choose r is equal to (n choose r) + (p choose r), we can use the definition of combinations.
According to the definition, (n choose r) represents the number of ways to choose r objects from a set of n objects, and (p choose r) represents the number of ways to choose r objects from a set of p objects.
If H be a subgroup of G, then H is normal in G, if- a)H is a subgroup of index 2 in G.
- b)H is a subgroup of index 3 in G.
- c)H is a subgroup of index 4 in G.
- d)H is a subgroup of index 5 in G.
Correct answer is option 'A'. Can you explain this answer?
If H be a subgroup of G, then H is normal in G, if
a)
H is a subgroup of index 2 in G.
b)
H is a subgroup of index 3 in G.
c)
H is a subgroup of index 4 in G.
d)
H is a subgroup of index 5 in G.
|
|
Charvi Verma answered • Nov 21, 2023 |
Explanation:
To show that H is normal in G, we need to show that for every element g in G, the conjugate of H by g, denoted by gHg^-1, is contained in H. In other words, for every h in H, we need to show that ghg^-1 is also in H.
Proof:
We will prove the given statement by showing that option A satisfies the condition for H being normal in G.
1. H i... more
Let G be a group and H be a subgroup of index 2 in G. This means that there are exactly two distinct left cosets of H in G, denoted by H and gH, where g is an element of G but not in H. Since there are only two cosets, they must be equal to each other, i.e., H = gH.
2. Conjugate of H by g:
Now, let's consider an arbitrary element h in H. We want to show that ghg^-1 is also in H for any g in G.
3. Case 1: g is in H:
If g is in H, then ghg^-1 is also in H because H is a subgroup and is closed under the group operation.
4. Case 2: g is not in H:
If g is not in H, then gH is the second left coset of H in G. Since H = gH, we have gH = H. Therefore, for any element h in H, we can write ghg^-1 = hg' for some g' in H.
5. Conclusion:
In both cases, we have shown that ghg^-1 is in H for any h in H. Therefore, H is normal in G.
6. Final Remarks:
We have proven that if H is a subgroup of index 2 in G, then H is normal in G. This result can be extended to other cases as well. However, options B, C, and D do not satisfy the condition for H being normal in G. Therefore, the correct answer is option A.
To show that H is normal in G, we need to show that for every element g in G, the conjugate of H by g, denoted by gHg^-1, is contained in H. In other words, for every h in H, we need to show that ghg^-1 is also in H.
Proof:
We will prove the given statement by showing that option A satisfies the condition for H being normal in G.
1. H i... more
Let G be a group and H be a subgroup of index 2 in G. This means that there are exactly two distinct left cosets of H in G, denoted by H and gH, where g is an element of G but not in H. Since there are only two cosets, they must be equal to each other, i.e., H = gH.
2. Conjugate of H by g:
Now, let's consider an arbitrary element h in H. We want to show that ghg^-1 is also in H for any g in G.
3. Case 1: g is in H:
If g is in H, then ghg^-1 is also in H because H is a subgroup and is closed under the group operation.
4. Case 2: g is not in H:
If g is not in H, then gH is the second left coset of H in G. Since H = gH, we have gH = H. Therefore, for any element h in H, we can write ghg^-1 = hg' for some g' in H.
5. Conclusion:
In both cases, we have shown that ghg^-1 is in H for any h in H. Therefore, H is normal in G.
6. Final Remarks:
We have proven that if H is a subgroup of index 2 in G, then H is normal in G. This result can be extended to other cases as well. However, options B, C, and D do not satisfy the condition for H being normal in G. Therefore, the correct answer is option A.
Let y(x) = 4(x) sinx + v(x) cos x be a solution of the differential equation, y”+y sec x, Then 4(x) is- a)In |cos x| + c
- b)-x+c
- c)X + c
- d)In|sec x| + c
Correct answer is option 'B'. Can you explain this answer?
Let y(x) = 4(x) sinx + v(x) cos x be a solution of the differential equation, y”+y sec x, Then 4(x) is
a)
In |cos x| + c
b)
-x+c
c)
X + c
d)
In|sec x| + c
|
|
Charvi Verma answered • Nov 21, 2023 |
To determine if y(x) = 4x sin(x) and v(x) = cos(x) is a solution of the differential equation, we need to substitute these functions into the equation and see if it holds true.
The differential equation is not provided, so we cannot determine if y(x) and v(x) are solutions without knowing the specific equation. Please provide the differential equation for further analysis.
The differential equation is not provided, so we cannot determine if y(x) and v(x) are solutions without knowing the specific equation. Please provide the differential equation for further analysis.
Factories the following by Euler's factorisation method 356957?
|
|
Charvi Verma answered • Nov 02, 2023 |
Factoring 356957 using Euler's factorisation method
Introduction
Euler's factorisation method is a technique used to factorize a given number into its prime factors. It is based on the concept of expressing a number as a product of its divisors.
Step 1: Prime factorisation of the given number
To factorize 356957 using Euler's factorisation metho... more
Introduction
Euler's factorisation method is a technique used to factorize a given number into its prime factors. It is based on the concept of expressing a number as a product of its divisors.
Step 1: Prime factorisation of the given number
To factorize 356957 using Euler's factorisation metho... more
Lim x approaches 64 (√x-8/3√x-4) Ans - 3?
|
|
Charvi Verma answered • Oct 18, 2023 |
Question: Lim x approaches 64 (√x-8/3√x-4) Ans - 3 Explain in details.
Solution:
To find the limit of the given expression as x approaches 64, we can substitute the value of x into the expression and simplify it.
Step 1: Substitute the value of x into the expression.
Let's substitute x = 64 into the expression (√x-8/3√x-4):
... more
Solution:
To find the limit of the given expression as x approaches 64, we can substitute the value of x into the expression and simplify it.
Step 1: Substitute the value of x into the expression.
Let's substitute x = 64 into the expression (√x-8/3√x-4):
... more
|
|
Charvi Verma asked • Sep 30, 2023 |
A single die is thrown twice. What is the sum is neither 8 nor 9?- a)1/9
- b)5/36
- c)1/4
- d)3/4
Correct answer is option 'D'. Can you explain this answer?
A single die is thrown twice. What is the sum is neither 8 nor 9?
a)
1/9
b)
5/36
c)
1/4
d)
3/4
|
|
Chirag Verma answered |
Here sample space = 36
Total No. of way in which sum is either 8 or 9 are (2,6), (3,5),(3,6),(4,4),(4,5),(5,3),(5,4),(6,2),(6,3)
So probability of getting sum 8 or 9 = 9/36 = 1/4
So the probability of not getting sum 8 or 9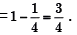
Total No. of way in which sum is either 8 or 9 are (2,6), (3,5),(3,6),(4,4),(4,5),(5,3),(5,4),(6,2),(6,3)
So probability of getting sum 8 or 9 = 9/36 = 1/4
So the probability of not getting sum 8 or 9
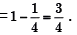
|
|
Charvi Verma asked • Aug 17, 2023 |
Can I get access to the question papers for the IIT JAM Mathematics Exam without my candidate ID mentioned on it?
|
|
Naina Rana answered |
Accessing IIT JAM Mathematics Exam Question Papers without Candidate ID:
Introduction:
Getting access to previous years' question papers can be extremely helpful in preparing for the IIT JAM Mathematics Exam. It allows candidates to understand the exam pattern, identify important topics, and practice solving questions within the given time limit. However, accessing th... more
Introduction:
Getting access to previous years' question papers can be extremely helpful in preparing for the IIT JAM Mathematics Exam. It allows candidates to understand the exam pattern, identify important topics, and practice solving questions within the given time limit. However, accessing th... more
|
|
Charvi Verma asked • Aug 14, 2023 |
Can you suggest some tips for mastering the concepts of vector calculus and multiple integrals for the IIT JAM Mathematics Paper?
|
|
Oishi Bajaj answered |
Mastering Vector Calculus and Multiple Integrals for IIT JAM Mathematics Paper
Introduction
Vector calculus and multiple integrals are important topics in mathematics that are often included in the IIT JAM Mathematics Paper. These concepts require a strong understanding of calculus and the ability to apply mathematical principles to solve complex problems. Here are so... more
Introduction
Vector calculus and multiple integrals are important topics in mathematics that are often included in the IIT JAM Mathematics Paper. These concepts require a strong understanding of calculus and the ability to apply mathematical principles to solve complex problems. Here are so... more
|
|
Charvi Verma asked • Aug 07, 2023 |
Can I get admission to an institute with a lower rank than the previous year's cutoff in the IIT JAM Mathematics Paper?
|
|
Radha Mehta answered |
Admission to an Institute with a Lower Rank than the Previous Year's Cutoff in IIT JAM Mathematics Paper
In order to secure admission to an institute with a lower rank than the previous year's cutoff in the IIT JAM Mathematics Paper, there are several factors that need to be considered. While a lower rank may reduce the chances of admission, it is not impossible to get admitted t... more
In order to secure admission to an institute with a lower rank than the previous year's cutoff in the IIT JAM Mathematics Paper, there are several factors that need to be considered. While a lower rank may reduce the chances of admission, it is not impossible to get admitted t... more
|
|
Charvi Verma asked • Aug 03, 2023 |
Is there any penalty for leaving a question unanswered in the IIT JAM Mathematics Exam?
|
|
Hrithik Choudhury answered |
Penalty for Leaving a Question Unanswered in the IIT JAM Mathematics Exam
Introduction:
The IIT JAM (Joint Admission Test for M.Sc.) is a national level entrance examination conducted by one of the Indian Institutes of Technology (IITs) for admission to various postgraduate programs, including Mathematics. It is important for candidates to understand the consequences ... more
Introduction:
The IIT JAM (Joint Admission Test for M.Sc.) is a national level entrance examination conducted by one of the Indian Institutes of Technology (IITs) for admission to various postgraduate programs, including Mathematics. It is important for candidates to understand the consequences ... more
Fetching relevant content for you