|
|
Ira MalhotraEduRev Mathematics |
|
Ira Malhotra
EduRev Mathematics
|
Content, tests & courses saved by you for accessing later. (visible to you only)
Discussed Questions
|
Ira Malhotra upvoted • 2 weeks ago |
What is the reason behind the non-existence of any real function which satisfies the differential equation, (y’)2 + 1 = 0?- a)Because for any real function, the left-hand side of the equation will be less than, or equal to one and thus cannot be zero
- b)Because for any real function, the left-hand side of the equation becomes zero
- c)Because for any real function, the left-hand side of the equation will be greater than, or equal to one and thus cannot be zero
- d)Because for any real function, the left-hand side of the equation becomes infinity
Correct answer is option 'C'. Can you explain this answer?
What is the reason behind the non-existence of any real function which satisfies the differential equation, (y’)2 + 1 = 0?
a)
Because for any real function, the left-hand side of the equation will be less than, or equal to one and thus cannot be zero
b)
Because for any real function, the left-hand side of the equation becomes zero
c)
Because for any real function, the left-hand side of the equation will be greater than, or equal to one and thus cannot be zero
d)
Because for any real function, the left-hand side of the equation becomes infinity
|
Veda Institute answered |
Given: (y’)2 + 1 = 0
Consider if y = 2x, then y’ = 2 and hence the left-hand side of the equation becomes 3 which is greater than 1. Therefore, the left-hand side of the equation will always be greater than, or equal to one and thus cannot be zero and hence the differential equation is not satisfied.
Consider if y = 2x, then y’ = 2 and hence the left-hand side of the equation becomes 3 which is greater than 1. Therefore, the left-hand side of the equation will always be greater than, or equal to one and thus cannot be zero and hence the differential equation is not satisfied.
|
|
Ira Malhotra upvoted • 4 weeks ago |
Let v1 = (1,0) v2 = (1,-1) and v3 = (0,1), then how many linear transformations T : R2 → R2 are there such that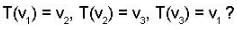 
Correct answer is '3'. Can you explain this answer?
Let v1 = (1,0) v2 = (1,-1) and v3 = (0,1), then how many linear transformations T : R2 → R2 are there such that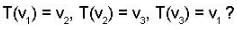
|
|
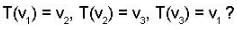
Veda Institute answered |
Since a linear transformation T : R2 → R2
defined as
⇒ T is cyclic linear transformation
where v1 = (1,0) v2 = (1,-1) v3 = (0,1)
here by {v1,v2,v3} we can get three sets of basis for R2
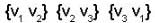
if we take {v1,v2} as the basis ad to determine linear transformation.
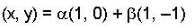
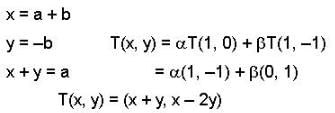
if we take {v2,v3} as the basis on determining linear transformation
defined as
⇒ T is cyclic linear transformation
where v1 = (1,0) v2 = (1,-1) v3 = (0,1)
here by {v1,v2,v3} we can get three sets of basis for R2
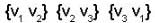
if we take {v1,v2} as the basis ad to determine linear transformation.
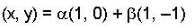
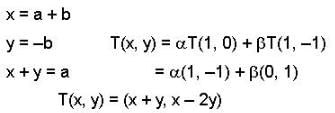
if we take {v2,v3} as the basis on determining linear transformation
|
|
Ira Malhotra upvoted • Feb 15, 2025 |
Let P4 (x) be a vector space of all polynomials with real coefficients of degree at most 4 emd V be a subspace of P4 (x), which spanned by the set {1-x, x+x2- X3, x3 + x2 + 1}.let T: V → P2 (x) be a L.T. defined by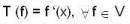
Then the nullity of T is ______ .
Correct answer is '1'. Can you explain this answer?
Let P4 (x) be a vector space of all polynomials with real coefficients of degree at most 4 emd V be a subspace of P4 (x), which spanned by the set {1-x, x+x2- X3, x3 + x2 + 1}.
let T: V → P2 (x) be a L.T. defined by
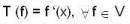
Then the nullity of T is ______ .
|
|
Veda Institute answered |
We know N (T ) = { f ∈ V / T ( F ) = 0}
|
|
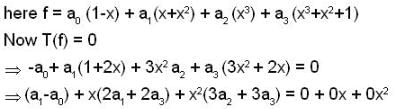
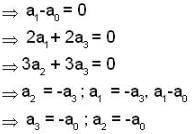
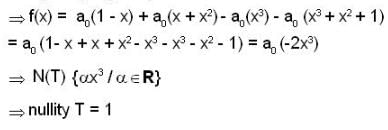
Ira Malhotra upvoted • Feb 07, 2025 |
What is the locus of a point for which y=b?- a)A plane parallel to ZX plane at a distance b from it
- b)A plane parallel to YX plane at a distance b from it
- c)A plane parallel to YZ plane at a distance b from it
- d)A line parallel to X axis at a distance b from it
Correct answer is option 'A'. Can you explain this answer?
What is the locus of a point for which y=b?
a)
A plane parallel to ZX plane at a distance b from it
b)
A plane parallel to YX plane at a distance b from it
c)
A plane parallel to YZ plane at a distance b from it
d)
A line parallel to X axis at a distance b from it
|
|
Veda Institute answered |
Note: We have
- Plane | | to xy piane at a distance c, z = c
- Plane; | | to t/x plane ai a distance a, x = a
- Plane | to xx plane at a distance b ,y = b
Remark:- In particular, the equations of YZ, ZX and XY planes are x = 0, y = 0 and z = 0 respectively.
|
|
Ira Malhotra upvoted • Feb 01, 2025 |
Which of the following transformations reduce the differential equation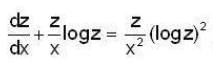 
into the form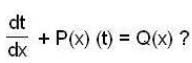 
- a)t = logz
- b)t= 1/log z
- c)t = ez
- d)t = (log z)2
Correct answer is option 'B'. Can you explain this answer?
Which of the following transformations reduce the differential equation 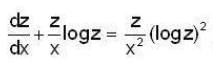into the form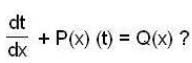
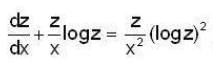into the form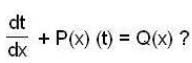 a)
t = logz
b)
t= 1/log z
c)
t = ez
d)
t = (log z)2
|
|
Veda Institute answered |
Given differential equation is
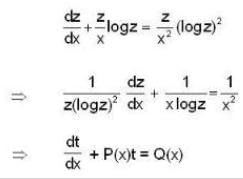
Here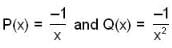 
which shows that the transformation t= 1/log z
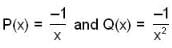which shows that the transformation t= 1/log z reduce the given differential equation into the form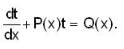 
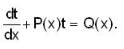
A fair coin is tossed twice. Let A be the event that at least one tail appears and B be the event that both head and tail appear. Then P[A/B], the probability of A given B, is- a)1/4
- b)1/2
- c)2/3
- d)1
Correct answer is option 'D'. Can you explain this answer?
A fair coin is tossed twice. Let A be the event that at least one tail appears and B be the event that both head and tail appear. Then P[A/B], the probability of A given B, is
a)
1/4
b)
1/2
c)
2/3
d)
1
|
|
Ira Malhotra answered • Nov 21, 2024 |
Understanding the Events
When a fair coin is tossed twice, the sample space (all possible outcomes) is:
- HH (two heads)
- HT (head and tail)
- TH (tail and head)
- TT (two tails)
Thus, the sample space contains 4 outcomes.
Defining Events A and B
- Event A: At least one tail appears. The outcomes that satisfy this are HT, TH, and TT.
- E... more
When a fair coin is tossed twice, the sample space (all possible outcomes) is:
- HH (two heads)
- HT (head and tail)
- TH (tail and head)
- TT (two tails)
Thus, the sample space contains 4 outcomes.
Defining Events A and B
- Event A: At least one tail appears. The outcomes that satisfy this are HT, TH, and TT.
- E... more
The general solution of y' - 2x-y is- a)2-x + 2-y = c
- b)2-x - 2-y = c
- c)2x + 2y = c
- d)2x - 2y = c
Correct answer is option 'D'. Can you explain this answer?
The general solution of y' - 2x-y is
a)
2-x + 2-y = c
b)
2-x - 2-y = c
c)
2x + 2y = c
d)
2x - 2y = c
|
|
Ira Malhotra answered • Aug 05, 2024 |
General Solution of the given equation:
- To find the general solution of the equation y - 2x - y = c, we first need to simplify it.
- Simplifying the equation gives us: -2x = c
- Rearranging the equation gives us the general solution: 2x = -c
Explanation of the correct answer:
- The correct answer is option 'D', which states that 2x - 2y = c.
- Th... more
- To find the general solution of the equation y - 2x - y = c, we first need to simplify it.
- Simplifying the equation gives us: -2x = c
- Rearranging the equation gives us the general solution: 2x = -c
Explanation of the correct answer:
- The correct answer is option 'D', which states that 2x - 2y = c.
- Th... more
|
|
Ira Malhotra asked • Jun 18, 2024 |
For the infinitely defined discontinuous function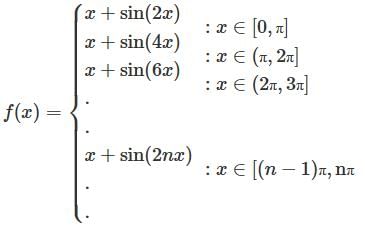
How many points 
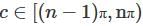such that- a) f ‘(c) = 1
- b)256
- c)512
- d)16
Correct answer is option 'A'. Can you explain this answer?
For the infinitely defined discontinuous function
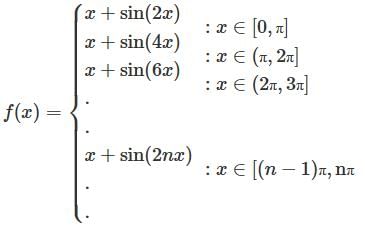
How many points 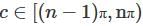such that
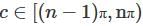such thata)
f ‘(c) = 1
b)
256
c)
512
d)
16
|
|
Veda Institute answered |
To find points such that f'(c) = 1
We need to check points on graph where slope remains the same ( 45 degrees)
In every interval of the form [(n – 1)π, nπ] we must have 2n – 1 points
Because sine curve there has frequency 2n and the graph is going to meet the graph y = x at 2n points.
Hence, in the interval [0, 16π] we have
= 1 + 3 + 5…….(16terms)
=(16)2 = 256.
|
|
Ira Malhotra asked • Jun 11, 2024 |
Choose the correct statements.- a)Every infinite and bounded set must have a limit point
- b)Any finite set cannot have a limit point
- c)Any infinite but unbounded set cannot have a limit point
- d)Every closed and bounded set has a limit point
Correct answer is option 'A,B'. Can you explain this answer?
Choose the correct statements.
a)
Every infinite and bounded set must have a limit point
b)
Any finite set cannot have a limit point
c)
Any infinite but unbounded set cannot have a limit point
d)
Every closed and bounded set has a limit point
|
|
Veda Institute answered |
Bolzano weierstrass theoremstate that, every bounded infinite set ofreal numbers has at least one limit point.
So (A) is true satetement.
Also if x be limit point of any set A, then by definition evely neighbourhood of x must contain infinitely many points of A, which is not possible if A is finite. So (B) is true statement.
(C) is wrong, as 
i.e. A have limit points.
i.e. A have limit points. (D) is wrong, as singleton set are always closed and bounded in ℝ. But do not have limit point.
Let F be a field and T be a linear operator on F2 defined by T(x1, x2) = (x1 + x2, x1). Then T-1(x1, x2) is- a)(x2, x1 - x2)
- b)(x1, x1 - x2)
- c)(x1 - x2, x2)
- d)(x1 - x2, x1)
Correct answer is option 'A'. Can you explain this answer?
Let F be a field and T be a linear operator on F2 defined by T(x1, x2) = (x1 + x2, x1). Then T-1(x1, x2) is
a)
(x2, x1 - x2)
b)
(x1, x1 - x2)
c)
(x1 - x2, x2)
d)
(x1 - x2, x1)
|
|
Ira Malhotra answered • May 28, 2024 |
Explanation:
Given linear operator:
T(x1, x2) = (x1 + x2, x1)
Finding the inverse of T:
To find the inverse of T, we need to solve for T-1(x1, x2) such that T(T-1(x1, x2)) = (x1, x2) and T-1(T(x1, x2)) = (x1, x2).
Solving for T-1(x1, x2):
Let T-1(x1, x2) = (a, b), then we have:
T(a, b) = (a + b, a) = (x1, x2)
... more
Given linear operator:
T(x1, x2) = (x1 + x2, x1)
Finding the inverse of T:
To find the inverse of T, we need to solve for T-1(x1, x2) such that T(T-1(x1, x2)) = (x1, x2) and T-1(T(x1, x2)) = (x1, x2).
Solving for T-1(x1, x2):
Let T-1(x1, x2) = (a, b), then we have:
T(a, b) = (a + b, a) = (x1, x2)
Given axa = b in a group G , where a,b ∈ G then x is equal to- a)a-1b
- b)a-1b-1
- c)a-1b-1b-1
- d)a-1ba-1
Correct answer is option 'D'. Can you explain this answer?
Given axa = b in a group G , where a,b ∈ G then x is equal to
a)
a-1b
b)
a-1b-1
c)
a-1b-1b-1
d)
a-1ba-1
|
|
Ira Malhotra answered • Feb 16, 2024 |
Are elements of the group G, we can conclude that there exists an element x in the group G such that ax = b.
This means that we can "cancel" the element a from both sides of the equation by multiplying both sides by a's inverse, denoted as a^(-1). So, we have:
a * x = b
a^(-1) * (a * x) = a^(-1) * b
(a^(-1) * a) * x = a^(-1) * b
e * x = a^(-1) * b
x = a^(-... more
This means that we can "cancel" the element a from both sides of the equation by multiplying both sides by a's inverse, denoted as a^(-1). So, we have:
a * x = b
a^(-1) * (a * x) = a^(-1) * b
(a^(-1) * a) * x = a^(-1) * b
e * x = a^(-1) * b
x = a^(-... more
|
|
Ira Malhotra asked • Feb 08, 2024 |
Let A and B two n × n matrices over real numbers. Let rank(M) and det(M) denote the rank and determinant of a matrix M, respectively. Consider the following statements.I. rank(AB) = rank(A) rank(B)II. det(AB) = det(A) det(B)III. rank(A + B) ≤ rank(A) + rank(B)IV. det(A + B) ≤ det(A) + det(B)Which of the above statements are TRUE?- a)I and II only
- b)I and IV only
- c)II and III only
- d)III and IV only
Correct answer is option 'C'. Can you explain this answer?
Let A and B two n × n matrices over real numbers. Let rank(M) and det(M) denote the rank and determinant of a matrix M, respectively. Consider the following statements.
I. rank(AB) = rank(A) rank(B)
II. det(AB) = det(A) det(B)
III. rank(A + B) ≤ rank(A) + rank(B)
IV. det(A + B) ≤ det(A) + det(B)
Which of the above statements are TRUE?
a)
I and II only
b)
I and IV only
c)
II and III only
d)
III and IV only
|
Arjun Mehta answered |
Understanding the Statements
In the context of two \( n \times n \) matrices \( A \) and \( B \), we need to evaluate the truth of the given statements.
Statement I: rank(AB) = rank(A) rank(B)
- This statement is generally false. The rank of the product \( AB \) can be less than or equal to the minimum of the ranks of \( A \) and \( B \). It does not hold that \(... more
In the context of two \( n \times n \) matrices \( A \) and \( B \), we need to evaluate the truth of the given statements.
Statement I: rank(AB) = rank(A) rank(B)
- This statement is generally false. The rank of the product \( AB \) can be less than or equal to the minimum of the ranks of \( A \) and \( B \). It does not hold that \(... more
Missiles are fired at a target. The probability of each missile hitting the targes is p : the hits are independent of one another. Each missile which hits the target brings it down with probability r. The missiles are fired until the target is brought down or the missile reserve is exhausted. the reserve consists of n missiles (n>2). Defining the event A as at least one missile will remain in reserve", the probability P(A) is:- a)1 (1-pr)n-1
- b)(1-pr)n-1
- c)(pr)n-1
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Missiles are fired at a target. The probability of each missile hitting the targes is p : the hits are independent of one another. Each missile which hits the target brings it down with probability r. The missiles are fired until the target is brought down or the missile reserve is exhausted. the reserve consists of n missiles (n>2). Defining the event A as at least one missile will remain in reserve", the probability P(A) is:
a)
1 (1-pr)n-1
b)
(1-pr)n-1
c)
(pr)n-1
d)
None of these
|
|
Ira Malhotra answered • Jan 10, 2024 |
The probability that the target is brought down after each missile is fired is r. The probability that the target is not brought down after each missile is fired is 1-r.
The probability that the target is brought down after exactly k missiles are fired is (p * r^k) * (1-r)^(k-1), where p is the probability of each missile hitting the target.
The probability that the target is... more
The probability that the target is brought down after exactly k missiles are fired is (p * r^k) * (1-r)^(k-1), where p is the probability of each missile hitting the target.
The probability that the target is... more
Let A be a 4 x 4 matrix with real entries such that - 1, 1, 2, - 2 are its eigen values. If B = A4 - 5A2 + 5I, where I denotes the 4 x 4 identity matrix, then which of the following statements are correct?- a)det(A + B) = 0
- b)det (B) = 1
- c)trace of A - B is 0
- d)trace of A + B is 4
Correct answer is option 'C'. Can you explain this answer?
Let A be a 4 x 4 matrix with real entries such that - 1, 1, 2, - 2 are its eigen values. If B = A4 - 5A2 + 5I, where I denotes the 4 x 4 identity matrix, then which of the following statements are correct?
a)
det(A + B) = 0
b)
det (B) = 1
c)
trace of A - B is 0
d)
trace of A + B is 4
|
|
Ira Malhotra answered • Nov 22, 2023 |
Given information:
- A is a 4x4 matrix with real entries.
- The eigenvalues of A are -1, 1, 2, -2.
- B = A^4 - 5A^2 + 5I, where I is the 4x4 identity matrix.
To find the correct statements, let's analyze each option:
a) det(A B) = 0
To determine det(A B), we need to compute the determinant of the matrix [A B]. Since B is defined in terms of A, let's substi... more
- A is a 4x4 matrix with real entries.
- The eigenvalues of A are -1, 1, 2, -2.
- B = A^4 - 5A^2 + 5I, where I is the 4x4 identity matrix.
To find the correct statements, let's analyze each option:
a) det(A B) = 0
To determine det(A B), we need to compute the determinant of the matrix [A B]. Since B is defined in terms of A, let's substi... more
A is any n x n matrix with entries equal to 1 then- a)multiplicity of 0 is n - 1
- b)multiplicity of 0 is 1
- c)multiplicity of 0 is n
- d)multiplicity of 0 is
Correct answer is option 'A'. Can you explain this answer?
A is any n x n matrix with entries equal to 1 then
a)
multiplicity of 0 is n - 1
b)
multiplicity of 0 is 1
c)
multiplicity of 0 is n
d)
multiplicity of 0 is
|
|
Ira Malhotra answered • Nov 22, 2023 |
Explanation:
To find the multiplicity of the eigenvalue 0 in the given matrix A, we need to find the number of linearly independent eigenvectors corresponding to the eigenvalue 0.
1. Eigenvectors and eigenvalues:
An eigenvector of a matrix A is a non-zero vector v such that Av = λv, where λ is a scalar called the eigenvalue corresponding to v.
<... more
To find the multiplicity of the eigenvalue 0 in the given matrix A, we need to find the number of linearly independent eigenvectors corresponding to the eigenvalue 0.
1. Eigenvectors and eigenvalues:
An eigenvector of a matrix A is a non-zero vector v such that Av = λv, where λ is a scalar called the eigenvalue corresponding to v.
<... more
Using the transformation u = w/y in the p. d. e xux = u + yuy the transformed equation has solution of the form w =- a)f(x/y)
- b)f( x + y)
- c)f ( x - y )
- d)f(xy)
Correct answer is option 'B'. Can you explain this answer?
Using the transformation u = w/y in the p. d. e xux = u + yuy the transformed equation has solution of the form w =
a)
f(x/y)
b)
f( x + y)
c)
f ( x - y )
d)
f(xy)
|
|
Ira Malhotra answered • Oct 19, 2023 |
To find the solution of the given partial differential equation (PDE), we need to use the transformation u = w/y. Let's go step by step to understand the process.
1. Transformation:
- Given PDE: xux = u * yuy
- Let's substitute u = w/y in the PDE:
x * (w/y) * x = (w/y) * y * y * (dw/dy)
- Simplifying the equation:
x^2 * (dw/dy) = w * y
... more
1. Transformation:
- Given PDE: xux = u * yuy
- Let's substitute u = w/y in the PDE:
x * (w/y) * x = (w/y) * y * y * (dw/dy)
- Simplifying the equation:
x^2 * (dw/dy) = w * y
The probability that a radar will detect an object in one cycle is p. The probability that it will be detected in n cycles is- a)1-pn
- b)1-(1-p)n
- c)pn
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The probability that a radar will detect an object in one cycle is p. The probability that it will be detected in n cycles is
a)
1-pn
b)
1-(1-p)n
c)
pn
d)
None of these
|
|
Ira Malhotra answered • Oct 19, 2023 |
Explanation:
To understand why the correct answer is option B, let's break down the problem step by step.
Probability of not detecting an object in one cycle:
The probability of not detecting an object in one cycle is 1-p. This is because the probability of detecting an object in one cycle is p, so the probability of not detecting it is 1-p.
P... more
If the probability of not detecting an object in one cycle is 1-p, then the probability of not detecting it in n cycles is (1-p)^n. This is because each cycle is an independent event, and the probability of not detecting the object in each cycle is the same (1-p).
Probability of detecting an object in n cycles:
The probability of detecting an object in n cycles is 1 minus the probability of not detecting it in n cycles. So, the probability of detecting an object in n cycles is 1 - (1-p)^n.
Therefore, the correct answer is option B: 1 - (1-p)^n. This formula gives us the probability of detecting an object in n cycles, taking into account the probability of not detecting it in each cycle.
To understand why the correct answer is option B, let's break down the problem step by step.
Probability of not detecting an object in one cycle:
The probability of not detecting an object in one cycle is 1-p. This is because the probability of detecting an object in one cycle is p, so the probability of not detecting it is 1-p.
P... more
If the probability of not detecting an object in one cycle is 1-p, then the probability of not detecting it in n cycles is (1-p)^n. This is because each cycle is an independent event, and the probability of not detecting the object in each cycle is the same (1-p).
Probability of detecting an object in n cycles:
The probability of detecting an object in n cycles is 1 minus the probability of not detecting it in n cycles. So, the probability of detecting an object in n cycles is 1 - (1-p)^n.
Therefore, the correct answer is option B: 1 - (1-p)^n. This formula gives us the probability of detecting an object in n cycles, taking into account the probability of not detecting it in each cycle.
Let g be a non abelian group of order 729 then the no. of conjugate class is?
|
|
Ira Malhotra answered • Oct 09, 2023 |
Explanation:
To find the number of conjugate classes in a non-abelian group of order 729, we need to understand the concept of conjugacy in group theory.
Conjugacy in Group Theory:
In group theory, two elements a and b of a group G are said to be conjugate if there exists an element g in G such that b = gag⁻¹. In other words, two elements are conjugate if they are related by a change of basis.... more
|
|
Ira Malhotra asked • Aug 17, 2023 |
How can I use the marking weightage to set realistic goals and target scores for the IIT JAM Mathematics Exam?
|
Naina Rana answered |
Setting Realistic Goals and Target Scores for the IIT JAM Mathematics Exam using Marking Weightage
The marking weightage refers to the allocation of marks to different topics or sections of the IIT JAM Mathematics exam. It gives an indication of the importance of each topic and helps in determining the areas that require more focus and preparation. By analyzing the marking weightage, you can set realistic goals and target scores for the exam.... more
Understanding Marking Weightage
The marking weightage refers to the allocation of marks to different topics or sections of the IIT JAM Mathematics exam. It gives an indication of the importance of each topic and helps in determining the areas that require more focus and preparation. By analyzing the marking weightage, you can set realistic goals and target scores for the exam.... more
|
|
Ira Malhotra asked • Aug 17, 2023 |
Can I get access to the question papers for the IIT JAM Mathematics Exam without my application number mentioned on it?
|
|
Naina Rana answered |
Accessing IIT JAM Mathematics Exam Question Papers without Application Number
The IIT JAM (Joint Admission Test for M.Sc.) is a prestigious entrance examination for candidates seeking admission to various postgraduate programs at the Indian Institutes of Technology (IITs). To access the question papers for the IIT JAM Mathematics Exam, it is generally required to provide your application number. However, there are alternative ways to obtain these question papers even if you do not have your application number handy.... more
Introduction
The IIT JAM (Joint Admission Test for M.Sc.) is a prestigious entrance examination for candidates seeking admission to various postgraduate programs at the Indian Institutes of Technology (IITs). To access the question papers for the IIT JAM Mathematics Exam, it is generally required to provide your application number. However, there are alternative ways to obtain these question papers even if you do not have your application number handy.... more
|
|
Ira Malhotra asked • Aug 14, 2023 |
Are there any specific steps I need to follow to download the admit card for the IIT JAM Mathematics Paper?
|
Oishi Bajaj answered |
How to Download IIT JAM Mathematics Admit Card
Introduction:
The IIT JAM (Joint Admission Test for M.Sc.) is a national level entrance exam conducted by the Indian Institutes of Technology (IITs) for admission to various postgraduate programs. To appear for the IIT JAM Mathematics paper, candidates must download the admit card, which serves as an entry ticket to the e... more
Introduction:
The IIT JAM (Joint Admission Test for M.Sc.) is a national level entrance exam conducted by the Indian Institutes of Technology (IITs) for admission to various postgraduate programs. To appear for the IIT JAM Mathematics paper, candidates must download the admit card, which serves as an entry ticket to the e... more
|
|
Ira Malhotra asked • Aug 07, 2023 |
Are there any minimum qualifying marks required in each section of the IIT JAM Mathematics Paper to be considered for admission?
|
Radha Mehta answered |
Minimum Qualifying Marks in IIT JAM Mathematics Paper
To be considered for admission to the Mathematics program through the IIT JAM exam, candidates need to secure minimum qualifying marks in each section of the paper. The IIT JAM Mathematics Paper consists of three sections: Section A, Section B, and Section C. Let's discuss the minimum qualifying marks required in each section ... more
To be considered for admission to the Mathematics program through the IIT JAM exam, candidates need to secure minimum qualifying marks in each section of the paper. The IIT JAM Mathematics Paper consists of three sections: Section A, Section B, and Section C. Let's discuss the minimum qualifying marks required in each section ... more
Fetching relevant content for you
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup