|
|
Pijush DeIf you don't have any shadows, you're not standing in the light. |
|
|
Pijush De
EduRev UGC NET
|
Content, tests & courses saved by you for accessing later. (visible to you only)
Top Scoring Tests by Pijush
Test: Matrix | 55/60 |
Test: Food-Where Does It Come From | 35/40 |
Test: Linear Algebra | 17/20 |
AIIMS General Knowledge Mock Test - 2 | 7/10 |
Differential Equations - 12 | 51/80 |
RS Aggarwal Test: Real Numbers - 1 | 25/40 |
Definite Integrals MCQ - 1 | 6/10 |
Test: Vector Analysis - 1 | 6/10 |
Test: Real Analysis - 3 | 42/80 |
Test: Real Analysis- 1 | 41/80 |
Discussed Questions
Let T be linear transformation on 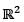 into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
- a)(a, 2b)
- b)(2a, b)
- c)(a - b, 2a)
- d)(a - b, 2b)
Correct answer is option 'C'. Can you explain this answer?
Let T be linear transformation on 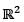 into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
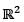 into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal to
into itself such that T(1,0) = (1,2) and T (1, 1) = (0, 2) .Then T(a, b) is equal toa)
(a, 2b)
b)
(2a, b)
c)
(a - b, 2a)
d)
(a - b, 2b)

|
Pijush De answered • Dec 09, 2021 |
As {(1,0),(1,1)} form a basis for R^2 so, (a,b) can be written as Linear combination of (1,0) &(1,1).
(a,b) = (a-b)(1,0) + b(1,1)
So, T(a,b) = T(b(1,1) + (a-b)(1,0))
= b T(1,1) + (a-b) T(1,0)
= b (0,2) + (a-b) (1,2)
= (a-b, 2a) [Option C]
(a,b) = (a-b)(1,0) + b(1,1)
So, T(a,b) = T(b(1,1) + (a-b)(1,0))
= b T(1,1) + (a-b) T(1,0)
= b (0,2) + (a-b) (1,2)
= (a-b, 2a) [Option C]
Let ∑an be a convergent series of positive terms and let ∑bn be a divergent series of positive terms. Then,
... more
Let ∑an be a convergent series of positive terms and let ∑bn be a divergent series of positive terms. Then,

|
Pijush De answered • Dec 09, 2021 |
To discard options A), B), C) take bn = 1/n .
Option D) is correct because for the series to be convergent, it is needed that the sequence converges, and converges to 0.(But the reverse is false)
Composite number n is- a)a prime number and n > 1
- b)non-prime number n < 1
- c)non-prime number and n > 1
- d)a prime number and n < 1
Correct answer is option 'C'. Can you explain this answer?
Composite number n is
a)
a prime number and n > 1
b)
non-prime number n < 1
c)
non-prime number and n > 1
d)
a prime number and n < 1

|
Pijush De answered • Feb 27, 2021 |
Composite numbers can be defined as natural numbers that have more than two factors. In other words, a number which is divisible by a number other than 1 and the number itself, is called a composite number. So composite number never be a prime and also not equal to 1. So the correct answer is option 'C'.
The number of divisiors of 9600 including 1 and 9600 is- a)60
- b)58
- c)48
- d)46
Correct answer is option 'C'. Can you explain this answer?
The number of divisiors of 9600 including 1 and 9600 is
a)
60
b)
58
c)
48
d)
46

|
Pijush De answered • Feb 27, 2021 |
For this we apply tau function or the number of divisors function, denoted by τ is defined by setting τ(n) equal to the number of positive divisors of n.
Here n = 9600 = 2^7×3×5^2 and τ(9600) = (7+1)×(1+1)×(2+1) = 48 (option C).
Here n = 9600 = 2^7×3×5^2 and τ(9600) = (7+1)×(1+1)×(2+1) = 48 (option C).
The number of positive divisiors of 50,000 is- a)20
- b)30
- c)40
- d)50
Correct answer is option 'B'. Can you explain this answer?
The number of positive divisiors of 50,000 is
a)
20
b)
30
c)
40
d)
50

|
Pijush De answered • Feb 27, 2021 |
For this we apply tau function or the number of divisors function, denoted by τ is defined by setting τ(n) equal to the number of positive divisors of n.
Here n = 50000 = 5^5×2^4 and τ(50000) = (5+1)×(4+1) = 30 (option B).
Here n = 50000 = 5^5×2^4 and τ(50000) = (5+1)×(4+1) = 30 (option B).
Let <an> be a sequence of real numbers such that lim in f (an) = 0 and lim sup (an ) = T. Then,- a)all the terms should lie between 0 and 1.
- b)there must be infinitely many terms between 0 and 1.
- c)there are only finitely many terms between -1 and 2.
- d)there are only finitely many terms outside of [0, 1].
Correct answer is option 'B'. Can you explain this answer?
Let <an> be a sequence of real numbers such that lim in f (an) = 0 and lim sup (an ) = T. Then,
a)
all the terms should lie between 0 and 1.
b)
there must be infinitely many terms between 0 and 1.
c)
there are only finitely many terms between -1 and 2.
d)
there are only finitely many terms outside of [0, 1].

|
Pijush De answered • Feb 27, 2021 |

The following table defines a cyclic group

its generators are- a)A,B
- b)D, B
- c)C, D
- d)D, A
Correct answer is option 'D'. Can you explain this answer?
The following table defines a cyclic group

its generators are

its generators are
a)
A,B
b)
D, B
c)
C, D
d)
D, A

|
Pijush De answered • Feb 27, 2021 |
From 2nd row & 2nd column of the above table we see that B is the identity element. Now the number of generators of a cyclic group can be found using Euler's phi function.
Here φ(4) = φ(2^2) = (2^2) - 2 = 2 i.e. the group has 2 generators. Now C^2 = B = Identity element. So order of C = 2 ≠ 4 ⇒C isn't a generator for a group of order 4 & also B is the identity element. Therefore the two generator... more
The number of generators in cyclic group of order 10 are- a)3
- b)1
- c)2
- d)4
Correct answer is option 'D'. Can you explain this answer?
The number of generators in cyclic group of order 10 are
a)
3
b)
1
c)
2
d)
4

|
Pijush De answered • Feb 27, 2021 |
Use Euler's phi function as follows :
Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n and denoted by Greek letter phi as φ(n). The number of generators of a cyclic group can be found using Euler's phi function.
So here φ(10) = φ(5)×φ(2) [as 5 & 2 are relatively prime]. = (5 -1) × 1 = 4.
Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n and denoted by Greek letter phi as φ(n). The number of generators of a cyclic group can be found using Euler's phi function.
So here φ(10) = φ(5)×φ(2) [as 5 & 2 are relatively prime]. = (5 -1) × 1 = 4.
Number of elements of the cyclic group of order 6 can be used as generators of the group are- a)= 3
- b)= 5
- c)= 2
- d)4
Correct answer is option 'C'. Can you explain this answer?
Number of elements of the cyclic group of order 6 can be used as generators of the group are
a)
= 3
b)
= 5
c)
= 2
d)
4

|
Pijush De answered • Feb 27, 2021 |
Use Euler's phi function as follows :
Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n and denoted by Greek letter phi as φ(n). The number of generators of a cyclic group can be found using Euler's phi function.
So here φ(6) = φ(3)×φ(2) [as 3 & 2 are relatively prime]. = 2.
Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n and denoted by Greek letter phi as φ(n). The number of generators of a cyclic group can be found using Euler's phi function.
So here φ(6) = φ(3)×φ(2) [as 3 & 2 are relatively prime]. = 2.
The number of generators of a cyclic group of order 12 is ________.
Correct answer is '4'. Can you explain this answer?
The number of generators of a cyclic group of order 12 is ________.

|
Pijush De answered • Feb 27, 2021 |
Use Euler's phi function as follows :
Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n and denoted by Greek letter phi as φ(n). The number of generators of a cyclic group can be found using Euler's phi function.
So here φ(12) = φ(4)×φ(3) [as 3 & 4 are relatively prime]. = 2 × 2
= 4.
Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n and denoted by Greek letter phi as φ(n). The number of generators of a cyclic group can be found using Euler's phi function.
So here φ(12) = φ(4)×φ(3) [as 3 & 4 are relatively prime]. = 2 × 2
= 4.

|
Pijush De upvoted • Jul 01, 2020 |
Which amongst the following statements is not true? - a)If
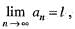 , then l is the only lim it point of <an>
, then l is the only lim it point of <an> - b)If l is the only limit point of < an >, then

- c)Every bounded sequence has a limit point
- d)The set of limit points of a bounded sequence is bounded
Correct answer is option 'A'. Can you explain this answer?
Which amongst the following statements is not true?
a)
If 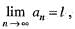 , then l is the only lim it point of <an>
, then l is the only lim it point of <an>
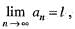 , then l is the only lim it point of <an>
, then l is the only lim it point of <an>b)
If l is the only limit point of < an >, then 

c)
Every bounded sequence has a limit point
d)
The set of limit points of a bounded sequence is bounded

|
Infinity Mathematics Cha answered |
Correct answer is b
<1,1,2,1 ,3,1/3="">
is a sequence which has only one limit point but not cgt
<1,1,2,1 ,3,1/3="">
is a sequence which has only one limit point but not cgt

|
Pijush De upvoted • Jun 19, 2020 |
If f(x) is differentiable on interval l and 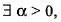 such that |f'(x)| ≤ a on l, then f(x) is
such that |f'(x)| ≤ a on l, then f(x) is- a) Continuous but not uniformly continuous on l
- b)Uniformly continuous but not continuous on l
- c)Uniformly continuous but not differentiable on l
- d)Continuous, uniformly continuous and differentiable on l
Correct answer is option 'A'. Can you explain this answer?
If f(x) is differentiable on interval l and 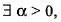 such that |f'(x)| ≤ a on l, then f(x) is
such that |f'(x)| ≤ a on l, then f(x) is
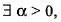 such that |f'(x)| ≤ a on l, then f(x) is
such that |f'(x)| ≤ a on l, then f(x) isa)
Continuous but not uniformly continuous on l
b)
Uniformly continuous but not continuous on l
c)
Uniformly continuous but not differentiable on l
d)
Continuous, uniformly continuous and differentiable on l
|
|
Chirag Verma answered |
For xy ∈ l, by Lagrange’s mean value theorem
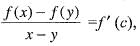 where x < c < y
where x < c < y
implies f(x)- f(y) = (x - y) f '(c )
implies |f(x) - f(y) | = x - y || f'(c)|
for a given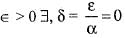 such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.
such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.
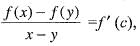 where x < c < y
where x < c < yimplies f(x)- f(y) = (x - y) f '(c )
implies |f(x) - f(y) | = x - y || f'(c)|
for a given
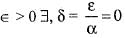 such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.
such that |f(x) - f(y)| < ε, x, y ∈ l. Hence f(x) is uniformly continuous on l. We know that every uniformly continuous function is also continuous.

|
Pijush De upvoted • Jun 19, 2020 |
A function f : R → R, defined by f(x) = 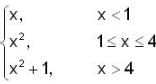
If T = {f(x) ; x ∈ R}, then the inverse function 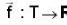
- a)Exist but not unique
- b)Exist and continuous on T
- c)Exist but not continuous on T
- d)Exist and differentiable on T
Correct answer is option 'B'. Can you explain this answer?
A function f : R → R, defined by f(x) = 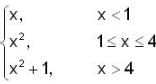
If T = {f(x) ; x ∈ R}, then the inverse function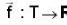
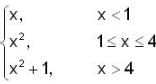
If T = {f(x) ; x ∈ R}, then the inverse function
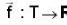
a)
Exist but not unique
b)
Exist and continuous on T
c)
Exist but not continuous on T
d)
Exist and differentiable on T
|
|
Chirag Verma answered |
The graph of the function is given by
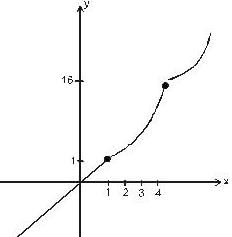



Fetching relevant content for you











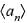 is convergent and
is convergent and 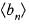 is not convergent
is not convergent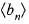 diverges to ∞
diverges to ∞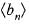 does not converges to 0
does not converges to 0 converges to 0
converges to 0 














