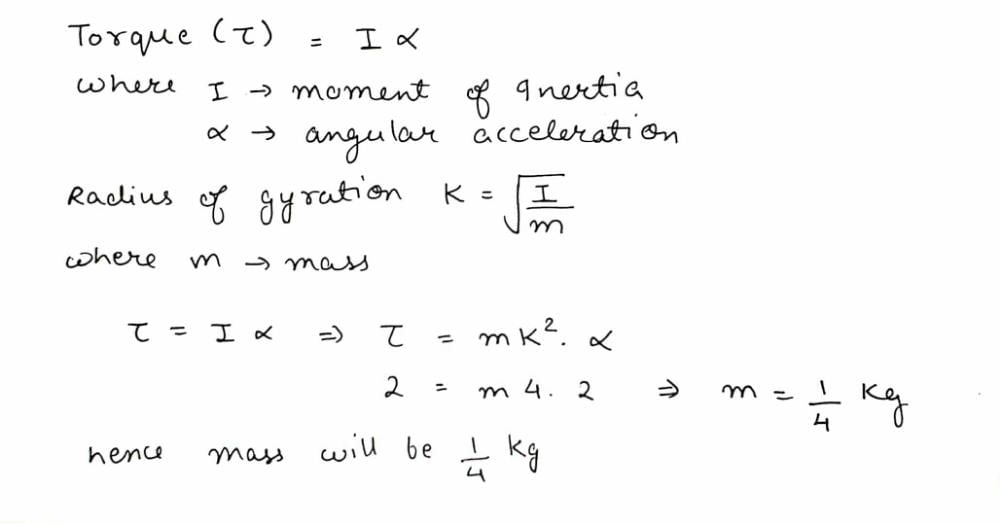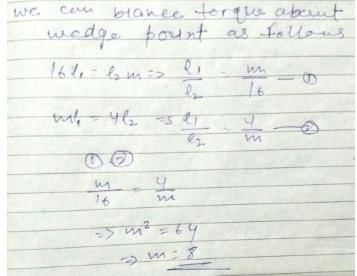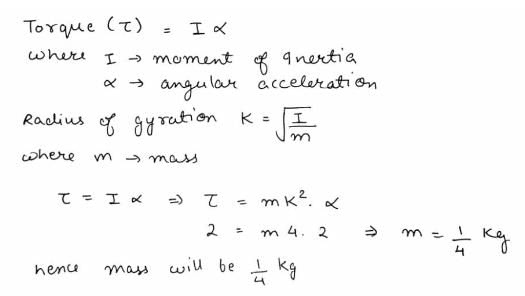All Exams >
JEE >
Weekly Tests for JEE Preparation >
All Questions
All questions of August Week 2 for JEE Exam
A right triangular plate ABC of mass m is free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is :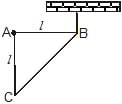 
- a)
- b)
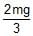
- c)
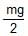
- d)mg
Correct answer is option 'B'. Can you explain this answer?
A right triangular plate ABC of mass m is free to rotate in the vertical plane about a fixed horizontal axis through A. It is supported by a string such that the side AB is horizontal. The reaction at the support A is :
a)
b)
c)
d)
mg
|
Crafty Classes answered |
The distance of Centre Of Mass of the given right angled triangle is 2L/3 along BA and L/3 along AC from the point B.
Force of magnitude mg is acting downwards at its COM.
Moment balance around B gives:
mg(2L/3)−FA(L)=0
(Moment= × =rFsin(θ)=F(rsin(θ))=Fr⊥)
∴FA=2mg/3
Force of magnitude mg is acting downwards at its COM.
Moment balance around B gives:
mg(2L/3)−FA(L)=0
(Moment= × =rFsin(θ)=F(rsin(θ))=Fr⊥)
∴FA=2mg/3
A homogeneous cubical brick lies motionless on a rough inclined surface. The half of the brick which applies greater pressure on the plane is :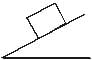 
- a) Left half
- b)Right half
- c)Both applies equal pressure
- d)The answer depend upon coefficient of friction
Correct answer is option 'A'. Can you explain this answer?
A homogeneous cubical brick lies motionless on a rough inclined surface. The half of the brick which applies greater pressure on the plane is :
a)
Left half
b)
Right half
c)
Both applies equal pressure
d)
The answer depend upon coefficient of friction
|
Mohit Rajpoot answered |
As weight of the body (mg) acts along the left side i.e. mg sinx acts along flow of object.
mgcosx acts perpendicular to flow of the object.
The pressure of right half comes on left half hence left half has maximum pressure.
mgcosx acts perpendicular to flow of the object.
The pressure of right half comes on left half hence left half has maximum pressure.
A solid sphere and a hollow sphere of the same mass have the same moments of inertia about their respective diameters, the ratio of their radii is- a)(5)1/2 : (3)1/2
- b) (3)1/2 : (5)1/2
- c)3 : 2
- d)2 : 3
Correct answer is option 'A'. Can you explain this answer?
A solid sphere and a hollow sphere of the same mass have the same moments of inertia about their respective diameters, the ratio of their radii is
a)
(5)1/2 : (3)1/2
b)
(3)1/2 : (5)1/2
c)
3 : 2
d)
2 : 3
|
Gaurav Kumar answered |
We know moment of inertia of solid sphere Is=2/5msRs2 and
moment of inertia of hollow sphere IH=2/3mHRH2 As per question Is=IH
Now,
2/5msRs2=2/3mHRH2
as the masses are equal the ratio of their radii will be
Rs2 /RH2 =2/3/2/5=√5/3=(5)1/2: (3)1/2
moment of inertia of hollow sphere IH=2/3mHRH2 As per question Is=IH
Now,
2/5msRs2=2/3mHRH2
as the masses are equal the ratio of their radii will be
Rs2 /RH2 =2/3/2/5=√5/3=(5)1/2: (3)1/2
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4 kg m2.- a)12 kg m2
- b)3 kg m2
- c)6 kg m2
- d)9 kg m2
Correct answer is option 'C'. Can you explain this answer?
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4 kg m2.
a)
12 kg m2
b)
3 kg m2
c)
6 kg m2
d)
9 kg m2
|
Naina Sharma answered |
At tangent I =MR2/2 + MR2 --- (1)
MR2/2 = 4, MR2 = 8 then substitute in (1) you will get I = 12, this is for tangent perpendicular to plane then divide by 2 you will get tangent along the plane
MR2/2 = 4, MR2 = 8 then substitute in (1) you will get I = 12, this is for tangent perpendicular to plane then divide by 2 you will get tangent along the plane
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is- a)4 unit
- b)6 unit
- c)8 unit
- d)10 unit
Correct answer is option 'D'. Can you explain this answer?
The M.I. of a disc about its diameter is 2 units. Its M.I. about axis through a point on its rim and in the plane of the disc is
a)
4 unit
b)
6 unit
c)
8 unit
d)
10 unit
|
Krishna Iyer answered |
We know that for a disc of mass m and radius r
MI of a disc about its diameter = mr2/4 = 2
And also MI about a point on its rim = mr2/4 + mr2
= 5mr2/4
= 5 x 2 = 10
MI of a disc about its diameter = mr2/4 = 2
And also MI about a point on its rim = mr2/4 + mr2
= 5mr2/4
= 5 x 2 = 10
The moment of inertia and rotational kinetic energy of a fly wheel are 20kg-m2 and 1000 joule respectively. Its angular frequency per minute would be -- a)600/π
- b)25/π2
- c)5/π
- d)300/π
Correct answer is option 'D'. Can you explain this answer?
The moment of inertia and rotational kinetic energy of a fly wheel are 20kg-m2 and 1000 joule respectively. Its angular frequency per minute would be -
a)
600/π
b)
25/π2
c)
5/π
d)
300/π
|
Riya Banerjee answered |
Rotational K.E. = ½ × moment of inertia × square of angular velocity = ½Iw2
An automobile engine develops 100H.P. when rotating at a speed of 1800 rad/min. The torque it delivers is- a)3.33 W-s
- b)200W-s
- c)248.7 W-s
- d)2487 W-s
Correct answer is option 'D'. Can you explain this answer?
An automobile engine develops 100H.P. when rotating at a speed of 1800 rad/min. The torque it delivers is
a)
3.33 W-s
b)
200W-s
c)
248.7 W-s
d)
2487 W-s
|
Manish Aggarwal answered |
100 HP = 74570 W or 74.57 KW Now, P = 2*π*N*T/60 where, P is the power (in W), N is the operating speed of the engine (in r.p.m.) and T is the Torque (in N.m). Therefore, 74570 = 2*π*1800*T/60 i.e. T = 395.606 N.m
Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be 
- a)
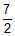PQ2 - b)
PQ2 - c)
PQ2 - d)
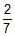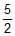PQ2
Correct answer is option 'A'. Can you explain this answer?
Three rings, each of mass P and radius Q are arranged as shown in the figure. The moment of inertia of the arrangement about YY' axis will be
a)
PQ2b)
PQ2c)
PQ2d)
PQ2
|
Lohit Matani answered |
For ring 1
(MOI)1 = MOI about diameter + PQ2
MOI about diameter = ½ PQ2
(MOI)1 = 3/2 PQ2
Similarly, (MOI)2 = 3/2 PQ2
(MOI)3 = ½ PQ2
Total MOI = 7/2 PQ2
(MOI)1 = MOI about diameter + PQ2
MOI about diameter = ½ PQ2
(MOI)1 = 3/2 PQ2
Similarly, (MOI)2 = 3/2 PQ2
(MOI)3 = ½ PQ2
Total MOI = 7/2 PQ2
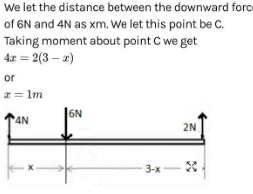
A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total length of the rod AB = 3m. To keep the rod in equilibrium a force of 6N should act in the following manner :- a)Downwards at any point between A and B.
- b) Downwards at mid point of AB.
- c)Downwards at a point C such that AC = 1m.
- d) Downwards at a point D such that BD = 1m.
Correct answer is option 'D'. Can you explain this answer?
A weightless rod is acted on by upward parallel forces of 2N and 4N ends A and B respectively. The total length of the rod AB = 3m. To keep the rod in equilibrium a force of 6N should act in the following manner :
a)
Downwards at any point between A and B.
b)
Downwards at mid point of AB.
c)
Downwards at a point C such that AC = 1m.
d)
Downwards at a point D such that BD = 1m.
|
|
Riya Banerjee answered |
The moment of inertia of a body depends upon -- a) mass only
- b) angular velocity only
- c)distribution of particles only
- d)mass and distribution of mass about the axis
Correct answer is option 'D'. Can you explain this answer?
The moment of inertia of a body depends upon -
a)
mass only
b)
angular velocity only
c)
distribution of particles only
d)
mass and distribution of mass about the axis
|
Preeti Iyer answered |
I = mr2, therefore it depends on body mass and its mass distribution.
A wheel starting with angular velocity of 10 radian/sec acquires angular velocity of 100 radian/sec in 15 seconds. If moment of inertia is 10kg-m2, then applied torque (in newton-metre) is- a)900
- b)100
- c)90
- d)60
Correct answer is option 'D'. Can you explain this answer?
A wheel starting with angular velocity of 10 radian/sec acquires angular velocity of 100 radian/sec in 15 seconds. If moment of inertia is 10kg-m2, then applied torque (in newton-metre) is
a)
900
b)
100
c)
90
d)
60
|
|
Gaurav Kumar answered |
I(ωf - ωi)/t = τ
Hence, τ = 60
Hence, τ = 60
Consider the following statementsAssertion (A) : The moment of inertia of a rigid body reduces to its minimum value as compared to any other parallel axis when the axis of rotation passes through its centre of mass.Reason (R) : The weight of a rigid body always acts through its centre of mass in uniform gravitational field. Of these statements :- a)both A and R are true and R is the correct explanation of A
- b) both A and R are true but R is not a correct explanation of A
- c)A is true but R is false
- d) A is false but R is true
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements
Assertion (A) : The moment of inertia of a rigid body reduces to its minimum value as compared to any other parallel axis when the axis of rotation passes through its centre of mass.
Reason (R) : The weight of a rigid body always acts through its centre of mass in uniform gravitational field. Of these statements :
a)
both A and R are true and R is the correct explanation of A
b)
both A and R are true but R is not a correct explanation of A
c)
A is true but R is false
d)
A is false but R is true
|
|
Neha Joshi answered |
Moment of inertia about its centroidal axis has a minimum value as the centroidal axis has mass evenly distributed around it thereby providing minimum resistance to rotation as compared to any other axis. Also the statement-2 is correct but is not the correct explanation for statement-1.
On applying a constant torque on a body- a) Linear velocity may be increases
- b)Angular velocity may be increases
- c)It will rotate with constant angular velocity
- d)It will move with constant velocity
Correct answer is option 'A'. Can you explain this answer?
On applying a constant torque on a body
a)
Linear velocity may be increases
b)
Angular velocity may be increases
c)
It will rotate with constant angular velocity
d)
It will move with constant velocity
|
|
Geetika Shah answered |
If a constant torque is applied it is possible that a positive angular acceleration gets generated which can generate a positive acceleration and hence increasing both velocity and angular velocity.
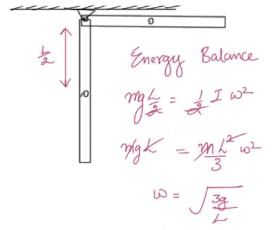
One end of a uniform rod of mass m and length I is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity w. The force exerted by the clamp on the rod has a horizontal component- a)mw2l
- b)zero
- c) mg
- d)
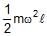
Correct answer is option 'D'. Can you explain this answer?
One end of a uniform rod of mass m and length I is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity w. The force exerted by the clamp on the rod has a horizontal component
a)
mw2l
b)
zero
c)
mg
d)
|
|
Raghav Bansal answered |
Consider a rod of length l and mass m rotating with an angular velocity of w
dF = dm l w2
dF = (m/l) dμ l w2
Integrating
F = ½mlw2
dF = dm l w2
dF = (m/l) dμ l w2
Integrating
F = ½mlw2
A disc of radius 2m and mass 200kg is acted upon by a torque 100N-m. Its angular acceleration would be- a) 1 rad/sec2
- b)0.25 rad/sec2
- c)0.5 rad/sec2
- d)2 rad/sec2.
Correct answer is option 'B'. Can you explain this answer?
A disc of radius 2m and mass 200kg is acted upon by a torque 100N-m. Its angular acceleration would be
a)
1 rad/sec2
b)
0.25 rad/sec2
c)
0.5 rad/sec2
d)
2 rad/sec2.
|
|
Neha Joshi answered |
F = ma
a = Wr
So, F = mwr
a = wr = acceleration
m = 200kg
F = 100 n-m, r = 2m, w = to be calculated
100 = 200 x w2
w = 0.25 rad/sec2
a = Wr
So, F = mwr
a = wr = acceleration
m = 200kg
F = 100 n-m, r = 2m, w = to be calculated
100 = 200 x w2
w = 0.25 rad/sec2
Two spheres of same mass and radius are in contact with each other. If the moment of inertia of a sphere about its diameter is I, then the moment of inertia of both the spheres about the tangent at their common point would be -- a)3I
- b)7I
- c)4I
- d)5I
Correct answer is option 'B'. Can you explain this answer?
Two spheres of same mass and radius are in contact with each other. If the moment of inertia of a sphere about its diameter is I, then the moment of inertia of both the spheres about the tangent at their common point would be -
a)
3I
b)
7I
c)
4I
d)
5I
|
|
Geetika Shah answered |
The moment of inertia of a sphere about its diameter is given as,
I=2/5 MR2
The moment of inertia of the sphere about the tangent is given as,
I′=2/5MR2+MR2
I′=7/5MR2
The total moment of inertia of both spheres about the common tangent is given as,
It=2I′
It=2×7/5MR2
It=7I
I=2/5 MR2
The moment of inertia of the sphere about the tangent is given as,
I′=2/5MR2+MR2
I′=7/5MR2
The total moment of inertia of both spheres about the common tangent is given as,
It=2I′
It=2×7/5MR2
It=7I
A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is- a) IA > IB
- b)IA = IB
- c) IA < IB
- d) depends on the actual values of t and r.
Correct answer is option 'C'. Can you explain this answer?
A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is
a)
IA > IB
b)
IA = IB
c)
IA < IB
d)
depends on the actual values of t and r.
|
Lavanya Menon answered |
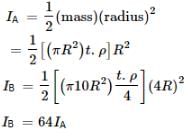
Moment of inertia of a thin semicircular disc (mass = M & radius = R) about an axis through point O and perpendicular to plane of disc, is given by :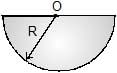 
- a)
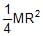
- b)
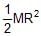
- c)
- d)MR2
Correct answer is option 'B'. Can you explain this answer?
Moment of inertia of a thin semicircular disc (mass = M & radius = R) about an axis through point O and perpendicular to plane of disc, is given by :
a)
b)
c)
d)
MR2
|
|
Geetika Shah answered |
Mass of semicircular disc = M
Suppose there is a circular disc of mass 2M, then
Moment of intertia of circular disc = ½ (2M)R2
Moment of intertia of circular disc = ½ (2M)R2 = MR2
=> So, Moment of intertia of semi-circular disc = ½ MR2
Suppose there is a circular disc of mass 2M, then
Moment of intertia of circular disc = ½ (2M)R2
Moment of intertia of circular disc = ½ (2M)R2 = MR2
=> So, Moment of intertia of semi-circular disc = ½ MR2
For the same total mass which of the following will have the largest moment of inertia about an axis passing through its centre of mass and perpendicular to the plane of the body- a)a disc of radius a
- b) a ring of radius a
- c)a square lamina of side 2a
- d) four rods forming a square of side 2a
Correct answer is option 'D'. Can you explain this answer?
For the same total mass which of the following will have the largest moment of inertia about an axis passing through its centre of mass and perpendicular to the plane of the body
a)
a disc of radius a
b)
a ring of radius a
c)
a square lamina of side 2a
d)
four rods forming a square of side 2a
|
Lyrics Master answered |
Moment of inertia depends on distribution of mass around axis...the more the mass near the axis less the moment of inertia...four rods forming a square has less more moment of inertia because of less mass ner axis
A disc of metal is melted to recast in the form of a solid sphere. The moment of inertias about a vertical axis passing through the centre would -- a) decrease
- b)increase
- c) remains same
- d)nothing can be said
Correct answer is option 'A'. Can you explain this answer?
A disc of metal is melted to recast in the form of a solid sphere. The moment of inertias about a vertical axis passing through the centre would -
a)
decrease
b)
increase
c)
remains same
d)
nothing can be said
|
|
Rajesh Gupta answered |
Moment of inertia will decrease, because
Id=1/2mr2 and Is=2/5mr2,
the radius of sphere formed on recasting the disc will also decrease.
Id=1/2mr2 and Is=2/5mr2,
the radius of sphere formed on recasting the disc will also decrease.
A stone of mass 4kg is whirled in a horizontal circle of radius 1m and makes 2 rev/sec. The moment of inertia of the stone about the axis of rotation is- a) 64 kg × m2
- b) 4 kg × m2
- c)16 kg × m2
- d)1 kg × m2
Correct answer is option 'B'. Can you explain this answer?
A stone of mass 4kg is whirled in a horizontal circle of radius 1m and makes 2 rev/sec. The moment of inertia of the stone about the axis of rotation is
a)
64 kg × m2
b)
4 kg × m2
c)
16 kg × m2
d)
1 kg × m2
|
|
Preeti Iyer answered |
By using the Basic formula i.e I = MR^2
Where M = 4Kg , R = 1m
I = 4 x 1 ^2 = 4Kg/m^2
A particle is at a distance r from the axis of rotation. A given torque t produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is- a)t/2
- b)t
- c)2t
- d)4t
Correct answer is option 'A'. Can you explain this answer?
A particle is at a distance r from the axis of rotation. A given torque t produces some angular acceleration in it. If the mass of the particle is doubled and its distance from the axis is halved, the value of torque to produce the same angular acceleration is
a)
t/2
b)
t
c)
2t
d)
4t
|
|
Divyansh Saha answered |
We know that from some torque t, angular acceleration a produced can be find by,
t = I a, where I is moment of inertia = mr2
Thus we get a = t / mr2
Now we have 2m and r/2
Thus a = t / mr2 = T / 2m(r/2)2
Thus we get T = t/2
t = I a, where I is moment of inertia = mr2
Thus we get a = t / mr2
Now we have 2m and r/2
Thus a = t / mr2 = T / 2m(r/2)2
Thus we get T = t/2
A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is- a)vertical
- b) horizontal and skew with the axis
- c)horizontal and intersecting the axis
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
a)
vertical
b)
horizontal and skew with the axis
c)
horizontal and intersecting the axis
d)
none of these
|
|
Amrutha Das answered |
Since the axis is vertical, the force will be horizontal and since it is centripetal force it will intersect the axis.
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is- a)Mr2
- b)
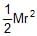
- c)
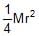
- d)
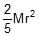
Correct answer is option 'A'. Can you explain this answer?
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is
a)
Mr2
b)
c)
d)
|
Suresh Reddy answered |
The formula for the MOI of a uniform semicircular ring about a perpendicular line is ½ Mr2
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.- a)IA < IB
- b) If IA < IB, the axes are parallel.
- c) If the axes are parallel, IA < IB
- d)If the axes are not parallel, IA ³ IB
Correct answer is option 'C'. Can you explain this answer?
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
a)
IA < IB
b)
If IA < IB, the axes are parallel.
c)
If the axes are parallel, IA < IB
d)
If the axes are not parallel, IA ³ IB
|
EduRev Humanities answered |
If the axes are parallel, we use the formula:
Io = Icm + md2
For the first body the distance between the axis and the axis passing through C.O.M is 0
Therefore, Io = Icm + m(0)2 = lcm since it is mentioned in question
Whereas for the second body it is not passing through the C.O.M therefore, there is some distance between the axes, say 'd'
So, Io = Icm + md2
Io = Icm + md2
For the first body the distance between the axis and the axis passing through C.O.M is 0
Therefore, Io = Icm + m(0)2 = lcm since it is mentioned in question
Whereas for the second body it is not passing through the C.O.M therefore, there is some distance between the axes, say 'd'
So, Io = Icm + md2
Consider the following statementsAssertion (A) : A cyclist always bends inwards while negotiating a curveReason (R) : By bending he lowers his centre of gravity Of these statements,- a) Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is not the correct explanation of A
- c) A is true but R is false
- d)A is false but R is true
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements
Assertion (A) : A cyclist always bends inwards while negotiating a curve
Reason (R) : By bending he lowers his centre of gravity Of these statements,
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is not the correct explanation of A
c)
A is true but R is false
d)
A is false but R is true
|
|
Pranavi Banerjee answered |
B is correct. The reason is a part of the question.
A rigid body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of inertia is given byI = 2x2 - 12x + 27 The x-coordinate of centre of mass is- a) x = 2
- b)x = 0
- c)x = 1
- d)x = 3
Correct answer is option 'D'. Can you explain this answer?
A rigid body can be hinged about any point on the x-axis. When it is hinged such that the hinge is at x, the moment of inertia is given by
I = 2x2 - 12x + 27 The x-coordinate of centre of mass is
a)
x = 2
b)
x = 0
c)
x = 1
d)
x = 3
|
|
Preeti Iyer answered |
Moment of inertia is minimum at centre of mass of the body.
I=minimum for centre of mass
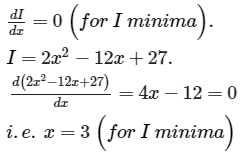
Therefore x co-ordinate of centre of mass is 3 unit.
Chapter doubts & questions for August Week 2 - Weekly Tests for JEE Preparation 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of August Week 2 - Weekly Tests for JEE Preparation in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily