All Exams >
JEE >
Weekly Tests for JEE Preparation >
All Questions
All questions of May Week 2 for JEE Exam
Two equipotential surfaces have a potential of -10V and 90V respectively, what is the difference in potential between these surfaces?- a)90V
- b)80V
- c)0V
- d)100V
Correct answer is 'D'. Can you explain this answer?
Two equipotential surfaces have a potential of -10V and 90V respectively, what is the difference in potential between these surfaces?
a)
90V
b)
80V
c)
0V
d)
100V
|
|
Krishna Iyer answered |
Potential = high potential - low potential
so our high potential is 90V and low potential is 10V,
potential = 90-(-10)=100V
so our high potential is 90V and low potential is 10V,
potential = 90-(-10)=100V
The number of all possible matrices of order 3×3 with each entry 0 if 1 is- a)81
- b)512
- c)18
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The number of all possible matrices of order 3×3 with each entry 0 if 1 is
a)
81
b)
512
c)
18
d)
none of these
|
|
Harsh Majumdar answered |
To find the number of all possible matrices of order 3, we need to consider the number of choices for each entry in the matrix.
In a matrix of order 3, there are 9 entries. Each entry can be chosen from any number in the set {0, 1, 2, ..., 9} since there are no restrictions mentioned. Therefore, there are 10 choices for each entry.
Since each entry can be chosen independently, we can use the multiplication principle to find the total number of matrices. This principle states that if there are n choices for one event and m choices for another event, then there are n * m choices for both events together.
Applying this principle to our matrix, we have 10 choices for each of the 9 entries. Therefore, the total number of possible matrices of order 3 is 10^9.
Hence, the number of all possible matrices of order 3 is 10^9.
In a matrix of order 3, there are 9 entries. Each entry can be chosen from any number in the set {0, 1, 2, ..., 9} since there are no restrictions mentioned. Therefore, there are 10 choices for each entry.
Since each entry can be chosen independently, we can use the multiplication principle to find the total number of matrices. This principle states that if there are n choices for one event and m choices for another event, then there are n * m choices for both events together.
Applying this principle to our matrix, we have 10 choices for each of the 9 entries. Therefore, the total number of possible matrices of order 3 is 10^9.
Hence, the number of all possible matrices of order 3 is 10^9.
The value of λ, for which system of equations. x + y + z = 1, x + 2y + 2z = 3, x + 2y + λz = 4, have no solution is
- a)1
- b)2
- c)0
- d)3
Correct answer is option 'B'. Can you explain this answer?
The value of λ, for which system of equations. x + y + z = 1, x + 2y + 2z = 3, x + 2y + λz = 4, have no solution is
a)
1
b)
2
c)
0
d)
3
|
|
Kiran Sengupta answered |
This question is unclear as there is no context or information provided. Please provide more details for me to give a relevant answer.
When a positive charge is moved in an electrostatic field from a point at high potential to a low potential, its kinetic energy- a)Remains constant
- b)Decreases
- c)Increases
- d)Either increase or remain constant
Correct answer is option 'C'. Can you explain this answer?
When a positive charge is moved in an electrostatic field from a point at high potential to a low potential, its kinetic energy
a)
Remains constant
b)
Decreases
c)
Increases
d)
Either increase or remain constant

|
Siddhi Bhardwaj answered |
You can generalise it by assuming a positive charge moving away from another positive charge. now both of them are repelling each other with some force. so that positive charge will accelerate which results in the increase in K.E.
The shape of equipotential surface for an infinite line charge is:- a)Coaxial cylindrical surfaces
- b)Parallel plane surfaces
- c)Parallel plane surfaces perpendicular to lines of force
- d)None of above
Correct answer is option 'A'. Can you explain this answer?
The shape of equipotential surface for an infinite line charge is:
a)
Coaxial cylindrical surfaces
b)
Parallel plane surfaces
c)
Parallel plane surfaces perpendicular to lines of force
d)
None of above
|
|
Rajesh Gupta answered |
The shape of equipotential surface for an infinite line charge is coaxial cylindrical because A curved surface on which potential is constant is equipotential curve . If we consider the line charge then the focus of the point should have the same potential hence it is a coaxial cylinder.
If A and B are square matrices of the same order, then(A+B)2 = A2+2AB+B2 implies- a)AB + BA = O
- b)AB = O
- c)AB = BA
- d)none of these.
Correct answer is 'A'. Can you explain this answer?
If A and B are square matrices of the same order, then(A+B)2 = A2+2AB+B2 implies
a)
AB + BA = O
b)
AB = O
c)
AB = BA
d)
none of these.

|
Samridhi Bajaj answered |
If A and B are square matrices of same order , then , product of the matrices is not commutative.Therefore , the given result is true only when AB = BA.
Equipotential surfaces cannot- a)be parallel
- b)be spherical
- c)Intersect
- d)be irregularly shaped.
Correct answer is option 'C'. Can you explain this answer?
Equipotential surfaces cannot
a)
be parallel
b)
be spherical
c)
Intersect
d)
be irregularly shaped.
|
|
Krishna Iyer answered |
The electric field lines are perpendicular to the equipotential surface. The field lines can not intersect each other because the electric force can not have two directions at a point.
A metal sphere carries a charge of 5×10-8C and is at a potential of 200 V, relative to the potential far away. The potential at the centre of the sphere is:- a)-100V
- b)0
- c)200V
- d)2×10-6v
Correct answer is option 'C'. Can you explain this answer?
A metal sphere carries a charge of 5×10-8C and is at a potential of 200 V, relative to the potential far away. The potential at the centre of the sphere is:
a)
-100V
b)
0
c)
200V
d)
2×10-6v
|
|
Keerthana Iyer answered |
Given data:
Charge on the sphere, q = 5.1 × 10⁻⁸ C
Potential difference, V = 200 V
We know that the formula for potential difference is:
V = kq/r
where k is Coulomb's constant, q is the charge on the sphere and r is the radius of the sphere.
Calculating the radius of the sphere:
r = kq/V
r = (9 × 10^9 Nm^2/C^2 × 5.1 × 10⁻⁸ C) / (200 V)
r = 2.295 × 10⁻⁴ m
The potential at the centre of the sphere is given by:
V' = kq/R
where R is the radius of the sphere.
As the point is at the centre of the sphere, R = r.
V' = kq/r
V' = (9 × 10^9 Nm^2/C^2 × 5.1 × 10⁻⁸ C) / (2.295 × 10⁻⁴ m)
V' = 2 × 10² V
Therefore, the potential at the centre of the sphere is 200 V (option C).
Charge on the sphere, q = 5.1 × 10⁻⁸ C
Potential difference, V = 200 V
We know that the formula for potential difference is:
V = kq/r
where k is Coulomb's constant, q is the charge on the sphere and r is the radius of the sphere.
Calculating the radius of the sphere:
r = kq/V
r = (9 × 10^9 Nm^2/C^2 × 5.1 × 10⁻⁸ C) / (200 V)
r = 2.295 × 10⁻⁴ m
The potential at the centre of the sphere is given by:
V' = kq/R
where R is the radius of the sphere.
As the point is at the centre of the sphere, R = r.
V' = kq/r
V' = (9 × 10^9 Nm^2/C^2 × 5.1 × 10⁻⁸ C) / (2.295 × 10⁻⁴ m)
V' = 2 × 10² V
Therefore, the potential at the centre of the sphere is 200 V (option C).
The value of electric field vector 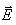 along the surface of constant potential of 100 V
along the surface of constant potential of 100 V- a)100 V/m
- b)-100 V/m
- c)10 V/m
- d)Zero
Correct answer is option 'D'. Can you explain this answer?
The value of electric field vector 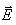 along the surface of constant potential of 100 V
along the surface of constant potential of 100 V
a)
100 V/m
b)
-100 V/m
c)
10 V/m
d)
Zero
|
|
Anjana Sharma answered |
As we know that electric field is in reverse sense of the directional gradient of electric potential, so if V is constant, E should be zero. So, for E to be zero, either V has to be zero, or constant, or the 3 directional derivative components of V must cancel out each other in space. So we cant claim that V always has to be zero, if E is zero in a region, since E is a vector & V is a scalar quantity. But if V is zero, then surely E has to be zero; the reverse case is not true always.
hope it was helpful...
I2 is the matrix- a)
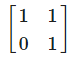
- b)
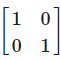
- c)
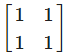
- d)
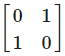
Correct answer is option 'B'. Can you explain this answer?
I2 is the matrix
a)
b)
c)
d)

|
Divey Sethi answered |
In linear algebra, the identity matrix, or sometimes ambiguously called a unit matrix, of size n is the n × n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context
For what value of λ the following system of equations does not have a solution ? x + y + z = 6, 4x + λy - λz = 0, 3 x + 2y – 4 z = - 5- a)0
- b)3
- c)-3
- d)1.
Correct answer is option 'B'. Can you explain this answer?
For what value of λ the following system of equations does not have a solution ? x + y + z = 6, 4x + λy - λz = 0, 3 x + 2y – 4 z = - 5
a)
0
b)
3
c)
-3
d)
1.

|
Shivani answered |
Find determinant of coefficients of the eqns given....and equal tht to zero....u ll get the ans...HOPE U GOT IT...
Shape of equipotential surfaces for a uniform electric field along x-axis are- a)Planes along x-z direction
- b)Planes along x-y direction
- c)Planes normal to field
- d)Concentric spherical shells
Correct answer is option 'C'. Can you explain this answer?
Shape of equipotential surfaces for a uniform electric field along x-axis are
a)
Planes along x-z direction
b)
Planes along x-y direction
c)
Planes normal to field
d)
Concentric spherical shells
|
|
Swati Verma answered |
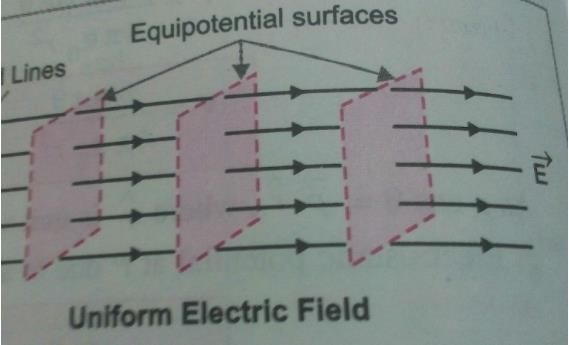
Shape of equipotential surfaces for a uniform electric field along x-axis are Planes normal to the field.
Optical analogue of an equipotential surface is- a)Wavefront of light
- b)Wave motion of light
- c)Reflection of light
- d)Interference of light
Correct answer is option 'A'. Can you explain this answer?
Optical analogue of an equipotential surface is
a)
Wavefront of light
b)
Wave motion of light
c)
Reflection of light
d)
Interference of light
|
|
Rohit Shah answered |
Optical analogue of anequipotential surface is. Wavefronts are surfaces of constant phase. Similarly,equipotential surface due to point charge is spherical in shape and has same potential at each point on selected surface.
If A is a matrix of order 3 × 4 , then each row of A has- a)12 elements
- b)3 elements
- c)4 elements
- d)7 elements.
Correct answer is option 'C'. Can you explain this answer?
If A is a matrix of order 3 × 4 , then each row of A has
a)
12 elements
b)
3 elements
c)
4 elements
d)
7 elements.
|
|
Gaurav Kumar answered |

, therefore matrix A has 4 elements in each row
Let A be any m×n matrix, then A2 can be found only when- a)m < n
- b)m = n
- c)m > n
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
Let A be any m×n matrix, then A2 can be found only when
a)
m < n
b)
m = n
c)
m > n
d)
none of these.

|
Nikhil Sen answered |
The product of any matrix with itself can be found only when it is a square matrix.i.e. m = n.
If Ak = 0(A is nilpotent with index k), (I − A)p = I + A + A2 + … + Ak − 1, thus p is- a)−1
- b)−2
- c)1/2
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If Ak = 0(A is nilpotent with index k), (I − A)p = I + A + A2 + … + Ak − 1, thus p is
a)
−1
b)
−2
c)
1/2
d)
None of these

|
EduRev JEE answered |
Let B = I + A + A2 +…+ Ak − 1
Now multiply both sides by (I − A), we get B(I − A) = (I + A + A2 + …+ Ak − 1)(I − A)
= I − A + A − A2 + A2 − A3 +… − Ak−1+Ak−1−Ak
= I − Ak = I, since Ak = 0 ⇒ B = (I − A) − 1
Hence (I−A)−1 = I + A + A2 +…+ Ak−1
Thus p = −1
Now multiply both sides by (I − A), we get B(I − A) = (I + A + A2 + …+ Ak − 1)(I − A)
= I − A + A − A2 + A2 − A3 +… − Ak−1+Ak−1−Ak
= I − Ak = I, since Ak = 0 ⇒ B = (I − A) − 1
Hence (I−A)−1 = I + A + A2 +…+ Ak−1
Thus p = −1
A square matrix A = [aij]n×n is called a lower triangular matrix if aij = 0 for- a)i is less than j
- b)i = j
- c)iis greater than j
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
A square matrix A = [aij]n×n is called a lower triangular matrix if aij = 0 for
a)
i is less than j
b)
i = j
c)
iis greater than j
d)
none of these.

|
Ishita Reddy answered |
Lower triangular matrix is given by :
 , here , aij = 0
, here , aij = 0
if i is less than j.andaij ≠ 0, if i is greater than j.
 , here , aij = 0
, here , aij = 0if i is less than j.andaij ≠ 0, if i is greater than j.
If A is any square matrix, then- a)A+At is symmetric
- b)A−At is symmetric
- c)A+At is skew-symmetric
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
If A is any square matrix, then
a)
A+At is symmetric
b)
A−At is symmetric
c)
A+At is skew-symmetric
d)
none of these.

|
Harshitha Nambiar answered |
For every square matrix (A + A’) is always symmetric.
A square matrix A = [aij]n×n is called an upper triangular if aij = 0 for- a)i is less than j
- b)i = j
- c)i is greater than j
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A square matrix A = [aij]n×n is called an upper triangular if aij = 0 for
a)
i is less than j
b)
i = j
c)
i is greater than j
d)
none of these

|
Nikhil Sen answered |
Upper Triangular matrix is given by :
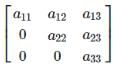 .
.
Here, aij=0 , if i is greater than j.and aij ≠ 0, if I is less than j.
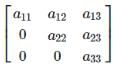 .
.Here, aij=0 , if i is greater than j.and aij ≠ 0, if I is less than j.
The equations, x + 4 y – 2 z = 3, 3 x + y + 5 z = 7, 2 x + 3y +z = 5 have- a)infinitely many solutions
- b)a unique solution
- c)no solution
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The equations, x + 4 y – 2 z = 3, 3 x + y + 5 z = 7, 2 x + 3y +z = 5 have
a)
infinitely many solutions
b)
a unique solution
c)
no solution
d)
none of these

|
Sanchita Iyer answered |
The given system of equations does not have solution if :

- 0 ⇒ 1(-14) - 4(-7) -2(7) = 0
If, we are given a square matrix A then, Adj.(KA) = ….
- a)KnAdj.A
- b)Kn−1Adj.A
- c)K Adj. A
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If, we are given a square matrix A then, Adj.(KA) = ….
a)
KnAdj.A
b)
Kn−1Adj.A
c)
K Adj. A
d)
None of these

|
Sahana Joshi answered |
Adj.(KA) = Kn−1 Adj.A , where K is a scalar and A is a n x n matrix.
If P is of order 2 × 3 and Q is of order 3 × 2, then PQ is of order- a)3 × 2
- b)2 × 3
- c)2 × 2
- d)3 × 3
Correct answer is option 'C'. Can you explain this answer?
If P is of order 2 × 3 and Q is of order 3 × 2, then PQ is of order
a)
3 × 2
b)
2 × 3
c)
2 × 2
d)
3 × 3

|
Nikhil Sen answered |
Here, matrix P is of order 2 × 3 and matrix Q is of order 2 × 2 , then , the product PQ is defined only when : no. of columns in P = no. of rows in Q. And the order of resulting matrix is given by : rows in P x columns in Q.
If A and B are any two matrices, then
- a)AB may or may not be defined.
- b)AB = O
- c)2A2
- d)A2 = O
Correct answer is option 'A'. Can you explain this answer?
If A and B are any two matrices, then
a)
AB may or may not be defined.
b)
AB = O
c)
2A2
d)
A2 = O
|
|
Kirti Mehta answered |
Explanation:
To understand why option A is the correct answer, we need to consider the properties of matrix multiplication.
Matrix Multiplication
When multiplying two matrices A and B, the number of columns in A must be equal to the number of rows in B. If this condition is not satisfied, then matrix multiplication is not defined.
Given that A and B are any two matrices, we cannot make any assumptions about their dimensions. Therefore, we cannot determine whether AB is defined or not without knowing the dimensions of A and B.
Option A: AB may or may not be defined
This option is correct because matrix multiplication is only defined when the dimensions of the matrices satisfy the condition mentioned above. Without knowing the dimensions of A and B, we cannot determine whether AB is defined or not. It is possible that AB is defined in some cases and not defined in others.
Option B: AB = O
This option is not always true. The zero matrix (O) is a matrix where all the elements are zero. It is possible for AB to be equal to O in some cases, but it is not a general result. The product of two matrices is not always the zero matrix.
Option C: 2A2
This option is not meaningful as it is not clear what is meant by "2A2". The notation "2A2" does not correspond to any valid matrix operation or expression.
Option D: A2 = O
This option is also not always true. The notation A2 typically represents the square of a matrix, which is obtained by multiplying the matrix by itself. It is possible for A2 to be equal to O in some cases, but it is not a general result. The square of a matrix is not always the zero matrix.
Therefore, the correct answer is option A. Without knowing the dimensions of A and B, we cannot determine whether AB is defined or not.
If A = [aij]n×n be a diagonal matrix with diagonal element all different and B = [bij]n×n be some another matrix. Let AB = [cij]n×n then cij is equal to- a)ajjbij
- b)aiibij
- c)aijbij
- d)aijbji
Correct answer is option 'B'. Can you explain this answer?
If A = [aij]n×n be a diagonal matrix with diagonal element all different and B = [bij]n×n be some another matrix. Let AB = [cij]n×n then cij is equal to
a)
ajjbij
b)
aiibij
c)
aijbij
d)
aijbji

|
Manish Aggarwal answered |
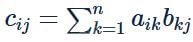 (In general) and in a diagonal matrix non-diagonal elements
(In general) and in a diagonal matrix non-diagonal elements
If A and B are two matrices such that AB = A and BA = B, then which one of the following is correct?- a)(AT)2 = AT
- b)(AT)2 = BT
- c)(AT)2 = (A − 1)−1
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If A and B are two matrices such that AB = A and BA = B, then which one of the following is correct?
a)
(AT)2 = AT
b)
(AT)2 = BT
c)
(AT)2 = (A − 1)−1
d)
None of the above

|
Learners Habitat answered |
Let A and B be two matrices such that AB = A and BA = B Now, consider AB = A Take Transpose on both side (AB)T = AT
⇒ AT = BT ⋅ AT ...(1)
Now, BA = B
Take, Transpose on both side (BA)T = BT
⇒ BT = AT⋅BT…(2)
Now, from equation (1) and (2). we have AT = (AT . BT)AT
AT=AT(BTAT)
= AT(AB)T(∵(AB)T = BT = BTAT)
= AT ⋅ AT
Thus, AT = (AT)2
⇒ AT = BT ⋅ AT ...(1)
Now, BA = B
Take, Transpose on both side (BA)T = BT
⇒ BT = AT⋅BT…(2)
Now, from equation (1) and (2). we have AT = (AT . BT)AT
AT=AT(BTAT)
= AT(AB)T(∵(AB)T = BT = BTAT)
= AT ⋅ AT
Thus, AT = (AT)2
Chapter doubts & questions for May Week 2 - Weekly Tests for JEE Preparation 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of May Week 2 - Weekly Tests for JEE Preparation in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup






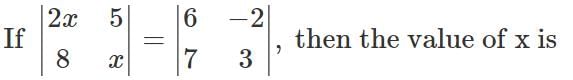
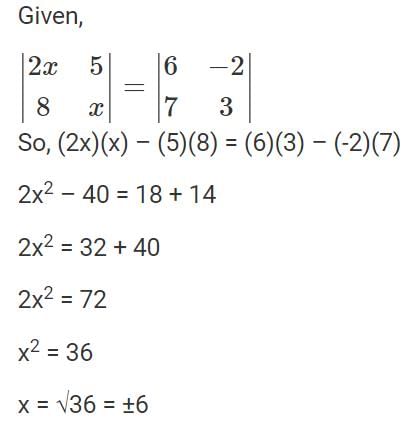
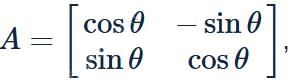 then AT+ A = I2, if
then AT+ A = I2, if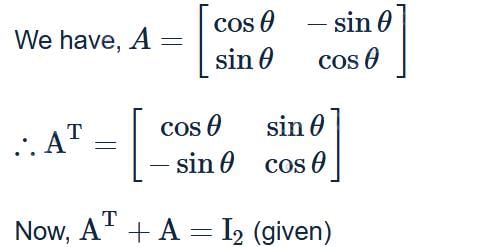
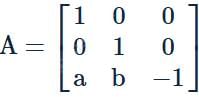 and I is the unit matrix of order 3, then A2 + 2 A4 + 4 A6 is equal to
and I is the unit matrix of order 3, then A2 + 2 A4 + 4 A6 is equal to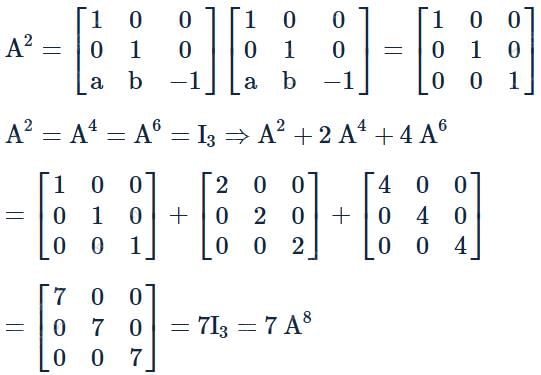

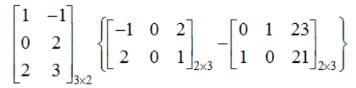
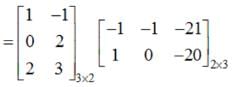
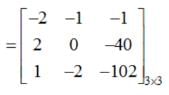
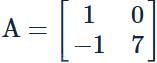 and
and 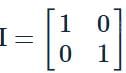 then the value of k so that A2 = 8 A + kI is
then the value of k so that A2 = 8 A + kI is