All Exams >
JEE >
Weekly Tests for JEE Preparation >
All Questions
All questions of December Week 3 for JEE Exam
Low Haemoglobin causes________.
- a)Malaria
- b)Anaemia
- c)Cancer
- d)Cholera
Correct answer is option 'B'. Can you explain this answer?
Low Haemoglobin causes________.
a)
Malaria
b)
Anaemia
c)
Cancer
d)
Cholera
|
|
Priyanka Sharma answered |
Hemoglobin, the substance that gives color to red blood cells, is the substance that allows for the transport of oxygen throughout the body. Low hemoglobin levels lead to anemia, which causes symptoms like fatigue and trouble breathing.
The differential equation,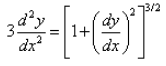 is a:
is a:
- a)second order, third degree equation.
- b)second order, second degree equation.
- c)third order, third degree equation.
- d)second order, first degree equation
Correct answer is option 'D'. Can you explain this answer?
The differential equation,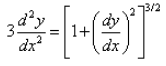 is a:
is a:
a)
second order, third degree equation.
b)
second order, second degree equation.
c)
third order, third degree equation.
d)
second order, first degree equation

|
Divey Sethi answered |
To calculate the degree or the order of a differential equation, the powers of derivatives should be an integer.
On squaring both sides, we get a differential equation with the integral power of derivatives.
On squaring both sides, we get a differential equation with the integral power of derivatives.
⇒ Order (the highest derivative) = 2
⇒ Degree (the power of highest degree) = 1
⇒ Degree (the power of highest degree) = 1
The differential equation 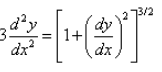 is a:
is a:- a)Third order, third degree equation
- b)Second order, second degree equation
- c)Second order, first degree equation
- d)Second order, third degree equation
Correct answer is option 'B'. Can you explain this answer?
The differential equation 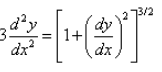 is a:
is a:
a)
Third order, third degree equation
b)
Second order, second degree equation
c)
Second order, first degree equation
d)
Second order, third degree equation
|
|
Suresh Iyer answered |
3*(d2y/dx2) = [1+(dy/dx)2]3/2
On squaring both side,
9*(d2y/dx2)2 = [1+(dy/dx)2]3
The order of the equation is 2. The power of the term determining the order determines the degree.
So, the degree is also 2.
On squaring both side,
9*(d2y/dx2)2 = [1+(dy/dx)2]3
The order of the equation is 2. The power of the term determining the order determines the degree.
So, the degree is also 2.
The differential equation for the equation  is :
is :- a)
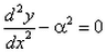
- b)
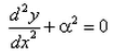
- c)
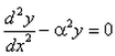
- d)
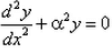
Correct answer is option 'D'. Can you explain this answer?
The differential equation for the equation  is :
is :
a)
b)
c)
d)

|
Sushil Kumar answered |
y = Acos(αx) + Bsin(αx)
dy/dx = -Aαsin(αx) + Bαcos(αx)
d2y/dx2 = -Aα2cos(αx) - Bα2sin(αx)
= -α2(Acos(αx) + Bsin(αx))
= -α2 * y
d2y/dx2 + α2*y = 0
Differential equation representing the family of curves given by y = ax + x2 is:- a)
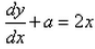
- b)
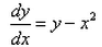
- c)
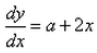
- d)
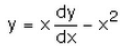
Correct answer is option 'C'. Can you explain this answer?
Differential equation representing the family of curves given by y = ax + x2 is:
a)
b)
c)
d)
|
|
Vikas Kapoor answered |
The answer is C. We eliminate constants.
We have
y=ax+x2
Differentiating with respect to x,
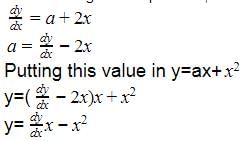
The degree of the differential equation 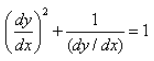
- a)2
- b)1
- c)3
- d)0
Correct answer is option 'C'. Can you explain this answer?
The degree of the differential equation 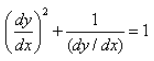
a)
2
b)
1
c)
3
d)
0

|
Sushil Kumar answered |
Given equation is :
(dy/dx)2 + 1/(dy/dx) = 1
((dy/dx)3 + 1)/(dy/dx) = 1
(dy/dx)3 +1 = dy/dx
So, final equation is
(dy/dx)3 - dy/dx + 1 = 0
So, degree = 3
A virtual image, larger than the object can be produced by- a)Convex mirror
- b)Concave mirror
- c)Plane mirror
- d)Concave lens
Correct answer is option 'B'. Can you explain this answer?
A virtual image, larger than the object can be produced by
a)
Convex mirror
b)
Concave mirror
c)
Plane mirror
d)
Concave lens
|
|
Ayaan Madhukar answered |
CONCAVE MIRROR...
Concave mirrors produce real and virtual, erect and inverted, diminished same size and magnified image depending upon the position of the object on the principal axis.
But the concave mirror forms a virtual and enlarged image when the object is placed between the focus and the pole of the mirror...
$$Hope it's help...$$
Concave mirrors produce real and virtual, erect and inverted, diminished same size and magnified image depending upon the position of the object on the principal axis.
But the concave mirror forms a virtual and enlarged image when the object is placed between the focus and the pole of the mirror...
$$Hope it's help...$$
When light is reflected from a mirror a change occurs in its- a)phase,
- b)frequency,
- c)wavelength,
- d)speed
Correct answer is option 'A'. Can you explain this answer?
When light is reflected from a mirror a change occurs in its
a)
phase,
b)
frequency,
c)
wavelength,
d)
speed

|
Ramesh Chand answered |
When a light wave is reflected from an object , it changes not only it's amplitude but also its phase according to the properties of the object at a particular point. Therefore, option A is the right answer.
In image formation from spherical mirrors, only paraxial rays are considered because they- a)are easy to handle geometrically
- b)contain most of the intensity of the incident light
- c)form nearly a point image of a point source
- d)show minimum dispersion effect.
Correct answer is option 'C'. Can you explain this answer?
In image formation from spherical mirrors, only paraxial rays are considered because they
a)
are easy to handle geometrically
b)
contain most of the intensity of the incident light
c)
form nearly a point image of a point source
d)
show minimum dispersion effect.
|
|
Riya Banerjee answered |
Paraxial rays are ones which originate from a point source and make a small angle with the principal axis. After reflection, they give a point image, either real or virtual.
But if rays from point source that are far from the mirror axis, gives a blurred image, an effect called spherical aberration.
But if rays from point source that are far from the mirror axis, gives a blurred image, an effect called spherical aberration.
Two mirrors are placed perpendicular to each other. A ray strikes the first mirror and after reflection from the first mirror it falls on the second mirror. The ray after reflection from second mirror will emerge- a)Perpendicular to the original ray
- b)Parallel to the original ray
- c)At 450 to the original ray
- d)At 600 to the original ray
Correct answer is option 'B'. Can you explain this answer?
Two mirrors are placed perpendicular to each other. A ray strikes the first mirror and after reflection from the first mirror it falls on the second mirror. The ray after reflection from second mirror will emerge
a)
Perpendicular to the original ray
b)
Parallel to the original ray
c)
At 450 to the original ray
d)
At 600 to the original ray
|
|
Preeti Iyer answered |
Let ray strikes the vertical mirror by angle of incidence θ. Then by joining the perpendiculars of two mirrors it is clear from the diagram that angle of incidence at the horizontal mirror is (90−θ).
∴ reflected ray from the horizontal mirror makes angle θ with the horizontal mirror also incident ray at vertical mirror makes angle θ with horizontal axis.
∴ reflected ray is parallel to the original ray.
This is true for two perpendicular mirrors fixed at any positions.

∴ reflected ray from the horizontal mirror makes angle θ with the horizontal mirror also incident ray at vertical mirror makes angle θ with horizontal axis.
∴ reflected ray is parallel to the original ray.
This is true for two perpendicular mirrors fixed at any positions.

If an object is placed unsymmetrically between two plane mirrors, inclined at the angle of 600, then the total number of images formed is- a)5
- b)4
- c)2
- d)infinite
Correct answer is option 'A'. Can you explain this answer?
If an object is placed unsymmetrically between two plane mirrors, inclined at the angle of 600, then the total number of images formed is
a)
5
b)
4
c)
2
d)
infinite
|
|
Hansa Sharma answered |
The number of images between two plane mirror inclined at an angle θ when the object is placed symmetrically between the mirrors is given as
n=(360o/ θ) −1
Given,
θ=60o
∴n=(360o/60)−1=6−1=5
n=(360o/ θ) −1
Given,
θ=60o
∴n=(360o/60)−1=6−1=5
Which of the following letters do not surface lateral inversion- a)HGA
- b)HOX
- c)VET
- d)YUL
Correct answer is option 'B'. Can you explain this answer?
Which of the following letters do not surface lateral inversion
a)
HGA
b)
HOX
c)
VET
d)
YUL
|
|
Hansa Sharma answered |
Lateral inversion-The phenomenon of left side appearing right side and right side appearing left side on reflection in a plane mirror is called lateral inversion.
Letters that do not show lateral inversion are,
A, H, I, M, O, T, U, V, W, X, Y
Hence, HOX will not show lateral inversion.
Letters that do not show lateral inversion are,
A, H, I, M, O, T, U, V, W, X, Y
Hence, HOX will not show lateral inversion.
Formation of the differential equation of the family of curves represented by y = Ae2x + Be-2x is :- a)

- b)
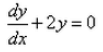
- c)
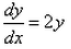
- d)
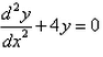
Correct answer is option 'A'. Can you explain this answer?
Formation of the differential equation of the family of curves represented by y = Ae2x + Be-2x is :
a)
b)
c)
d)
|
|
Toushit Lohani answered |
Diiferentiate the eqn twice
y' =2(Ae^2x-Be^2x)
y''=4(Ae^2x+Be^2x)
we get
y''-4y=0
Mark the correct options- a)If the incident rays are converging, we have a real object.
- b)If the final rays are converging, we have a real image.
- c)The image of a virtual object is called a virtual image.
- d)If the image is virtual, the corresponding object is called a virtual object
Correct answer is option 'B'. Can you explain this answer?
Mark the correct options
a)
If the incident rays are converging, we have a real object.
b)
If the final rays are converging, we have a real image.
c)
The image of a virtual object is called a virtual image.
d)
If the image is virtual, the corresponding object is called a virtual object
|
|
Geetika Shah answered |
If the final rays are converging, we have a real image.
This is because a real image is formed by converging reflected/refracted rays from a mirror/lens.
The correct answer is option B.
This is because a real image is formed by converging reflected/refracted rays from a mirror/lens.
The correct answer is option B.
The focal length of spherical mirror is- a)Maximum for red light
- b)Maximum for blue light
- c)Maximum for white light
- d)Same for all lights
Correct answer is option 'D'. Can you explain this answer?
The focal length of spherical mirror is
a)
Maximum for red light
b)
Maximum for blue light
c)
Maximum for white light
d)
Same for all lights
|
|
Lavanya Menon answered |
Focal length is the property of a spherical mirror. It does not depend on the light used. So, it is the same for all lights.
A convex mirror has a focal length f. A real object, placed at a distance f in front of it from the pole, produces an image at- a)2 f
- b)f/2
- c)f
- d)¥
Correct answer is option 'B'. Can you explain this answer?
A convex mirror has a focal length f. A real object, placed at a distance f in front of it from the pole, produces an image at
a)
2 f
b)
f/2
c)
f
d)
¥
|
|
Preeti Iyer answered |
Here F=f
U=-f(-because it is present in front of a convex lens)
It is given that both focal length and object distance is f .
So according to lens formula 1/F=1/v+1/u
So 1/f=(1/v)+(-1/f)
=>1/f=(1/v)-(1/f)
So (1/f)+(1/f)=1/f
=>1+(1/f)=(1/v)
=>2/f=1/v
So from here we can say that v= f/2
Hence option B is correct.
U=-f(-because it is present in front of a convex lens)
It is given that both focal length and object distance is f .
So according to lens formula 1/F=1/v+1/u
So 1/f=(1/v)+(-1/f)
=>1/f=(1/v)-(1/f)
So (1/f)+(1/f)=1/f
=>1+(1/f)=(1/v)
=>2/f=1/v
So from here we can say that v= f/2
Hence option B is correct.
The radius of curvature for a convex lens is 40 cm, for each surface. Its refractive index is 1.5. The focal length will be - a)40 cm
- b)20 cm
- c)80 cm
- d)30 cm
Correct answer is option 'A'. Can you explain this answer?
The radius of curvature for a convex lens is 40 cm, for each surface. Its refractive index is 1.5. The focal length will be
a)
40 cm
b)
20 cm
c)
80 cm
d)
30 cm
|
|
Hansa Sharma answered |
Let the radius of curvature of the convex lens are denoted as
For a convex lens
R1=+40cm [As it is towards right]
R2=-40cm [As it is towards left]
The refractive index of the lens [µ]=1.5
Let f is the focal length of the lens.
From lens maker's formula we know that –
1/f=[µ-1] [1/R1-1/R2]
1/f=[1.5-1][1/40-(1/-40)]
1/f=0.5 x (2/40)
1/f=1/40
f=40cm
Hence, the focal length of the lens is 40 cm.
For a convex lens
R1=+40cm [As it is towards right]
R2=-40cm [As it is towards left]
The refractive index of the lens [µ]=1.5
Let f is the focal length of the lens.
From lens maker's formula we know that –
1/f=[µ-1] [1/R1-1/R2]
1/f=[1.5-1][1/40-(1/-40)]
1/f=0.5 x (2/40)
1/f=1/40
f=40cm
Hence, the focal length of the lens is 40 cm.
An object is placed at a distance u from a concave mirror and its real image is received on a screen placed at a distance of v from the mirror. If f is the focal length of the mirror, then the graph between 1/v versus 1/u is- a)
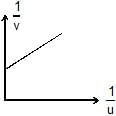
- b)
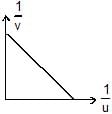
- c)
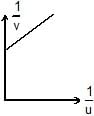
- d)
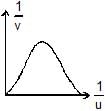
Correct answer is option 'B'. Can you explain this answer?
An object is placed at a distance u from a concave mirror and its real image is received on a screen placed at a distance of v from the mirror. If f is the focal length of the mirror, then the graph between 1/v versus 1/u is
a)
b)
c)
d)

|
Divey Sethi answered |
For real object and real Image,
(1/v)+(1/u)=(1/f)=> -(1/v)-(1/u)=-(1/f)
(1/v)+(1/u)=(1/f) => 1/v=-(1/u)+(1/f)
y=mx+c
The correct answer is option B.
(1/v)+(1/u)=(1/f)=> -(1/v)-(1/u)=-(1/f)
(1/v)+(1/u)=(1/f) => 1/v=-(1/u)+(1/f)
y=mx+c
The correct answer is option B.
An object is initially at a distance of 100 cm from a plane mirror. If the mirror approaches the object at a speed of 5 cm/s. Then after 6 s the distance between the object and its image will be- a)60 cm
- b)140 cm
- c)170 cm
- d)150 cm
Correct answer is option 'B'. Can you explain this answer?
An object is initially at a distance of 100 cm from a plane mirror. If the mirror approaches the object at a speed of 5 cm/s. Then after 6 s the distance between the object and its image will be
a)
60 cm
b)
140 cm
c)
170 cm
d)
150 cm
|
|
Lavanya Menon answered |
Given that,
The distance of object from plane mirror D=100cm
So, initial distance of image and object
=100−(−100)
=200cm
Now, object approaches the mirror with the speed=v=5cm/s
So, distance travelled by object in 6 sec
D=5×6
D=30cm
At this instant,
Distance between mirror and object
D=100−30
D=70cm
Now, the distance between image and object is
D=70−(−70)
D=140cm
Hence, the distance between the object and its image is 140 cm.
The distance of object from plane mirror D=100cm
So, initial distance of image and object
=100−(−100)
=200cm
Now, object approaches the mirror with the speed=v=5cm/s
So, distance travelled by object in 6 sec
D=5×6
D=30cm
At this instant,
Distance between mirror and object
D=100−30
D=70cm
Now, the distance between image and object is
D=70−(−70)
D=140cm
Hence, the distance between the object and its image is 140 cm.
A concave mirror gives an image three times as large as the object placed at a distance of 20 cm from it. For the image to be real, the focal length should be- a)10 cm
- b)15 cm
- c)20 cm
- d)30 cm
Correct answer is option 'B'. Can you explain this answer?
A concave mirror gives an image three times as large as the object placed at a distance of 20 cm from it. For the image to be real, the focal length should be
a)
10 cm
b)
15 cm
c)
20 cm
d)
30 cm
|
|
Hansa Sharma answered |
Given, u=−20cm
m=−3⇒−v/u =−3
v=−60cm
1/f=(1/v)+(1/u)=(-1/60)−(1/20)=−1−3/60
f=−60/4=−15cm
m=−3⇒−v/u =−3
v=−60cm
1/f=(1/v)+(1/u)=(-1/60)−(1/20)=−1−3/60
f=−60/4=−15cm
A concave mirror cannot form- a)virtual image of virtual object
- b)virtual image of a real object
- c)real image of a real object
- d)real image of a virutal object
Correct answer is option 'A'. Can you explain this answer?
A concave mirror cannot form
a)
virtual image of virtual object
b)
virtual image of a real object
c)
real image of a real object
d)
real image of a virutal object
|
|
Ritu Singh answered |
-Virtual image cannot be formed from a virtual object.
- When an object is placed between pole and focus, the image formed by the concave mirror is magnified, virtual and erect.
-When an object is placed beyond the centre of curvature , the image of it is formed between the centre of curvature and focus which is diminished,real and inverted,so the real image of the real object can be formed by a concave mirror.
-When the object is virtual, the image formed is real for the concave surface as shown in figure.
- When an object is placed between pole and focus, the image formed by the concave mirror is magnified, virtual and erect.
-When an object is placed beyond the centre of curvature , the image of it is formed between the centre of curvature and focus which is diminished,real and inverted,so the real image of the real object can be formed by a concave mirror.
-When the object is virtual, the image formed is real for the concave surface as shown in figure.
Formation of the differential equation corresponding to the ellipse major axis 2a and minor axis 2b is:- a)
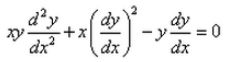
- b)

- c)
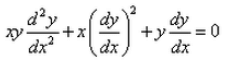
- d)
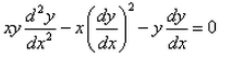
Correct answer is option 'A'. Can you explain this answer?
Formation of the differential equation corresponding to the ellipse major axis 2a and minor axis 2b is:
a)
b)
c)
d)
|
|
Geetika Shah answered |
Equation of ellipse :
x2/a2 + y2/b2 = 1
Differentiation by x,
2x/a2 + (dy/dx)*(2y/b2) = 0
dy/dx = -(b2/a2)(x/y)
-(b2/a^2) = (dy/dx)*(y/x) ----- eqn 1
Again differentiating by x,
d2y/dx2 = -(b2/a2)*((y-x(dy/dx))/y2)
Substituting value of -b2/a2 from eqn 1
d2y/dx2 = (dy/dx)*(y/x)*((y-x(dy/dx))/y2)
d2y/dx2 = (dy/dx)*((y-x*(dy/dx))/xy)
(xy)*(d2y/dx2) = y*(dy/dx) - x*(dy/dx)2
(xy)*(d2y/dx2) + x*(dy/dx)2- y*(dy/dx) = 0
If an object is 30 cm away from a concave mirror of focal length 15 cm, the image will be- a)erect
- b)virtual
- c)diminished
- d)of same size
Correct answer is option 'D'. Can you explain this answer?
If an object is 30 cm away from a concave mirror of focal length 15 cm, the image will be
a)
erect
b)
virtual
c)
diminished
d)
of same size
|
|
Nandita Ahuja answered |
Explanation:
When an object is placed at a distance of 2f (twice the focal length) from a concave mirror, the image formed is of the same size as the object.
In this case, the object is placed at a distance of 30 cm from a concave mirror of focal length 15 cm. So, the distance between the object and the mirror is:
u = -30 cm (since the object is placed in front of the mirror)
f = -15 cm (since the mirror is concave)
Using the mirror formula:
1/f = 1/v + 1/u
1/-15 = 1/v + 1/-30
-2/30 = 1/v
v = -15 cm
So, the image is formed at a distance of 15 cm from the mirror. The magnification is given by:
m = -v/u
m = -15/-30
m = 1/2
Since the magnification is positive, the image formed is erect. And since the magnification is less than 1, the image formed is diminished.
However, since the object is placed at a distance of 2f from the mirror, the image formed is of the same size as the object. Therefore, option D is the correct answer.
When an object is placed at a distance of 2f (twice the focal length) from a concave mirror, the image formed is of the same size as the object.
In this case, the object is placed at a distance of 30 cm from a concave mirror of focal length 15 cm. So, the distance between the object and the mirror is:
u = -30 cm (since the object is placed in front of the mirror)
f = -15 cm (since the mirror is concave)
Using the mirror formula:
1/f = 1/v + 1/u
1/-15 = 1/v + 1/-30
-2/30 = 1/v
v = -15 cm
So, the image is formed at a distance of 15 cm from the mirror. The magnification is given by:
m = -v/u
m = -15/-30
m = 1/2
Since the magnification is positive, the image formed is erect. And since the magnification is less than 1, the image formed is diminished.
However, since the object is placed at a distance of 2f from the mirror, the image formed is of the same size as the object. Therefore, option D is the correct answer.
A person is in a room whose ceiling and two adjacent walls are mirrors. How many images are formed ?- a)5
- b)6
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
A person is in a room whose ceiling and two adjacent walls are mirrors. How many images are formed ?
a)
5
b)
6
c)
7
d)
8
|
|
Geetika Shah answered |
The number of images formed when two mirrors are inclined to each other is given by :
n=(360/θ -1)
here θ= 90°[since walls are perpendicular]
so, number of images=n=360/90-1
=4-1
=3
These 3 images are formed by a combination of two adjacent walls with the object itself acts as objects for the ceiling mirror. So totally 4 images are formed.
Hence total number of images formed are 4+3= 7
n=(360/θ -1)
here θ= 90°[since walls are perpendicular]
so, number of images=n=360/90-1
=4-1
=3
These 3 images are formed by a combination of two adjacent walls with the object itself acts as objects for the ceiling mirror. So totally 4 images are formed.
Hence total number of images formed are 4+3= 7
A rays is incident at an angle 38º on a mirror. The angle between normal and reflected ray is- a)38º
- b)52º
- c)90º
- d)76º
Correct answer is option 'A'. Can you explain this answer?
A rays is incident at an angle 38º on a mirror. The angle between normal and reflected ray is
a)
38º
b)
52º
c)
90º
d)
76º
|
|
Kalyan Joshi answered |
As per the question, rays are falling on the mirror, which cleared that Regular reflection is taking place.
So, As per the laws of regular reflection.
=> ∠incident= ∠reflection
∠incident= ∠reflection=38Ao
Also we know that normal is at 90°to the mirror.
Now, to get the required angle we need to reduce angle of reflection from normal.
=>90Ao-38Ao=52Ao
so, the correct answer is option B.
So, As per the laws of regular reflection.
=> ∠incident= ∠reflection
∠incident= ∠reflection=38Ao
Also we know that normal is at 90°to the mirror.
Now, to get the required angle we need to reduce angle of reflection from normal.
=>90Ao-38Ao=52Ao
so, the correct answer is option B.
A point object is kept in front of a plane mirror. The plane mirror is doing SHM of amplitude 2cm. The plane mirror moves along the x-axis and x-axis is normal to the mirror. The amplitude of the mirror is such that the object is always infront of the mirror. The amplitude of SHM of the image is- a)zero
- b)2 cm
- c)4 cm
- d)1 cm
Correct answer is option 'C'. Can you explain this answer?
A point object is kept in front of a plane mirror. The plane mirror is doing SHM of amplitude 2cm. The plane mirror moves along the x-axis and x-axis is normal to the mirror. The amplitude of the mirror is such that the object is always infront of the mirror. The amplitude of SHM of the image is
a)
zero
b)
2 cm
c)
4 cm
d)
1 cm
|
|
Jayant Mishra answered |
The answer is 4cm.
In reflection on a plane mirror the image distance is equal to the object distance.
The size of the image equals to the size of the object.
Therefore the size of the amplitude of the reflected amplitude equals the size of the original amplitude.
A particle is moving towards a fixed spherical mirror. The image :- a)Must move away from the mirror
- b)Must move towards the mirror.
- c)May move towards the mirror.
- d)Will move towards the mirror, only if the mirror is convex.
Correct answer is option 'D'. Can you explain this answer?
A particle is moving towards a fixed spherical mirror. The image :
a)
Must move away from the mirror
b)
Must move towards the mirror.
c)
May move towards the mirror.
d)
Will move towards the mirror, only if the mirror is convex.
|
|
Rajat Kapoor answered |
If the mirror is concave and a real object is approaching it, the image will move away from the mirror for object distance greater than focal length. If object distance is less than the focal length, virtual image will be formed which moves towards the mirror. If mirror is convex, as object is approaching the mirror, image will move from focus to pole ie, towards the mirror.
The images of clouds and trees in water always less bright than in reality- a)because water is forming the image dirty
- b)because there is an optical illusion due to which the image appears to be less bright
- c)because only a portion of the incident light is reflected and quite a large portion goes mid water
- d)because air above the surface of water contains a lot of moisture
Correct answer is option 'C'. Can you explain this answer?
The images of clouds and trees in water always less bright than in reality
a)
because water is forming the image dirty
b)
because there is an optical illusion due to which the image appears to be less bright
c)
because only a portion of the incident light is reflected and quite a large portion goes mid water
d)
because air above the surface of water contains a lot of moisture
|
|
Rishika Patel answered |
The images of clouds and trees in water are always less bright than in reality because only a portion of the incident light is reflected and quite a large portion goes mid water.
If a ray of light is incident on a plane mirror at an angle 60° from the mirror surface, then deviation produced by mirror is- a)30°
- b)60°
- c)90°
- d)120°
Correct answer is option 'D'. Can you explain this answer?
If a ray of light is incident on a plane mirror at an angle 60° from the mirror surface, then deviation produced by mirror is
a)
30°
b)
60°
c)
90°
d)
120°
|
|
Anisha Bose answered |
The angle of incidence is the angle between the incident ray and the normal to the mirror at the point of incidence. In this case, the angle of incidence is 60 degrees.
The angle of reflection is the angle between the reflected ray and the normal to the mirror at the point of incidence. According to the law of reflection, this angle is equal to the angle of incidence. Therefore, the angle of reflection in this case is also 60 degrees.
The normal to the mirror is a line perpendicular to the surface of the mirror at the point of incidence. If the incident ray is coming from the left side of the mirror and making an angle of 60 degrees with the normal, then the reflected ray will be on the right side of the mirror and also make an angle of 60 degrees with the normal.
The incident ray, the reflected ray, and the normal all lie in the same plane, which is the plane of the mirror. This is also true for any other incident ray that makes an angle of 60 degrees with the normal at the point of incidence.
The image of an object formed by a plane mirror is virtual, upright, and the same size as the object. The image is located behind the mirror and is at the same distance from the mirror as the object is in front of the mirror. In this case, the image will be located at a distance of 2 times the distance of the object from the mirror.
The angle of reflection is the angle between the reflected ray and the normal to the mirror at the point of incidence. According to the law of reflection, this angle is equal to the angle of incidence. Therefore, the angle of reflection in this case is also 60 degrees.
The normal to the mirror is a line perpendicular to the surface of the mirror at the point of incidence. If the incident ray is coming from the left side of the mirror and making an angle of 60 degrees with the normal, then the reflected ray will be on the right side of the mirror and also make an angle of 60 degrees with the normal.
The incident ray, the reflected ray, and the normal all lie in the same plane, which is the plane of the mirror. This is also true for any other incident ray that makes an angle of 60 degrees with the normal at the point of incidence.
The image of an object formed by a plane mirror is virtual, upright, and the same size as the object. The image is located behind the mirror and is at the same distance from the mirror as the object is in front of the mirror. In this case, the image will be located at a distance of 2 times the distance of the object from the mirror.
A straight line joining the object point and image point is always perpendicular to the mirror- a) If mirror is plane only
- b) If mirror is concave only
- c)If mirror is convex only
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
A straight line joining the object point and image point is always perpendicular to the mirror
a)
If mirror is plane only
b)
If mirror is concave only
c)
If mirror is convex only
d)
None of these
|
|
Shreya Gupta answered |
A straight line joining the object point and image point is always perpendicular to the mirror because it passes through the centre of curvature in spherical mirrors. And in case of plane mirrors they bisects the line between the object and the image.
A concave mirror of radius of curvature 20 cm forms image of the sun. The diameter of the sun subtends an angle 1° on the earth. Then the diameter of the image is (in cm)- a)2π/9
- b)π/9
- c)20
- d)π/18
Correct answer is option 'D'. Can you explain this answer?
A concave mirror of radius of curvature 20 cm forms image of the sun. The diameter of the sun subtends an angle 1° on the earth. Then the diameter of the image is (in cm)
a)
2π/9
b)
π/9
c)
20
d)
π/18
|
|
Madhurima Mishra answered |
Given: A concave mirror of radius of curvature 20cm forms image of the sun. The diameter of the sun subtends an angle 1o on the earth.
To find the diameter of the image
Solution:
As sun is more far from the earth,
Then we take u = infinite
Radius of curvature, R=−20cm
Focal length,
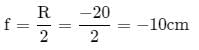
From the mirror formula

d = π/18
A point source of light is placed in front of a plane mirror.- a)Only the reflected rays close to the normal meet at a point when produced backward
- b)All the reflected rays meet at a point when produced backward
- c)Only the reflected rays making a small angle with the mirror, meet at a point when produced backward
- d)Light of different colours make different images
Correct answer is option 'B'. Can you explain this answer?
A point source of light is placed in front of a plane mirror.
a)
Only the reflected rays close to the normal meet at a point when produced backward
b)
All the reflected rays meet at a point when produced backward
c)
Only the reflected rays making a small angle with the mirror, meet at a point when produced backward
d)
Light of different colours make different images
|
|
Nisha Pillai answered |
Plane mirror always forms a virtual image of the real object for all the rays emitted by the object. So, when a point source of light is placed in front of a plane mirror, all the reflected rays meet at a point when produced backward.
Option B is correct.
Option B is correct.
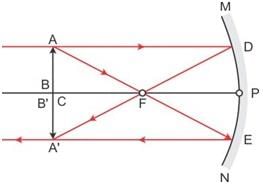
In case of concave mirror, the minimum distance between a real object and its real image is :- a)f
- b)2f
- c)4f
- d)Zero
Correct answer is option 'D'. Can you explain this answer?
In case of concave mirror, the minimum distance between a real object and its real image is :
a)
f
b)
2f
c)
4f
d)
Zero
|
|
Shreya Gupta answered |
The minimum distance between an object and its real image in the case of a concave mirror is Zero.
When the object is at the 2F distance i.e. the center of curvature, then the image is real and formed inverted at the same distance.

An infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is at a distance u > f from the mirror. Its image will have a length- a)f2/(u _ f)
- b)uf/(u _ f)
- c)f2/(u + f)
- d)uf /(u + f)
Correct answer is option 'A'. Can you explain this answer?
An infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is at a distance u > f from the mirror. Its image will have a length
a)
f2/(u _ f)
b)
uf/(u _ f)
c)
f2/(u + f)
d)
uf /(u + f)
|
|
Jyoti Kapoor answered |
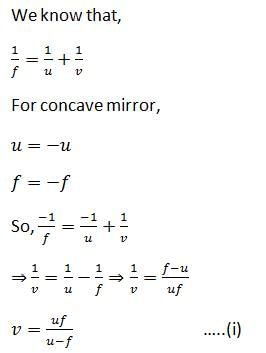
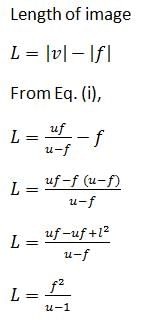
The order and degree of the differential equation: (y”)2 + (y”)3 + (y’)4 + y5 = 0 is:- a)2, 4
- b)3, 5
- c)2, 5
- d)2, 3
Correct answer is option 'D'. Can you explain this answer?
The order and degree of the differential equation: (y”)2 + (y”)3 + (y’)4 + y5 = 0 is:
a)
2, 4
b)
3, 5
c)
2, 5
d)
2, 3
|
|
Naina Bansal answered |
Toolbox:
The highest order derivative present in the differential equation determines its order.
The highest power raise to the derivative determines its degree.
(y′′′)^2+(y′′)^3+(y′)^4+y^5 = 0
The order of the given equation is 3.
The degree corresponding to the highest order is 2
The order of the differential equation: 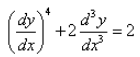
- a)4
- b)2
- c)3
- d)1
Correct answer is option 'C'. Can you explain this answer?
The order of the differential equation: 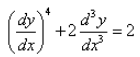
a)
4
b)
2
c)
3
d)
1

|
Anuj Seth answered |
Order is seen from highest efficiency of differentiability I.e. in hindi , kisi bhi equation me jisme sabse jyada differential power hai wo jeeta
The largest distance of the image of a real object from a convex mirror of focal length 20 cm can be- a)20 cm
- b)infinite
- c)10 cm
- d)depends on the position of the object
Correct answer is option 'C'. Can you explain this answer?
The largest distance of the image of a real object from a convex mirror of focal length 20 cm can be
a)
20 cm
b)
infinite
c)
10 cm
d)
depends on the position of the object
|
|
Rutuja Ahuja answered |
We are given that:
Focal length = 20 cm
In a convex mirror image is formed between focal length and mirror.
So the maximum distance is f i.e. focal length of the mirror.
Now
f = 20 / 2 = 10 cm
Thus the largest distance of an image from a convex mirror is 10 cm.
Focal length = 20 cm
In a convex mirror image is formed between focal length and mirror.
So the maximum distance is f i.e. focal length of the mirror.
Now
f = 20 / 2 = 10 cm
Thus the largest distance of an image from a convex mirror is 10 cm.
A watch shows the time as 3 : 25. What will be the time that appears when seen through a plane mirror ?- a)8 : 35
- b)9 : 35
- c)7 : 35
- d)8 : 25
Correct answer is option 'A'. Can you explain this answer?
A watch shows the time as 3 : 25. What will be the time that appears when seen through a plane mirror ?
a)
8 : 35
b)
9 : 35
c)
7 : 35
d)
8 : 25
|
|
Upasana Sen answered |
The relation between actual time and given time is:
Actual time=11:60 −given time
Actual time=11:60−3:25=8:35
Actual time=11:60 −given time
Actual time=11:60−3:25=8:35
A point source of light is placed in front of a plane mirror.- a)All the reflected rays meet at a point when produced backward.
- b)Only the reflected rays close to the normal meet at a point when produced backward.
- c)Only the reflected rays making a small angle with the mirror, meet at a point when produced backward
- d)Light of different colours make different images.
Correct answer is option 'A'. Can you explain this answer?
A point source of light is placed in front of a plane mirror.
a)
All the reflected rays meet at a point when produced backward.
b)
Only the reflected rays close to the normal meet at a point when produced backward.
c)
Only the reflected rays making a small angle with the mirror, meet at a point when produced backward
d)
Light of different colours make different images.
|
|
Navya Banerjee answered |
Plane mirror always forms a virtual image of the real object for all the rays emitted by the object. So, when a point source of light is placed in front of a plane mirror, all the reflected rays meet at a point when produced backward.
Option A is correct.
Option A is correct.
Chapter doubts & questions for December Week 3 - Weekly Tests for JEE Preparation 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of December Week 3 - Weekly Tests for JEE Preparation in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily












