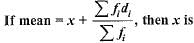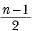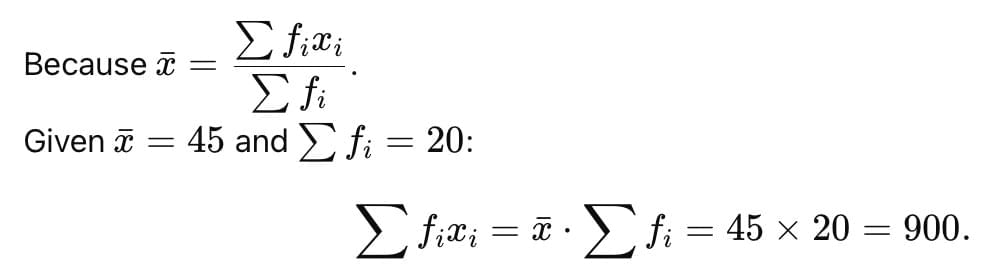All Exams >
Class 10 >
Mathematics Class 10 (Maharashtra SSC Board) >
All Questions
All questions of Statistics for Class 10 Exam
Find out the mode of the following data:
- a)450
- b)400
- c)600
- d)478
Correct answer is option 'A'. Can you explain this answer?
Find out the mode of the following data:
a)
450
b)
400
c)
600
d)
478
|
Rohini Seth answered |
The mode of a set of data values is the value that appears most often .So mode is the most occurrence of observation.
Converting the distribution in continuous grouped and applying the formula
Mode=
Modal class is 400-500
Where L=lower limit of the modal class =400
f1= modal class frequency=32
f2 = just after the modal class frequency=20
f0 = just previous the modal class frequency=20
C = Class size=100
Mode=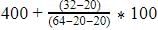
=400+50=450
Converting the distribution in continuous grouped and applying the formula
Mode=
Modal class is 400-500
Where L=lower limit of the modal class =400
f1= modal class frequency=32
f2 = just after the modal class frequency=20
f0 = just previous the modal class frequency=20
C = Class size=100
Mode=
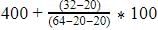
=400+50=450
The mean of 1, 2, 3, 4 …n is given by- a)
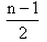
- b)n/2
- c)
- d)
Correct answer is option 'D'. Can you explain this answer?
The mean of 1, 2, 3, 4 …n is given by
a)
b)
n/2
c)
d)
|
Krishna Iyer answered |
⇒ We have the sequence, 1,2,3.......n
⇒ This is an AP, with the initial term a=1 and the common difference d=1.
∴ The sum of n terms of an AP is given by,
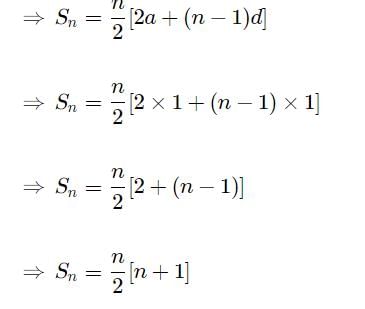
→ Arithmetic mean of n numbers a1,a2,a3,a4,...an is given by the formula
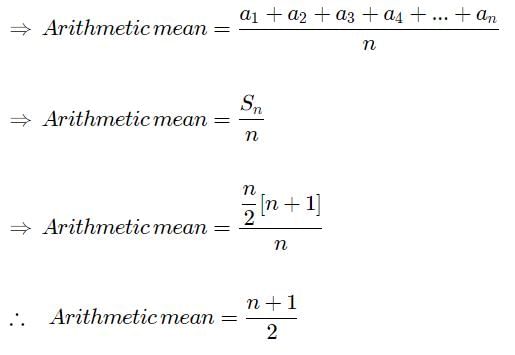
⇒ This is an AP, with the initial term a=1 and the common difference d=1.
∴ The sum of n terms of an AP is given by,
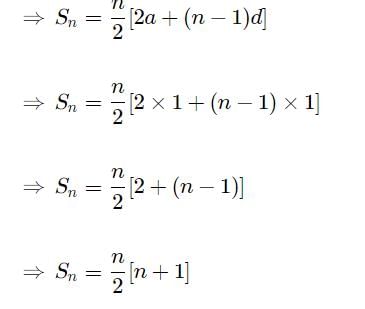
→ Arithmetic mean of n numbers a1,a2,a3,a4,...an is given by the formula
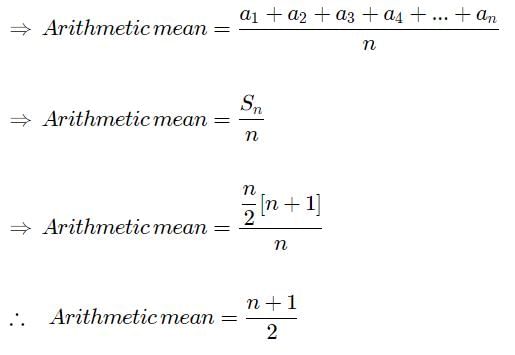
What is the mode of the given data?- a)24
- b)21
- c)22
- d)25
Correct answer is option 'A'. Can you explain this answer?
What is the mode of the given data?
a)
24
b)
21
c)
22
d)
25
|
Skyhigh Academy answered |
Mode=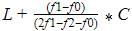 
Where L=lower limit of the modal class =20
f1= modal class frequency.=27
f2 = just after the modal class frequency.=21
f0 = just previous the modal class frequency=23
C = Class size=10
Mode=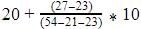
=20+4=24
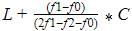
Where L=lower limit of the modal class =20
f1= modal class frequency.=27
f2 = just after the modal class frequency.=21
f0 = just previous the modal class frequency=23
C = Class size=10
Mode=
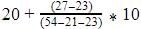
=20+4=24
If mean = (3 median - mode). k, then the value of k is- a)1
- b)2
- c)1/2
- d)3/2
Correct answer is option 'C'. Can you explain this answer?
If mean = (3 median - mode). k, then the value of k is
a)
1
b)
2
c)
1/2
d)
3/2
|
|
Kiran Mehta answered |
∵ Mode = 3 median - 2 mean
⇒ 2 mean = 3 m edian - mode
⇒ 2 mean = 3 m edian - mode
The age of 18 students of a class is reported below. Their modal age is 10, 17, 14, 10, 11, 12, 12, 13, 17, 13, 14, 14, 15, 16, 17, 15, 17, 16- a)22 years
- b)17 years
- c)14 years
- d)16 years
Correct answer is option 'B'. Can you explain this answer?
The age of 18 students of a class is reported below. Their modal age is 10, 17, 14, 10, 11, 12, 12, 13, 17, 13, 14, 14, 15, 16, 17, 15, 17, 16
a)
22 years
b)
17 years
c)
14 years
d)
16 years
|
Gaurav Kumar answered |
Mode is the highest number of times an observation occurs, which means the number that appears most frequently in a set. So modal age is the age which occurs maximum number of times. It is evident that 17 occurs most of the times. So, modal age is 17 years.
The mean of 15 numbers is 25. If each number is multiplied by 4, mean of the new numbers is- a)100
- b)40
- c)10
- d)60
Correct answer is option 'A'. Can you explain this answer?
The mean of 15 numbers is 25. If each number is multiplied by 4, mean of the new numbers is
a)
100
b)
40
c)
10
d)
60
|
Anmol Das answered |
Answer:
100
Step-by-step explanation:
mean=25
every number is multiplied by 4,
then 4 is common
Therefore, 25x4=100
The mean of five numbers is 28. If one of the numbers is excluded, the mean gets reduced by 2. The excluded number is- a)45
- b)36
- c)30
- d)25
Correct answer is option 'B'. Can you explain this answer?
The mean of five numbers is 28. If one of the numbers is excluded, the mean gets reduced by 2. The excluded number is
a)
45
b)
36
c)
30
d)
25
|
Vikas Kumar answered |
Mean of 5 nos.= 28
Therefore, sum of the 5 nos. = 28 * 5 = 140
The the no. exclude by 'x'.
New sum of 4 nos.= 140 - x
New mean = 28- 2 = 26
Therefore, (140 - x ) / 4 = 26
=> 140 - x = 104
=> x = 36
ANSWER= 36
The mean of the following data is: 45, 35, 20, 15, 25, 40- a)15
- b)25
- c)30
- d)35
Correct answer is option 'C'. Can you explain this answer?
The mean of the following data is: 45, 35, 20, 15, 25, 40
a)
15
b)
25
c)
30
d)
35
|
Pankaj verma answered |
Mean of Data Set
To find the mean of a data set, we add up all the numbers in the set and then divide by the total number of values in the set.
Calculation
To find the mean of the given data set, we need to add up all the numbers in the set and then divide by the total number of values in the set:
Mean = (45 + 35 + 20 + 15 + 25 + 40) / 6
Mean = 180 / 6
Mean = 30
Therefore, the mean of the given data set is 30. The correct answer is option C.
To find the mean of a data set, we add up all the numbers in the set and then divide by the total number of values in the set.
Calculation
To find the mean of the given data set, we need to add up all the numbers in the set and then divide by the total number of values in the set:
Mean = (45 + 35 + 20 + 15 + 25 + 40) / 6
Mean = 180 / 6
Mean = 30
Therefore, the mean of the given data set is 30. The correct answer is option C.
Mode is not affected by- a)Maximum value
- b)Minimum value
- c)Extreme values
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Mode is not affected by
a)
Maximum value
b)
Minimum value
c)
Extreme values
d)
All of the above
|
Hitesh naidu answered |
Understanding Mode and Its Characteristics
The mode is a statistical measure that represents the value that appears most frequently in a data set. It plays a crucial role in descriptive statistics and is particularly useful when analyzing categorical data.
Why Mode is Not Affected by Extreme Values
- Maximum Value: The maximum value in a data set refers to the highest number. If this number appears only once, it does not influence the mode, which is determined by frequency rather than magnitude.
- Minimum Value: Similar to the maximum, the minimum value or the lowest number in a data set can exist without affecting the mode. If the minimum is unique or infrequent, it will not change the mode.
- Extreme Values: Extreme values (outliers) are data points that differ significantly from other observations. While these values can impact measures like mean or median, they do not affect the mode as long as the most frequent value remains unchanged.
Conclusion
In summary, the mode remains stable despite changes in maximum or minimum values, or the presence of extreme values. It solely relies on the frequency of occurrence in the data set. Thus, the correct answer is option 'D', indicating that the mode is not influenced by maximum, minimum, or extreme values.
The mode is a statistical measure that represents the value that appears most frequently in a data set. It plays a crucial role in descriptive statistics and is particularly useful when analyzing categorical data.
Why Mode is Not Affected by Extreme Values
- Maximum Value: The maximum value in a data set refers to the highest number. If this number appears only once, it does not influence the mode, which is determined by frequency rather than magnitude.
- Minimum Value: Similar to the maximum, the minimum value or the lowest number in a data set can exist without affecting the mode. If the minimum is unique or infrequent, it will not change the mode.
- Extreme Values: Extreme values (outliers) are data points that differ significantly from other observations. While these values can impact measures like mean or median, they do not affect the mode as long as the most frequent value remains unchanged.
Conclusion
In summary, the mode remains stable despite changes in maximum or minimum values, or the presence of extreme values. It solely relies on the frequency of occurrence in the data set. Thus, the correct answer is option 'D', indicating that the mode is not influenced by maximum, minimum, or extreme values.
The mean of a data set with 12 observations is calculated as 19.25. If one more value is included in the data, then for the new data with 13 observations, mean becomes 20. Value of this 13th observation is- a)28
- b)29
- c)31
- d)30
Correct answer is option 'B'. Can you explain this answer?
The mean of a data set with 12 observations is calculated as 19.25. If one more value is included in the data, then for the new data with 13 observations, mean becomes 20. Value of this 13th observation is
a)
28
b)
29
c)
31
d)
30
|
Anita Menon answered |
Suppose be all twelevth terms = x
Mean = Terms / Observation
19 . 25 = x / 12
x = 19.25 × 12
x = 231 .00
Now let thirteenth term will be y
Mean = 20
So, 20 = x + y / 13
20 = 231 + y / 13
20 × 13 = 231 + x
260 = 231 + x
260 - 231 = x
29 = x
Mean = Terms / Observation
19 . 25 = x / 12
x = 19.25 × 12
x = 231 .00
Now let thirteenth term will be y
Mean = 20
So, 20 = x + y / 13
20 = 231 + y / 13
20 × 13 = 231 + x
260 = 231 + x
260 - 231 = x
29 = x
The class mark of the class 15.5 - 20.5
- a)15.5
- b)20.5
- c)18
- d)5
Correct answer is option 'C'. Can you explain this answer?
The class mark of the class 15.5 - 20.5
a)
15.5
b)
20.5
c)
18
d)
5
|
Crafty Classes answered |
class mark= (upper limit+lower limit)/2
= (15.5+20.5)/2
=36/2
=18
= (15.5+20.5)/2
=36/2
=18
The lower limit of the modal class of the following data is:
- a)10
- b)20
- c)30
- d)50
Correct answer is option 'B'. Can you explain this answer?
The lower limit of the modal class of the following data is:
a)
10
b)
20
c)
30
d)
50
|
|
Raghav Bansal answered |
Modal class is the interval which has the highest frequency ie, which occur most of the times.Here highest frequency is 13 in the class interval 20-30. So lower limit of the class interval is 20.
Mode and mean of a data are 12k and 15k. Median of the data is- a)12k
- b)14k
- c)15k
- d)16k
Correct answer is option 'B'. Can you explain this answer?
Mode and mean of a data are 12k and 15k. Median of the data is
a)
12k
b)
14k
c)
15k
d)
16k
|
|
Amit Kumar answered |
Here's the solution to your question:
If two values are given in the below formula than we can use the formula if one is given than we cannot use the formula
3median = 2mean+mode
3median = 2(15k)+12k
3median = 30k+12k
3median = 42k
median = 42k/3
median = 14k
You can understand all the concepts of Class 10 mathematics through the link:
The class marks of the class 18-22 is- a)4
- b)18
- c)22
- d)20
Correct answer is option 'D'. Can you explain this answer?
The class marks of the class 18-22 is
a)
4
b)
18
c)
22
d)
20
|
|
Harshit Agrawal answered |
We know that ,
Class Mark = upper limit + lower limit /2
--->. Class Mark = 22 + 18/2
--->. Class Mark = 40/2
--->. Class Mark = 20
Hence , option D is correct.
Class Mark = upper limit + lower limit /2
--->. Class Mark = 22 + 18/2
--->. Class Mark = 40/2
--->. Class Mark = 20
Hence , option D is correct.
The mean of first ten even natural numbers is- a)100
- b)11
- c)30
- d)10
Correct answer is option 'B'. Can you explain this answer?
The mean of first ten even natural numbers is
a)
100
b)
11
c)
30
d)
10
|
|
Anmol Das answered |
Mean of First Ten Even Natural Numbers
To find the mean of the first ten even natural numbers, we need to add all the even numbers and divide the sum by the total number of even numbers. The first ten even natural numbers are:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20
1. Add up the Even Numbers
Add up all the even numbers:
2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 = 110
2. Divide the Sum by the Total Number of Even Numbers
Since there are 10 even numbers in the list, we divide the sum by 10:
110 ÷ 10 = 11
Therefore, the mean of the first ten even natural numbers is 11. Option 'B' is the correct answer.
To find the mean of the first ten even natural numbers, we need to add all the even numbers and divide the sum by the total number of even numbers. The first ten even natural numbers are:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20
1. Add up the Even Numbers
Add up all the even numbers:
2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 = 110
2. Divide the Sum by the Total Number of Even Numbers
Since there are 10 even numbers in the list, we divide the sum by 10:
110 ÷ 10 = 11
Therefore, the mean of the first ten even natural numbers is 11. Option 'B' is the correct answer.
Mean of 100 items is 49. It was discovered that three items which should have been 60, 70, 80 were wrongly read as 40, 20, 50 respectively. The correct mean is- a)48
- b)49
- c)50
- d)60
Correct answer is option 'C'. Can you explain this answer?
Mean of 100 items is 49. It was discovered that three items which should have been 60, 70, 80 were wrongly read as 40, 20, 50 respectively. The correct mean is
a)
48
b)
49
c)
50
d)
60
|
|
Ananya Das answered |
Sum of 100 observations = 100 x 49 = 4900
Correct sum = 4900 - [40 + 20 + 50] + [60 + 70 + 80] = 5000
∴ Correct mean = 5000/100 = 50
Correct sum = 4900 - [40 + 20 + 50] + [60 + 70 + 80] = 5000
∴ Correct mean = 5000/100 = 50
The modal class in the following frequency distribution is: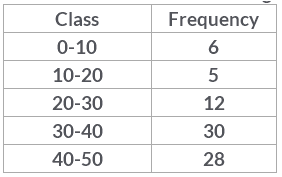 
- a)40-50
- b)30-40
- c)20-30
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The modal class in the following frequency distribution is:
a)
40-50
b)
30-40
c)
20-30
d)
None of these
|
|
Raghav Bansal answered |
The modal class is the class with the highest frequency ie, the class which occurs the most. So,30-40 has frequency 30 which is the highest, therefore, 30-40 is the modal class.
The mean of 5 observations x, x + 2, x + 4, x + 6 and x + 8 is 11, then the value of x is:- a)6
- b)4
- c)7
- d)11
Correct answer is option 'C'. Can you explain this answer?
The mean of 5 observations x, x + 2, x + 4, x + 6 and x + 8 is 11, then the value of x is:
a)
6
b)
4
c)
7
d)
11
|
|
Krishna Iyer answered |
(x + x + 2 + x + 4 + x + 6 + x + 8) / 5 = 11
5x + 20 = 55
5x = 35 ⇒ x = 7
5x + 20 = 55
5x = 35 ⇒ x = 7
The graphical representation of a cumulative frequency distribution is called- a)Bar graph
- b)Histogram
- c)Frequency polygon
- d)Ogive
Correct answer is option 'D'. Can you explain this answer?
The graphical representation of a cumulative frequency distribution is called
a)
Bar graph
b)
Histogram
c)
Frequency polygon
d)
Ogive
|
|
Anjana Khatri answered |
The graphical representation of a cumulative frequency distribution is called an ogive.
An ogive is a graph that plots the cumulative frequency of a set of data on the y-axis and the data values on the x-axis. It is used to represent the distribution of continuous data and is shaped like a curve.
A frequency polygon is also a graph that represents the frequency distribution of a set of data, but it is shaped like a polygon with straight lines connecting the data points. A bar graph is a graph that uses bars to represent the frequencies or counts of a set of data, and a histogram is a graph that represents the frequency distribution of continuous data using bars.
Construction of a cumulative frequency table is useful in determining the- a)mean
- b)median
- c)mode
- d)all of the above
Correct answer is option 'B'. Can you explain this answer?
Construction of a cumulative frequency table is useful in determining the
a)
mean
b)
median
c)
mode
d)
all of the above
|
Girish mehra answered |
The correct answer is b
A cumulative frequency table helps to determine the median of the series.
In the formula, Mode 
- a)frequency of the modal class
- b)frequency of the second class
- c)frequency of the class preceding the modal class
- d)frequency of the class succeeding the modal class
Correct answer is option 'D'. Can you explain this answer?
In the formula, Mode
a)
frequency of the modal class
b)
frequency of the second class
c)
frequency of the class preceding the modal class
d)
frequency of the class succeeding the modal class
|
|
Crafty Classes answered |
The formula to find the mode of the grouped data is: Mode = l + [(f1-f0)/(2f1-f0-f2)]×h. Where, l = lower class limit of modal class, h = class size, f1 = frequency of modal class, f0 = frequency of class proceeding to modal class, f2 = frequency of class succeeding to modal class.
Modal age of students in given distribution is- a)14 years
- b)12 years
- c)13 years
- d)15 years
Correct answer is option 'C'. Can you explain this answer?
Modal age of students in given distribution is
a)
14 years
b)
12 years
c)
13 years
d)
15 years
|
|
Amit Sharma answered |
Mode is the most frequently occurring observation. Since it's not a grouped data the frequency is the occurrence of only one observation , So the highest no. of frequency is 7 . So the modal age is 13.
While computing mean of a grouped data, we assume that the frequencies are- a)centered at the lower limits of the classes
- b)centered at the upper limits of the classes
- c)centered at the class marks of the classes
- d)evenly distributed over all the classes
Correct answer is option 'C'. Can you explain this answer?
While computing mean of a grouped data, we assume that the frequencies are
a)
centered at the lower limits of the classes
b)
centered at the upper limits of the classes
c)
centered at the class marks of the classes
d)
evenly distributed over all the classes
|
Kds Coaching answered |
- When computing the mean of grouped data, we assume that the frequencies are centered at the class marks of the classes.
- This means that each frequency is associated with the midpoint of its respective class interval.
- Using the class marks allows for an accurate calculation of the mean by multiplying each class mark by its frequency, summing these products, and then dividing by the total frequency.
The mode of 12, 17, 16, 14, 13, 16, 11, 14 is- a)13
- b)11
- c)14
- d)14 and 16
Correct answer is option 'D'. Can you explain this answer?
The mode of 12, 17, 16, 14, 13, 16, 11, 14 is
a)
13
b)
11
c)
14
d)
14 and 16
|
Sahana dasgupta answered |
To find the mode of a set of numbers, we need to determine the number(s) that appear most frequently in the set. In this case, the set of numbers is 12, 17, 16, 14, 13, 16, 11, and 14.
**Step 1: Arrange the numbers in ascending order:**
11, 12, 13, 14, 14, 16, 16, 17
**Step 2: Count the frequency of each number:**
11 appears once
12 appears once
13 appears once
14 appears twice
16 appears twice
17 appears once
**Step 3: Determine the number(s) with the highest frequency:**
In this case, the numbers 14 and 16 appear most frequently, each occurring twice. Therefore, the mode of the set is 14 and 16.
However, the options provided are a)13, b)11, c)14, and d)14 and 16. The correct answer is option d)14 and 16 because both numbers have the highest frequency in the set.
Therefore, the mode of the given set of numbers 12, 17, 16, 14, 13, 16, 11, and 14 is 14 and 16.
**Step 1: Arrange the numbers in ascending order:**
11, 12, 13, 14, 14, 16, 16, 17
**Step 2: Count the frequency of each number:**
11 appears once
12 appears once
13 appears once
14 appears twice
16 appears twice
17 appears once
**Step 3: Determine the number(s) with the highest frequency:**
In this case, the numbers 14 and 16 appear most frequently, each occurring twice. Therefore, the mode of the set is 14 and 16.
However, the options provided are a)13, b)11, c)14, and d)14 and 16. The correct answer is option d)14 and 16 because both numbers have the highest frequency in the set.
Therefore, the mode of the given set of numbers 12, 17, 16, 14, 13, 16, 11, and 14 is 14 and 16.
For the following distribution the modal class is
- a)30-40
- b)40-50
- c)20-30
- d)10-20
Correct answer is option 'B'. Can you explain this answer?
For the following distribution the modal class is
a)
30-40
b)
40-50
c)
20-30
d)
10-20
|
EduRev Class 10 answered |
To find the modal class from a given frequency distribution, we look for the class interval with the highest frequency. The class interval with the highest frequency is referred to as the modal class.
In the provided distribution, we have cumulative frequencies, so we need to first determine the frequency of each class interval. To do this, we subtract the cumulative frequency of the preceding class from the cumulative frequency of the current class.
Here are the cumulative frequencies provided for each class:
- Marks below 10: 2 students
- Marks below 20: 11 students
- Marks below 30: 25 students
- Marks below 40: 45 students
- Marks below 50: 67 students
- Marks below 60: 75 students
Now let's calculate the frequency for each class interval:
- 10-20: 11−2=911−2=9
- 20-30: 25−11=1425−11=14
- 30-40: 45−25=2045−25=20
- 40-50: 67−45=2267−45=22
- 50-60: 75−67=875−67=8
The class interval with the highest frequency is 40-50 with 22 students, making it the modal class. Therefore, the correct answer is option 2: 40-50.
The mean of a data set with 12 observations is calculated as 19.25. If one more value is included in the data, then for the new data with 13 observations, mean becomes 20. The value of this 13th observation is- a)28
- b)29
- c)30
- d)31
Correct answer is option 'B'. Can you explain this answer?
The mean of a data set with 12 observations is calculated as 19.25. If one more value is included in the data, then for the new data with 13 observations, mean becomes 20. The value of this 13th observation is
a)
28
b)
29
c)
30
d)
31
|
|
Hitesh naidu answered |
Given: Mean of a data set with 12 observations = 19.25
Mean of the new data set with 13 observations = 20
To find: Value of the 13th observation
Step-by-step solution:
1. We know that the formula for calculating the mean of a data set is:
Mean = (Sum of all observations) / (Number of observations)
2. Using this formula, we can write two equations for the given information:
19.25 = (Sum of 12 observations) / 12 ... equation (1)
20 = (Sum of 13 observations) / 13 ... equation (2)
3. From equation (1), we can find the sum of the 12 observations:
Sum of 12 observations = 19.25 x 12 = 231
4. Substituting this value in equation (2), we get:
20 = (231 + 13th observation) / 13
Multiplying both sides by 13, we get:
260 = 231 + 13th observation
Subtracting 231 from both sides, we get:
13th observation = 29
Therefore, the value of the 13th observation is 29.
Mean of the new data set with 13 observations = 20
To find: Value of the 13th observation
Step-by-step solution:
1. We know that the formula for calculating the mean of a data set is:
Mean = (Sum of all observations) / (Number of observations)
2. Using this formula, we can write two equations for the given information:
19.25 = (Sum of 12 observations) / 12 ... equation (1)
20 = (Sum of 13 observations) / 13 ... equation (2)
3. From equation (1), we can find the sum of the 12 observations:
Sum of 12 observations = 19.25 x 12 = 231
4. Substituting this value in equation (2), we get:
20 = (231 + 13th observation) / 13
Multiplying both sides by 13, we get:
260 = 231 + 13th observation
Subtracting 231 from both sides, we get:
13th observation = 29
Therefore, the value of the 13th observation is 29.
Modal class of the following distribution is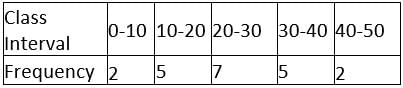
- a)10-20
- b)30-40
- c)20-30
- d)40-50
Correct answer is option 'C'. Can you explain this answer?
Modal class of the following distribution is
a)
10-20
b)
30-40
c)
20-30
d)
40-50
|
|
Megha Sharma answered |
Modal class means the time interval which has the highest frequency. Thus,in the table given,the highest frequency is 7 and it is the modal class of the following distribution.
The abscissa of the point of intersection of both types (less than & more than) of cumulative frequency curves help in finding- a)mean
- b)median
- c)mode
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The abscissa of the point of intersection of both types (less than & more than) of cumulative frequency curves help in finding
a)
mean
b)
median
c)
mode
d)
None of these
|
Aman kamat answered |
The abscissa of the point of intersection of both types of cumulative frequency curves helps in finding the median.
The median is the middle value in a dataset, and it divides the dataset into two equal parts. When we plot the cumulative frequency curve, we can find the median by finding the point of intersection of the two types of curves.
The point of intersection of the less than and more than cumulative frequency curves represents the median value. This is because at this point, half of the observations are below this value, and half of the observations are above this value.
The abscissa of the point of intersection does not help in finding the mean or mode. The mean is calculated by summing up all the observations and dividing by the number of observations. The mode is the value that appears most frequently in a dataset.
Therefore, the correct answer is (b) median.
The median is the middle value in a dataset, and it divides the dataset into two equal parts. When we plot the cumulative frequency curve, we can find the median by finding the point of intersection of the two types of curves.
The point of intersection of the less than and more than cumulative frequency curves represents the median value. This is because at this point, half of the observations are below this value, and half of the observations are above this value.
The abscissa of the point of intersection does not help in finding the mean or mode. The mean is calculated by summing up all the observations and dividing by the number of observations. The mode is the value that appears most frequently in a dataset.
Therefore, the correct answer is (b) median.
If the mean of frequency distribution is 7.5 and ∑fi xi = 120 + 3k, ∑fi = 30, then k is equal to:- a)40
- b)35
- c)50
- d)45
Correct answer is option 'B'. Can you explain this answer?
If the mean of frequency distribution is 7.5 and ∑fi xi = 120 + 3k, ∑fi = 30, then k is equal to:
a)
40
b)
35
c)
50
d)
45
|
|
Kds Coaching answered |
As per the given question,
Xmean = ∑fi xi /∑fi
7.5 = (120+3k)/30
225 = 120+3k
3k = 225-120
3k= 105
k=35
In the formula for finding the mean of a grouped frequency distribution, ui =
- a)
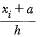
- b)h(xi - a)
- c)
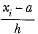
- d)
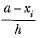
Correct answer is option 'C'. Can you explain this answer?
In the formula for finding the mean of a grouped frequency distribution, ui =
a)
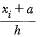
b)
h(xi - a)
c)
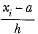
d)
|
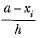
Kamna Science Academy answered |
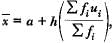this is step deviation formula used for finding mean
Choose the correct answer from the given four options : In the formula
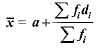for finding the mean of grouped data 
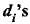are deviation from a of- a)lower limits of the classes
- b)upper limits of the classes
- c)mid-points of the classes
- d)frequencies of the class marks
Correct answer is option 'C'. Can you explain this answer?
Choose the correct answer from the given four options : In the formula
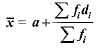for finding the mean of grouped data 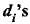are deviation from a of
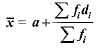for finding the mean of grouped data 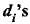are deviation from a ofa)
lower limits of the classes
b)
upper limits of the classes
c)
mid-points of the classes
d)
frequencies of the class marks
|
Manita Sh8arma Sh8arma answered |
Correct answer is 'c'
) of a frequency distribution is 45. If the value of 
= 20 then the value of 
is:
While computing mean of grouped data, we assume that the frequencies are- a)evenly distributed over all the classes
- b)centred at the classmarks of the classes
- c)centred at the upper limits of the classes
- d)centred at the lower limits of the classes
Correct answer is option 'B'. Can you explain this answer?
While computing mean of grouped data, we assume that the frequencies are
a)
evenly distributed over all the classes
b)
centred at the classmarks of the classes
c)
centred at the upper limits of the classes
d)
centred at the lower limits of the classes
|
Devika Dasgupta answered |
Understanding the Mean of Grouped Data
When calculating the mean of grouped data, it is essential to understand the assumptions made about the distribution of frequencies across the classes.
Assumption of Frequency Distribution
- When we compute the mean, we assume that the frequencies are distributed evenly within each class.
- However, this distribution is centered around the class marks, which are the midpoints of each class interval.
What are Class Marks?
- Class marks are calculated as the average of the upper and lower limits of the class.
- For example, if a class interval is 10-20, the class mark would be (10 + 20) / 2 = 15.
Why Centered at Class Marks?
- Centering at the class marks allows us to represent the entire frequency of that class with a single value, simplifying calculations.
- This assumption helps in obtaining a more accurate mean, as it accounts for the distribution of data within each interval.
Implications of Incorrect Assumptions
- If we were to center the frequencies at the upper or lower limits, we would misrepresent the data, leading to inaccuracies in the computed mean.
- Similarly, assuming frequencies are evenly distributed across all classes without using class marks would yield a skewed mean.
Conclusion
- Thus, in the calculation of the mean for grouped data, it is crucial to center the frequencies at the class marks to achieve a representative and accurate measure of central tendency. This ensures better statistical analysis and interpretation of the data.
When calculating the mean of grouped data, it is essential to understand the assumptions made about the distribution of frequencies across the classes.
Assumption of Frequency Distribution
- When we compute the mean, we assume that the frequencies are distributed evenly within each class.
- However, this distribution is centered around the class marks, which are the midpoints of each class interval.
What are Class Marks?
- Class marks are calculated as the average of the upper and lower limits of the class.
- For example, if a class interval is 10-20, the class mark would be (10 + 20) / 2 = 15.
Why Centered at Class Marks?
- Centering at the class marks allows us to represent the entire frequency of that class with a single value, simplifying calculations.
- This assumption helps in obtaining a more accurate mean, as it accounts for the distribution of data within each interval.
Implications of Incorrect Assumptions
- If we were to center the frequencies at the upper or lower limits, we would misrepresent the data, leading to inaccuracies in the computed mean.
- Similarly, assuming frequencies are evenly distributed across all classes without using class marks would yield a skewed mean.
Conclusion
- Thus, in the calculation of the mean for grouped data, it is crucial to center the frequencies at the class marks to achieve a representative and accurate measure of central tendency. This ensures better statistical analysis and interpretation of the data.
The runs scored by a batsman in 35 different matches are given below:
The number of matches in which the batsman scored less than 60 runs are- a)16
- b)24
- c)8
- d)19
Correct answer is option 'B'. Can you explain this answer?
The runs scored by a batsman in 35 different matches are given below:
The number of matches in which the batsman scored less than 60 runs are
The number of matches in which the batsman scored less than 60 runs are
a)
16
b)
24
c)
8
d)
19
|
|
Kds Coaching answered |
We need to find the number of matches in which the batsman scored less than 60 runs.
Step 1: Identify the relevant class intervals
The batsman scored less than 60 runs in the following class intervals:
- 0–15 (Frequency = 5)
- 15–30 (Frequency = 7)
- 30–45 (Frequency = 4)
- 45–60 (Frequency = 8)
Step 2: Sum the frequencies
Total number of matches where runs scored < 60:
= 5 + 7 + 4 + 8
= 24 matches
= 5 + 7 + 4 + 8
= 24 matches
Final Answer:
The number of matches in which the batsman scored less than 60 runs is 24.
Chapter doubts & questions for Statistics - Mathematics Class 10 (Maharashtra SSC Board) 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Statistics - Mathematics Class 10 (Maharashtra SSC Board) in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Mathematics Class 10 (Maharashtra SSC Board)
26 videos|208 docs|38 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup