All Exams >
Class 10 >
Mathematics Class 10 (Maharashtra SSC Board) >
All Questions
All questions of Trigonometry for Class 10 Exam
If tan A = 3/2, then the value of cos A is- a)
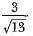
- b)
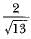
- c)2/3
- d)
Correct answer is option 'B'. Can you explain this answer?
If tan A = 3/2, then the value of cos A is
a)
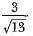
b)
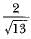
c)
2/3
d)
|
EduRev Class 10 answered |
Tanθ = Perpendicular / Base
We are given that TanA = 3/2
On comparing
Perpendicular = 3
Base = 2
To fing hypotenuse
Hypotenuse2 = Perpendicular2 + Base2
Hypotenuse2 = 32 + 22
Hypotenuse =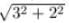
Hypotenuse = 3.6
We are given that TanA = 3/2
On comparing
Perpendicular = 3
Base = 2
To fing hypotenuse
Hypotenuse2 = Perpendicular2 + Base2
Hypotenuse2 = 32 + 22
Hypotenuse =
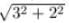
Hypotenuse = 3.6
Cosθ = Base / Hypotenuse
CosA = 2 / 3.6
Hence the value of Cos A is 2/3.6=2/√13
CosA = 2 / 3.6
Hence the value of Cos A is 2/3.6=2/√13
If tan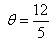 
, then 
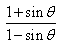is equal to- a)24
- b)12/13
- c)25
- d)9
Correct answer is option 'C'. Can you explain this answer?
If tan 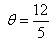, then 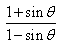is equal to
, then is equal toa)
24
b)
12/13
c)
25
d)
9
|
Vp Classes answered |
tanθ = 12/5
so sinθ = 12/13
so
(1 + 12/13)/(1-12/13)
= 25/1 = 25
The value of (sin 30° + cos 30°) - (sin 60° + cos 60°) is- a)-1
- b)0
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
The value of (sin 30° + cos 30°) - (sin 60° + cos 60°) is
a)
-1
b)
0
c)
1
d)
2
|
Ritu Saxena answered |
sin 30° = 1/2,
cos 30°=√3/2,
sin 60°=√3/2,
cos 60°=1/2,
By putting the value of sin 30°, cos 30°, sin 60° and cos 60° in equation
cos 30°=√3/2,
sin 60°=√3/2,
cos 60°=1/2,
By putting the value of sin 30°, cos 30°, sin 60° and cos 60° in equation
We get=
(sin30°+cos30°)-(sin60°+cos60°)=(1/2+√3/2)-(√3/2+1/2)
=0
(sin30°+cos30°)-(sin60°+cos60°)=(1/2+√3/2)-(√3/2+1/2)
=0
The value of (sin 45° + cos 45°) is- a)1/√2
- b)√2
- c)√3/2
- d)1
Correct answer is option 'B'. Can you explain this answer?
The value of (sin 45° + cos 45°) is
a)
1/√2
b)
√2
c)
√3/2
d)
1
|
Krishna Iyer answered |
sin 45° + cos 45°
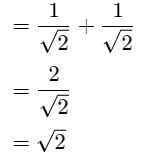
Hence, the answer is = √2
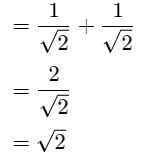
Hence, the answer is = √2
Can you explain the answer of this question below:If 7sin2x + 3cos2x = 4 then , secx + cosecx =- A:
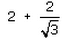
- B:
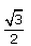
- C:
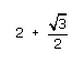
- D:
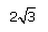
The answer is a.
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
A:
B:
C:
D:
|
Gunjan Lakhani answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=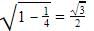
Sec x= 1/cos x=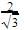
Cosec x + sec x=2+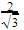
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
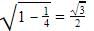
Sec x= 1/cos x=
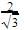
Cosec x + sec x=2+
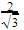
If tan θ = a/b then the value of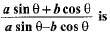 
- a)
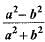
- b)
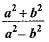
- c)
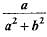
- d)
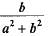
Correct answer is option 'B'. Can you explain this answer?
If tan θ = a/b then the value of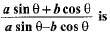
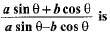
a)
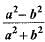
b)
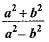
c)
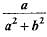
d)
|
|
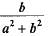
Vp Classes answered |
Let,angle= θ
(asinθ + bcosθ)/(asinθ - bcosθ)
Dividing both numerator and denominator from cosθ
We get,
atanθ +b/atanθ - b
= ( a.a/b + b) /(a.a/b - b) =(a²/b +b)/(a²/b - b)
=(a² + b²/a²- b²)
(asinθ + bcosθ)/(asinθ - bcosθ)
Dividing both numerator and denominator from cosθ
We get,
atanθ +b/atanθ - b
= ( a.a/b + b) /(a.a/b - b) =(a²/b +b)/(a²/b - b)
=(a² + b²/a²- b²)
If 6cotθ + 2cosecθ = cotθ + 5cosecθ, then cosθ is- a)4/5
- b)5/3
- c)3/5
- d)5/4
Correct answer is option 'C'. Can you explain this answer?
If 6cotθ + 2cosecθ = cotθ + 5cosecθ, then cosθ is
a)
4/5
b)
5/3
c)
3/5
d)
5/4
|
|
Raghav Bansal answered |
6cot+2cosec=cot+5cosec
6cot-cot=5cosec-2cosec
5cot=3cosec
5cos/sin=3/sin
cos=3/5
6cot-cot=5cosec-2cosec
5cot=3cosec
5cos/sin=3/sin
cos=3/5
Match the Columns:
- a)1 - A, 2 - C, 3 - B
- b)1 - B, 2 - C, 3 - A
- c)1 - B, 2 - C, 3 - D
- d)1 - D , 2 - B , 3 - A
Correct answer is option 'B'. Can you explain this answer?
Match the Columns:
a)
1 - A, 2 - C, 3 - B
b)
1 - B, 2 - C, 3 - A
c)
1 - B, 2 - C, 3 - D
d)
1 - D , 2 - B , 3 - A
|
|
Krishna Iyer answered |
Correct Answer :- b
Explanation : If θ is one of the acute angles in a triangle, then the sine of theta is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side.
9 sec2 A - 9tan2 A is equal to- a)1
- b)9
- c)8
- d)0
Correct answer is option 'B'. Can you explain this answer?
9 sec2 A - 9tan2 A is equal to
a)
1
b)
9
c)
8
d)
0
|
|
Kiran Mehta answered |
9 sec2 A - 9 tan2 A
= 9( sec2 A - tan2 A)
= 9 × 1
= 9
= 9( sec2 A - tan2 A)
= 9 × 1
= 9
Ratios of sides of a right triangle with respect to its acute angles are known as- a)trigonometric identities
- b)trigonometry
- c)trigonometric ratios of the angles
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Ratios of sides of a right triangle with respect to its acute angles are known as
a)
trigonometric identities
b)
trigonometry
c)
trigonometric ratios of the angles
d)
none of these
|
Ishan Choudhury answered |
The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle.
If 3 cot θ = 2, then the value of tan θ- a)2/3
- b)3/2
- c)
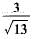
- d)
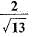
Correct answer is option 'B'. Can you explain this answer?
If 3 cot θ = 2, then the value of tan θ
a)
2/3
b)
3/2
c)
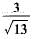
d)
|
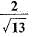
Hrishikesh Choudhary answered |
3cot theta =2
=> cot theta = 2/3
=> 1/tan theta =2/3
=>. tan theta = 3/2
hence, the answer is tan theta =3/2
If 7sin2x + 3cos2x = 4 then , secx + cosecx =- a)
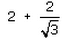
- b)
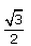
- c)
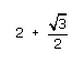
- d)
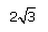
Correct answer is 'A'. Can you explain this answer?
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
a)
b)
c)
d)
|
Naina Sharma answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=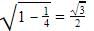
Sec x= 1/cos x=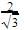
Cosec x + sec x=2+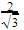
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
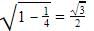
Sec x= 1/cos x=
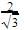
Cosec x + sec x=2+
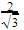
Read the following text and answer the following question on the basis of the same:Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.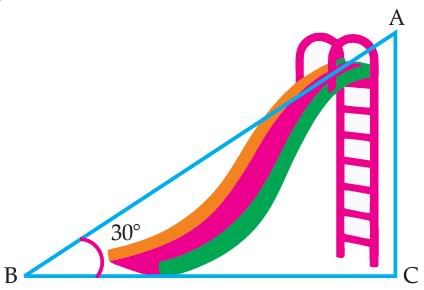
Q. The value of sin2 30° + cos2 60° is: - a)1 / 4
- b)1 / 2
- c)3 / 4
- d)3 / 2
Correct answer is option 'B'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
Q. The value of sin2 30° + cos2 60° is:
a)
1 / 4
b)
1 / 2
c)
3 / 4
d)
3 / 2
|
|
Ishan Choudhury answered |
Sin2 30° + cos2 60°
= (1 / 2)2 + (1 / 2)2
= 1 / 4 + 1 / 4
= 2 / 4 = 1 / 2
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
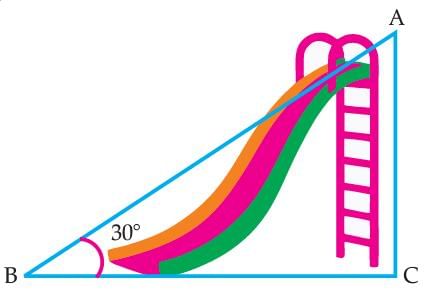Q. The distance of AB is :
- a)8 m
- b)6 m
- c)5 m
- d)10 m
Correct answer is option 'A'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
Q. The distance of AB is :
a)
8 m
b)
6 m
c)
5 m
d)
10 m
|
Avinash Patel answered |
We have,
∠B = 30° and AC = 4 m
sinθ=p/h or perpendicular/hypotenuse [perpendicular = side directly in front of θ ]
Then, sin 30° = AC / AB
⇒ 1 / 2 = 4 / AB
⇒ AB = 8 m.
Read the following text and answer the following question on the basis of the same:'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.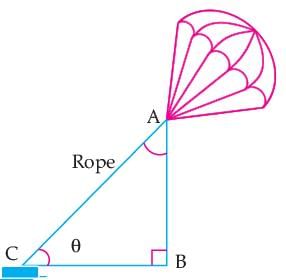
Q. What should be the length of the rope of the kite sail in order to pull the ship at the angle θ and be at a vertical height of 200 m?- a)400 m
- b)300 m
- c)100 m
- d)200 m
Correct answer is option 'A'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
Q. What should be the length of the rope of the kite sail in order to pull the ship at the angle θ and be at a vertical height of 200 m?
a)
400 m
b)
300 m
c)
100 m
d)
200 m
|
|
Rohit Sharma answered |
In ΔABC, we have
θ = 30°, AB = 200 m
Then, sin 30° = Perpendicular / Hypotenuse
= AB / AC
⇒ 1 / 2 = 200 / AC
⇒ AC = 400 m.
Read the following text and answer the following question on the basis of the same:'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.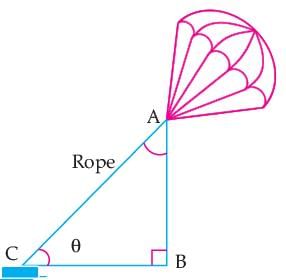
Q. If cos A = 1/ 2 , then the value of 9 cot2 A – 1 is:- a)1
- b)3
- c)2
- d)4
Correct answer is option 'C'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
Q. If cos A = 1/ 2 , then the value of 9 cot2 A – 1 is:
a)
1
b)
3
c)
2
d)
4
|
|
Naina Sharma answered |
Given, cos A = 1/ 2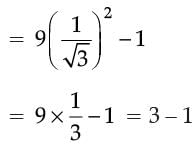
⇒ cos A = cos 60°
⇒ A = 60°
Then, 9 cot2 A – 1 = 9(cot 60°)2 – 1
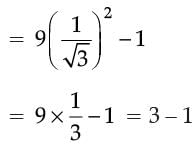
= 2
Read the following text and answer the following question on the basis of the same:Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.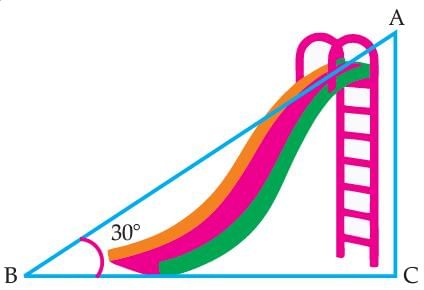
Q. If cos A = 1 / 2 , then the value of 12 cot2 A – 2 is:- a)5
- b)4
- c)3
- d)2
Correct answer is option 'D'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
Q. If cos A = 1 / 2 , then the value of 12 cot2 A – 2 is:
a)
5
b)
4
c)
3
d)
2
|
|
Kiran Mehta answered |
Cos A = 1 / 2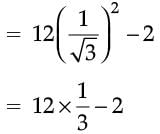
⇒ cos A = cos 60°
⇒ A = 60°
Then 12 cot2 A – 2 = 12(cot 60°) – 2
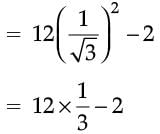
= 4 – 2 = 2.
The value of sin2 30° - cos2 30° is- a)-1/2
- b)
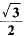
- c)3/2
- d)2/3
Correct answer is option 'A'. Can you explain this answer?
The value of sin2 30° - cos2 30° is
a)
-1/2
b)
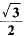
c)
3/2
d)
2/3
|
Kamna Science Academy answered |
Solution:
We know, sin 30° = 1/2 and cos 30° = √3/2.
Therefore, sin2 30° - cos2 30° = (1/2)2 - (√3/2)2
= 1/4 - 3/4
= -1/2
If cos X = a/b, then sin X is equal to:(- a)(b2-a2)/b
- b)(b-a)/b
- c)√(b2-a2)/b
- d)√(b-a)/b
Correct answer is option 'C'. Can you explain this answer?
If cos X = a/b, then sin X is equal to:(
a)
(b2-a2)/b
b)
(b-a)/b
c)
√(b2-a2)/b
d)
√(b-a)/b
|
Kds Coaching answered |
Answer: (c) √(b2-a2)/b
Explanation: cos X = a/b
By trigonometry identities, we know that:
sin2X + cos2X = 1
sin2X = 1 – cos2X = 1-(a/b)2
sin X = √(b2-a2)/b
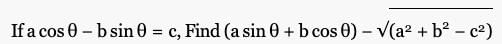
- a)0
- b)-ab
- c)c
- d)-c2
Correct answer is option 'A'. Can you explain this answer?
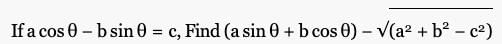
a)
0
b)
-ab
c)
c
d)
-c2
|
|
Kds Coaching answered |
We have,
a cos θ – b sin θ = c
a cos θ – b sin θ = c
Squaring both sides
⇒ a²cos²θ + b²sin²θ – 2ab sin θ cos θ = c²
⇒ a² (1 – sin²θ) + b² (1 – cos²θ) – 2ab sin θ cos θ = c²
⇒ a² – a²sin²θ + b² – b²cos²θ – 2ab sin θ cos θ = c²
⇒ a² + b² – c² = a²sin²θ + b²cos²θ + 2ab cos θ sin θ
⇒ a² + b² – c² = (a sin θ + b cos θ)²
⇒ (a sin θ + b cos θ) = ±√(a² + b² – c²) → (1)
⇒ a²cos²θ + b²sin²θ – 2ab sin θ cos θ = c²
⇒ a² (1 – sin²θ) + b² (1 – cos²θ) – 2ab sin θ cos θ = c²
⇒ a² – a²sin²θ + b² – b²cos²θ – 2ab sin θ cos θ = c²
⇒ a² + b² – c² = a²sin²θ + b²cos²θ + 2ab cos θ sin θ
⇒ a² + b² – c² = (a sin θ + b cos θ)²
⇒ (a sin θ + b cos θ) = ±√(a² + b² – c²) → (1)
So
(a sin θ + b cos θ) – √(a² + b² – c²) = 0
(a sin θ + b cos θ) – √(a² + b² – c²) = 0
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
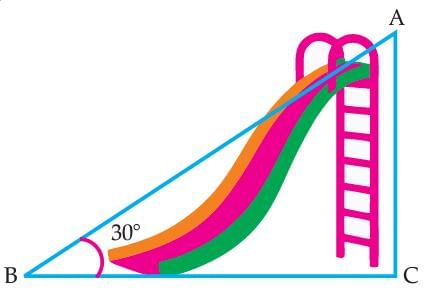Q. In the given figure, if AB + BC = 25 cm and AC = 5 cm, then the value of BC is:
- a)25 cm
- b)15 cm
- c)10 cm
- d)12 cm
Correct answer is option 'D'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
Q. In the given figure, if AB + BC = 25 cm and AC = 5 cm, then the value of BC is:
a)
25 cm
b)
15 cm
c)
10 cm
d)
12 cm
|
Vivek Rana answered |
We have,
∠C = 90°
AB + BC = 25 cm and AC = 5 cm
Let BC be x cm, then AB = (25 – x) cm
By using Pythagoras theorem,
AB2 = BC2 + AC2
⇒ (25 – x2) = x2 + (5)2
⇒ 625 – 50x + x2 = x2 + 25
⇒ 50x = 600
⇒ x = 600 / 50 = 12
Hence, BC = 12 cm
Read the following text and answer the following question on the basis of the same:Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.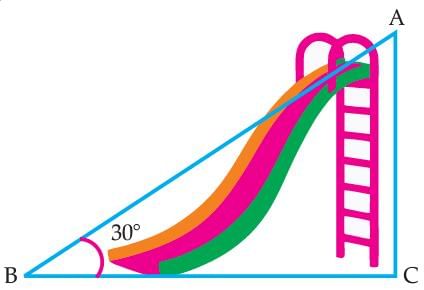
Q. In the given figure, the value of (sin C × cos A) is:- a)1 / 3
- b)1/2
- c)1 / 4
- d)1 / 5
Correct answer is option 'B'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
Authority wants to construct a slide in a city park for children. The slide was to be constructed for children below the age of 12 years. Authority prefers the top of the slide at a height of 4 m above the ground and inclined at an angle of 30° to the ground.
Q. In the given figure, the value of (sin C × cos A) is:
a)
1 / 3
b)
1/2
c)
1 / 4
d)
1 / 5
|
|
Kds Coaching answered |
Read the following text and answer the following question on the basis of the same:'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.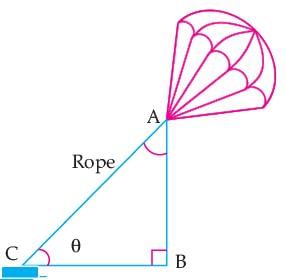
Q. In the given figure, if tan θ = cot (30° + θ), where θ and 30° + θ are acute angles, then the value of θ is: - a)45°
- b)30°
- c)60°
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
Q. In the given figure, if tan θ = cot (30° + θ), where θ and 30° + θ are acute angles, then the value of θ is:
a)
45°
b)
30°
c)
60°
d)
None of these
|
|
Aditya Shah answered |
Given, tan θ = cot(30° + θ)
= tan[90° – (30° + θ)]
= tan(90° – 30° – θ)
⇒ tan θ = tan(60° – θ)
⇒ θ = 60° – θ
⇒ 2θ = 60°
⇒ θ = 30°.
Read the following text and answer the following question on the basis of the same:'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.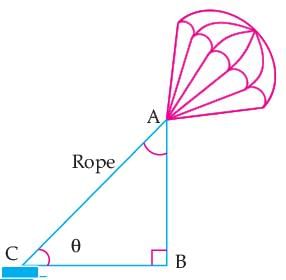
Q. The value of tan 30°. cot 60° is: - a)√3
- b)1 / √3
- c)1
- d)1 / 3
Correct answer is option 'D'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
Q. The value of tan 30°. cot 60° is:
a)
√3
b)
1 / √3
c)
1
d)
1 / 3
|
|
Ishan Choudhury answered |
Tan 30° × cot 60°
= 1 / √3 x 1 / √3
= 1 / 3.
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively. Where AB=200m and AC=400m
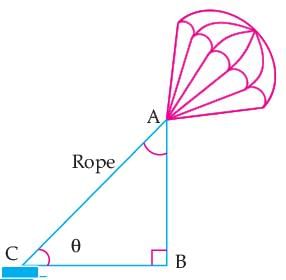Q. In the given figure, the value of (sin C + cos A) is:
- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
'Skysails' is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively. Where AB=200m and AC=400m
Q. In the given figure, the value of (sin C + cos A) is:
a)
1
b)
2
c)
3
d)
4
|
|
Naina Sharma answered |
We have,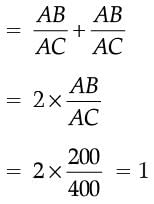
AB = 200 m and AC = 400 m Proved in Q.3]
Then, sin C + cos A
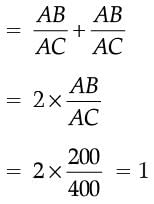
If sin A + sin2A = 1, then the value of the expression (cos2A + cos4A) is- a)1
- b)1/2
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
If sin A + sin2A = 1, then the value of the expression (cos2A + cos4A) is
a)
1
b)
1/2
c)
2
d)
3
|
|
Kds Coaching answered |
sin A + sin2A = 1
sin A = 1 – sin2A
sin A = cos2A {since sin2θ + cos2θ = 1}
Squaring on both sides,
sin2A = (cos2A)2
1 – cos2A = cos4A
⇒ cos2A + cos4A = 1
Chapter doubts & questions for Trigonometry - Mathematics Class 10 (Maharashtra SSC Board) 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Trigonometry - Mathematics Class 10 (Maharashtra SSC Board) in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Mathematics Class 10 (Maharashtra SSC Board)
26 videos|208 docs|38 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup